Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Сечения тетраэдра

Содержание

Взаимное расположение плоскости и многогранникаbcdaa. Нет точек пересеченияb. Одна точка пересеченияc. Пересечением является отрезокd. Пересечением является плоскость
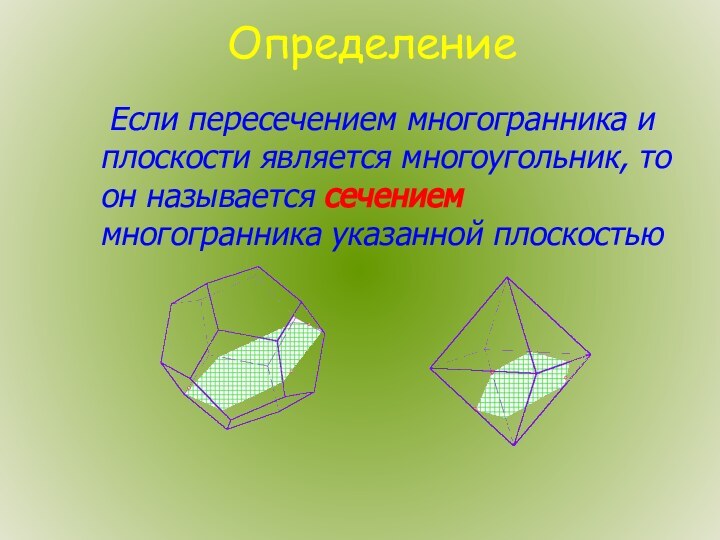
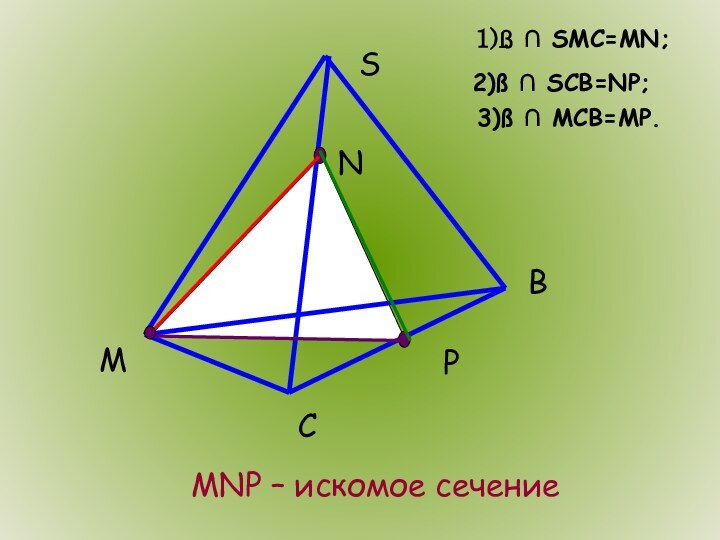
Сечения тетраэдра Взаимное расположение плоскости и многогранникаbcdaa. Нет точек пересеченияb. Одна точка пересеченияc. Пересечением Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью МЕТОД СЛЕДОВЗАДАЧА №1Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через точки 1)ß ∩ SMC=MN;2)ß ∩ SCB=NP;3)ß ∩ MCB=MP.MNP – искомое сечение МЕТОД СЛЕДОВЗАДАЧА №2Дан тетраэдр SMCB. 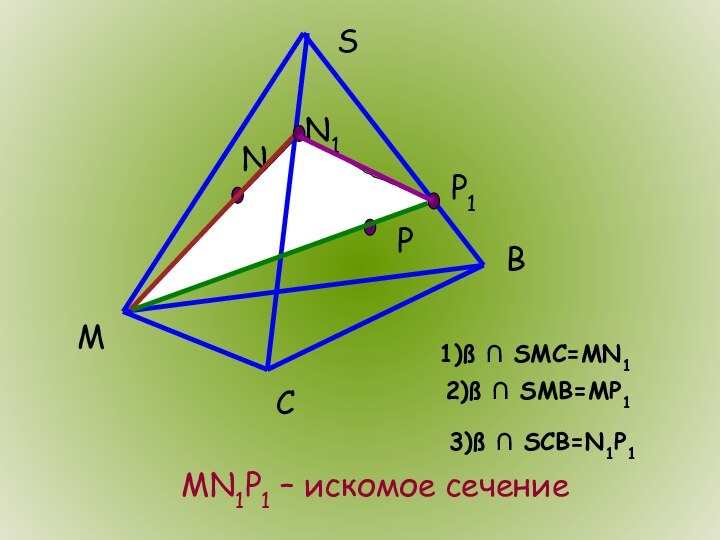Постройте сечение тетраэдра плоскостью, проходящей через точки SBMCNPN11)ß ∩ SMC=MN1P12)ß ∩ SMB=MP13)ß ∩ SCB=N1P1MN1P1 – искомое сечение МЕТОД СЛЕДОВЗАДАЧА №3Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через точки ADBCNPM1)ß ∩ ABC=MN2)ß ∩ ABD=NPF3)NP ∩ BD=F4) ß ∩ BCD=MKK5) ß ∩ ACD=KPMNPK – искомое сечение
Слайды презентации

Слайд 2 Взаимное расположение плоскости и многогранника
b
c
d
a

a. Нет точек пересечения
b.

Взаимное расположение плоскости и многогранникаbcdaa. Нет точек пересеченияb. Одна точка пересеченияc.

Одна точка пересечения
c. Пересечением является отрезок
d. Пересечением
является плоскость

Слайд 3 Определение
Если пересечением многогранника и плоскости является многоугольник, то

Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью

он называется сечением многогранника указанной плоскостью

Слайд 4 МЕТОД СЛЕДОВ
ЗАДАЧА №1

Дан тетраэдр SMCB. Постройте сечение тетраэдра

МЕТОД СЛЕДОВЗАДАЧА №1Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через

плоскостью, проходящей через точки M, N, P.
Известно, что

N ∈ SC, P ∈BC

Слайд 5


1)ß ∩ SMC=MN;
2)ß ∩ SCB=NP;
3)ß ∩ MCB=MP.
MNP –

1)ß ∩ SMC=MN;2)ß ∩ SCB=NP;3)ß ∩ MCB=MP.MNP – искомое сечение

искомое сечение

Слайд 6 МЕТОД СЛЕДОВ
ЗАДАЧА №2

Дан тетраэдр SMCB. Постройте сечение тетраэдра

МЕТОД СЛЕДОВЗАДАЧА №2Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через

плоскостью, проходящей через точки M, N, P.
Известно, что

N ∈SMC
P∈MSB

Слайд 7
S
B
M
C
N


P
N1

1)ß ∩ SMC=MN1
P1
2)ß ∩ SMB=MP1


3)ß ∩ SCB=N1P1
MN1P1 –

SBMCNPN11)ß ∩ SMC=MN1P12)ß ∩ SMB=MP13)ß ∩ SCB=N1P1MN1P1 – искомое сечение

искомое сечение

Слайд 8 МЕТОД СЛЕДОВ
ЗАДАЧА №3

Дан тетраэдр SMCB. Постройте сечение тетраэдра

МЕТОД СЛЕДОВЗАДАЧА №3Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через

плоскостью, проходящей через точки M, N, P.
Известно, что

N ∈AB, P∈AD, M ∈BC
  • Имя файла: secheniya-tetraedra.pptx
  • Количество просмотров: 97
  • Количество скачиваний: 0
- Предыдущая Захист від клавіатурних шпигунів. (Лекція 1.2)
Следующая - Snezhinki-i-elka

Похожие презентации

Возникновение измерений в древности Возникновение измерений в древности 107
Вычитание чисел Вычитание чисел 90
Решение уравнений Решение уравнений 159
Дополнения к значениям тригонометрических функций Дополнения к значениям тригонометрических функций 94
Открытое мероприятие Праздник числа для 1 класса презентация урока для интерактивной доски по математике (1 класс) по теме Открытое мероприятие Праздник числа для 1 класса презентация урока для интерактивной доски по математике (1 класс) по теме 109
Расстояние между двумя точками. Масштаб Расстояние между двумя точками. Масштаб 111
Фотоотчет о неделе математики презентация к уроку по математике Фотоотчет о неделе математики презентация к уроку по математике 112
Презентация по математике на тему:Сложение и вычитание в пределах 100.Решение задач (2 класс) Презентация по математике на тему:Сложение и вычитание в пределах 100.Решение задач (2 класс) 146
Сложение и вычитание трехзначных чисел Сложение и вычитание трехзначных чисел 133
Дидактическая игра Сложение и вычитание круглых десятков Дидактическая игра Сложение и вычитание круглых десятков 32
prezentatsiya moskva dlya uroka prezentatsiya moskva dlya uroka 89
Презентация по математике на тему Длина окружности и площадь круга ( 6 класс) Презентация по математике на тему Длина окружности и площадь круга ( 6 класс) 219
Использование тригонометрической окружности при решении тригонометрический уравнений Использование тригонометрической окружности при решении тригонометрический уравнений 94
Решето Эратосфена Решето Эратосфена 88
Деление на десятичную дробь Деление на десятичную дробь 108
Призма Призма 132
Угол 7 класс Угол 7 класс 103
Презентация Мир геометрических фигур (многоугольники) презентация к уроку по математике (1 класс) Презентация Мир геометрических фигур (многоугольники) презентация к уроку по математике (1 класс) 116
Презентация Блоки Дьеныша презентация к уроку по математике (средняя группа) Презентация Блоки Дьеныша презентация к уроку по математике (средняя группа) 101
Презентация к уроку Новые мерки. Умножение презентация к уроку по математике (2 класс) по теме Презентация к уроку Новые мерки. Умножение презентация к уроку по математике (2 класс) по теме 110
Числа в народном творчестве Числа в народном творчестве 96
Сабак жоспары, презентациямен, Аралас сандарды азайту 5 сынып Сабак жоспары, презентациямен, Аралас сандарды азайту 5 сынып 178
Медианы, биссектрисы и высоты треугольника Медианы, биссектрисы и высоты треугольника 108
Размещения и сочетания Размещения и сочетания 118
Золотое сечение в архитектуре 9 класс Золотое сечение в архитектуре 9 класс 124
Математика повсюду Математика повсюду 110
Презентация-Танграм презентация по математике по теме Презентация-Танграм презентация по математике по теме 135
Презентация к уроку математики Длина. Сантиметр презентация к уроку по математике (1 класс) Презентация к уроку математики Длина. Сантиметр презентация к уроку по математике (1 класс) 89
Замысловатые маршруты и правила Эйлера Замысловатые маршруты и правила Эйлера 83
Умножение обыкновенных дробей Умножение обыкновенных дробей 103