- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многоугольники в природе. Паркеты из правильных многоугольников.
Содержание
- 2. Многоугольники в природе.В природе часто встречаются разнообразные
- 3. Примеры многоугольников в природе.Примерами правильных многоугольников в
- 4. Пчелиные соты.Пчелиные соты состоят из шестиугольников. Но
- 5. Снежинки.Снежинки могут иметь форму треугольника или шестиугольника.
- 6. Сложные молекулы углерода. Также примером многоугольников в природе могут служить некоторые сложные молекулы углерода.
- 7. Здание Пентагона. А вот еще один пример
- 8. Здание Пентагона
- 9. Паркеты из правильных многоугольниковВ математике паркетом называют
- 10. Скачать презентацию
- 11. Похожие презентации
Многоугольники в природе.В природе часто встречаются разнообразные правильные многоугольники. Это могут быть треугольники, четырехугольнике, пятиугольники и т.д. Виртуозно компонуя их, природа создала бесконечное множество сложных, удивительно красивых, легких, прочных и экономичных конструкций.








Слайд 3
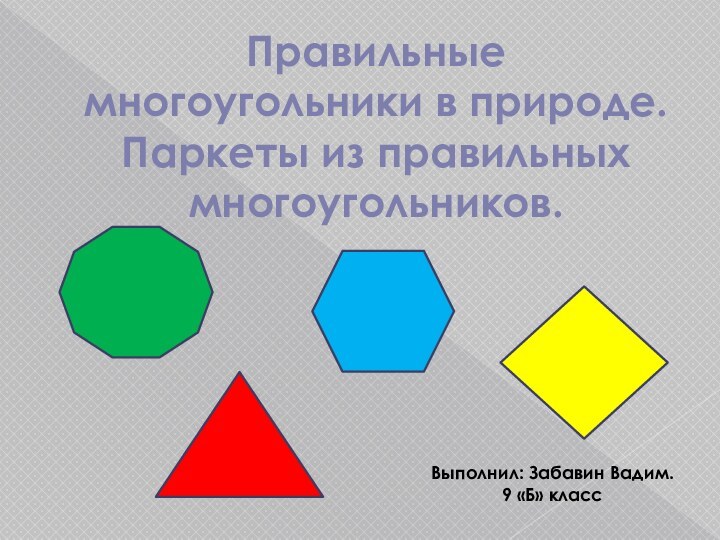
Примеры многоугольников в природе.
Примерами правильных многоугольников в природе
могут служить:
Пчелиные соты, снежинки и другие.
Рассмотрим их по подробней…
Слайд 4
Пчелиные соты.
Пчелиные соты состоят из шестиугольников. Но почему
пчелы «выбрали» для ячеек на сотах именно форму правильных
шестиугольников?Из правильных многоугольников с одинаковой площадью наименьший периметр у правильных шестиугольников. При такой «математической» работе пчёлы экономят 2% воска. Количество воска сэкономленного при постройке 54 ячеек, может быть использовано для постройки одной такой же ячейки. Стало быть, мудрые пчёлы экономят воск и время для постройки сот.
Слайд 5
Снежинки.
Снежинки могут иметь форму треугольника или шестиугольника. Но
почему только эти две формы?
Так получилось, что молекула воды
состоит из трех частиц – двух атомов водорода и одного атома кислорода. Поэтому при переходе частицы воды из жидкого состояния в твердое, ее молекула соединяется с другими молекулами воды, и образует только трех – или шестиугольную фигуру.
Слайд 6
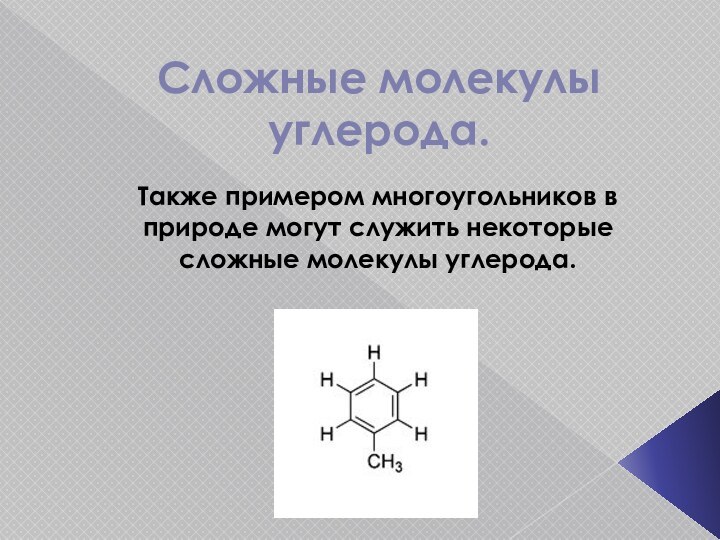
Сложные молекулы углерода.
Также примером многоугольников в природе
могут служить некоторые сложные молекулы углерода.
Слайд 7
Здание Пентагона.
А вот еще один пример многоугольников.
Но уже созданный не природой, а человеком. Это здание
Пентагона. Он имеет форму пятиугольника.Но почему здание Пентагона имеет такую форму?
Пятиугольную форму здания подсказал план местности, когда создавались эскизы проекта. В том месте проходило несколько дорог, которые пересекались под углом 108 градусов, а это и есть угол построения пятиугольника. Поэтому такая форма органично вписывалась в транспортную инфраструктуру, и проект был утвержден.
Слайд 9
Паркеты из правильных многоугольников
В математике паркетом называют «замощение»
плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты
были открыты пифагорейцами около 2500 лет тому назад.Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников, либо четыре квадрата, либо три правильных шестиугольника.