- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Осевая и центральная симметрии
Содержание
- 2. Что такое симметрия?Осевая симметрияПостроение осевой симметрииЦенральная симметрияПостроение центральной симметрииСимметрия в окружающем нас мире
- 3. В математике рассматрива-ются два вида симметрии: осевая
- 4. Осевая симметрияФигура называется симмет-ричной относительно прямой a,
- 5. Ось симметрии имеют плоские и пространственные
- 6. Построение осевой симметрииaM1MOдалееПроведём прямую a и от-метим
- 7. Задание№2.
- 8. Центральная симметрияЦентральная симметрия является ещё одним видом
- 9. Если внимательно рассмотреть данные орнаменты и фигуры,
- 10. Отметим на листе бумаги произ-вольные точки O
- 11. Задание № 4.
- 12. Симметрия в окружающем нас миреВзгляните на снежинку,
- 13. Скачать презентацию
- 14. Похожие презентации










Слайд 2
Что такое симметрия?
Осевая симметрия
Построение осевой симметрии
Ценральная симметрия
Построение центральной
симметрии
Слайд 3 В математике рассматрива-ются два вида симметрии: осевая и
центральная. Зеркальная сим-метрия считается одним из видов осевой. Различные
геомет-рические фигуры обладают сим-метрией. Наша с вами задача: определить, что называют осевой и центральной симметрией, научиться их различать и строить, определить фигуры, обладающие той или иной симметрией.назад
Слово «симметрия», как и многие другие математические термины, пришло к нам из Древней Греции. Оно, как и слово «гармония», означает «соразмерность», «наличие определённого порядка, закономер-ности в расположении частей».
Слайд 4
Осевая симметрия
Фигура называется симмет-ричной относительно прямой a, если
для каждой точки фигуры симметричная ей точка отно-сительно прямой
a также при-надлежит этой фигуре. Прямая a называется осью симметрии фигуры.далее
Рассмотрите данные фигуры. Каждая из них состоит как бы из двух полови-нок, одна из ко-торых является зеркальным отра-жением другой. Каждую из этих фигур можно сог-нуть «пополам» так, что эти поло-винки совпадут. Говорят, что эти фигуры симмет-ричны относи-тельно прямой – линии сгиба.
Слайд 5 Ось симметрии имеют плоские и пространственные фигуры.
Например:
Некоторые фигуры имеют не одну ось симметрии.
Задание№1.
Из данных фигур выберите те, которые имеют ось симметрии. Есть ли среди них такие, которые имеют более одной оси симметрии? На листе бумаги изображена «ёлочка». Концы её нижних «веток» обозначены буквами A и A1. Если перегнуть «ёлочку» по прямой l, то точки A и A1 совпадут. Если посмотреть на рисунок сверху, то точки A и A1 будут расположены на пер-пендикуляре к прямой l по разные стороны и на равных расстояниях от неё. Такие точки называют симмет-ричными относительно пря-мой l .
назад
Слайд 6
Построение осевой симметрии
a
M1
M
O
далее
Проведём прямую a и от-метим точку
M вне этой прямой.
Построим точку, симметричную данной, относительно прямой
a.1) Проведём через точку M пря-мую MO,перпендикулярную оси симметрии a.
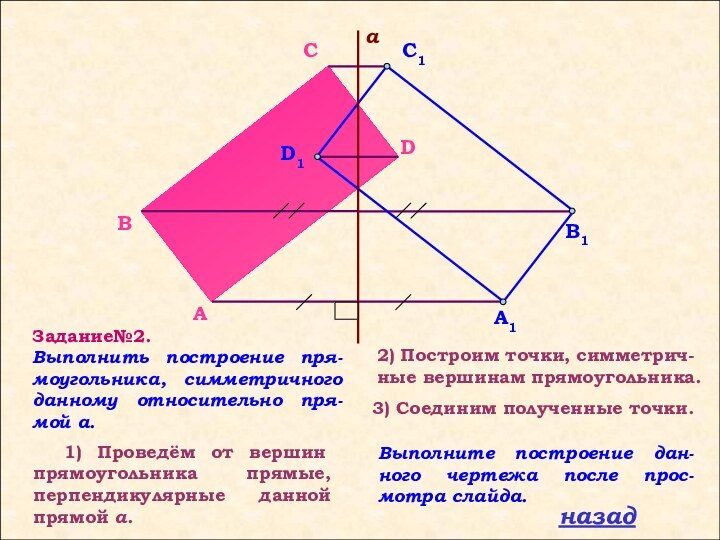
Слайд 7 Задание№2.
Выполнить построение пря-моугольника, симметричного данному относительно пря-мой
a. 1) Проведём от вершин прямоугольника прямые, перпендикулярные данной прямой a.
B
B1
a
A
C
D
A1
C1
D1
назад
Выполните построение дан-ного чертежа после прос-мотра слайда.
2) Построим точки, симметрич-ные вершинам прямоугольника.
3) Соединим полученные точки.
Слайд 8
Центральная симметрия
Центральная симметрия является ещё одним видом симметрии.
Фигура называется симметричной относительно точки O, если для каждой
точки фигуры симметричная ей точка относительно точки O также принадлежит этой фигуре. Точка O называется центром симметрии. Вы знаете, что существуют фигуры, которые имеют ось симметрии, а некоторые и не одну. Но фигура может иметь и центр симметрии. Точка является центром симмет-рии, если при повороте вокруг этой точки на 1800 фигура переходит сама в себя. Такие фигуры назы-ваются центрально-симмет-ричными.
далее
Слайд 9 Если внимательно рассмотреть данные орнаменты и фигуры, можно
заметить, что все они имеют центр симметрии.
Задание№3.
На рисунке изображены различные геометричес-кие фигуры. Выберите из них те, которые име-ют центр симметрии, и изобразите их в тет-ради. Отметьте центр симметрии и точки, симметричные отмечен-ным точкам.назад
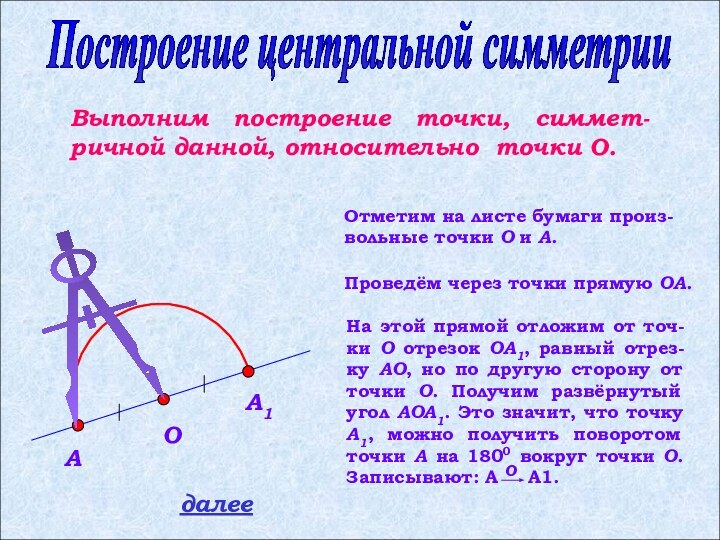
Слайд 10 Отметим на листе бумаги произ-вольные точки O и
A.
Проведём через точки прямую OA.
A1
A
O
Построение центральной симметрии
Выполним построение точки,
симмет-ричной данной, относительно точки O. далее
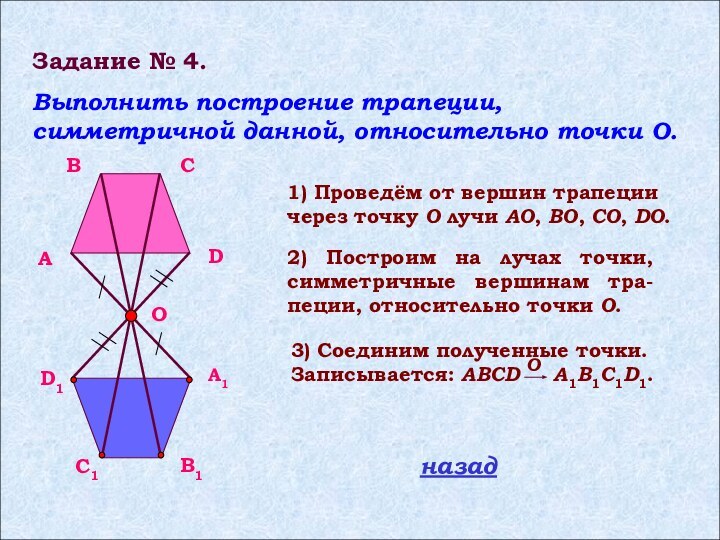
Слайд 11 Задание № 4.
Выполнить построение трапеции, симметричной данной, относительно точки O.
A
B
C
D
A1
B1
C1
D1
O
1) Проведём от вершин трапеции через точку O лучи AO, BO, CO, DO.
2) Построим на лучах точки, симметричные вершинам тра-пеции, относительно точки O.
назад
Слайд 12
Симметрия в окружающем нас мире
Взгляните на снежинку, бабочку,
морскую звезду, листья растений, паутинку – это лишь некоторые
про-явления симметрии в природе.Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии.
далее