- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Симметрия в пространстве
Содержание
- 2. цельНа примерах найти и показать симметрию как основу красоты в природе, технике, архитектуре и искусстве.
- 3. СОДЕРЖАНИЕСимметрияИстория симметрииВиды симметрииСимметрия в природеСимметрия в архитектуреСимметрия в техникеСимметрия на примере геометрической фигуры - октаэдр
- 4. Что такое симметрия?Симметрия – это неизменность при
- 5. История симметрииЕщё древние греки считали, что симметрия
- 6. ВИДЫ СИММЕТРИИЦентральная симметрияОсевая симметрияЗеркальная симметрия
- 7. Центральная симметрияЦентральной симметрией (иногда центра́льной инве́рсией) относительно точки O называют преобразование пространства, переводящее точку X в такую точку X′, что O — середина отрезка XX′.
- 8. Осевая симметрияСимметрия относительно прямой (или осевая симметрия)
- 9. Зеркальная симметрия Точки А и В называются симметричными относительно плоскости α (плоскость
- 10. С симметрией мы встречаемся везде – в
- 11. Симметрия в природеВ отличие от искусства или
- 12. Симметрия в природеПримеры трансляции подобия в природных
- 13. Симметрия в природеСложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии
- 14. Симметрия, созданная природой
- 15. симметрия в архитектуре"...быть прекрасным значит быть симметричным
- 16. симметрия в архитектуреАрхитектура - удивительная область человеческой
- 17. симметрия в архитектуреЭйфелева башняСобор Парижской Богоматери
- 18. симметрия в архитектуреМГУ
- 19. Симметрия в техникеБольшинство самых необходимых для нас
- 20. Симметрия в техникеБольшинство транспортных средств, от детской
- 21. Симметрия в техникеРазличные фигуры, чаще симметричные, используются для составления орнаментов в народном творчестве.
- 22. Пример интересной симметрииПальманова — город-крепость с населением
- 23. Пример интересной симметрииПозднее уже сами жители попытались
- 24. ОКТАЭДРОктаэдр — один из 5-ти выпуклых правильных многогранников.Октаэдр имеет
- 25. ОКТАЭДРЕсли длина ребра октаэдра равна а, то площадь
- 26. ОКТАЭДРКристаллы алмаза обычно имеют форму октаэдра. Алмаз (от греческого
- 27. ОКТАЭДРКак и все правильные многогранники, октаэдр обладает
- 28. Симметрия, проявляясь в самых различных объектах материального
- 29. Скачать презентацию
- 30. Похожие презентации
цельНа примерах найти и показать симметрию как основу красоты в природе, технике, архитектуре и искусстве.



























Слайд 2
цель
На примерах найти и показать симметрию как основу
красоты в природе, технике, архитектуре и искусстве.
Слайд 3
СОДЕРЖАНИЕ
Симметрия
История симметрии
Виды симметрии
Симметрия в природе
Симметрия в архитектуре
Симметрия в
технике
Симметрия на примере геометрической фигуры - октаэдр
Слайд 4
Что такое симметрия?
Симметрия – это неизменность при каких-либо
преобразованиях.
Это означает, что при определённых трансформациях, производимых с объектом,
тот не изменяется.
Слайд 5
История симметрии
Ещё древние греки считали, что симметрия –
это гармония, соразмерность.
А у древних народов, таких как шумеры
и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Слайд 7
Центральная симметрия
Центральной симметрией (иногда центра́льной инве́рсией) относительно точки O называют преобразование пространства,
переводящее точку X в такую точку X′, что O — середина отрезка XX′.
Слайд 8
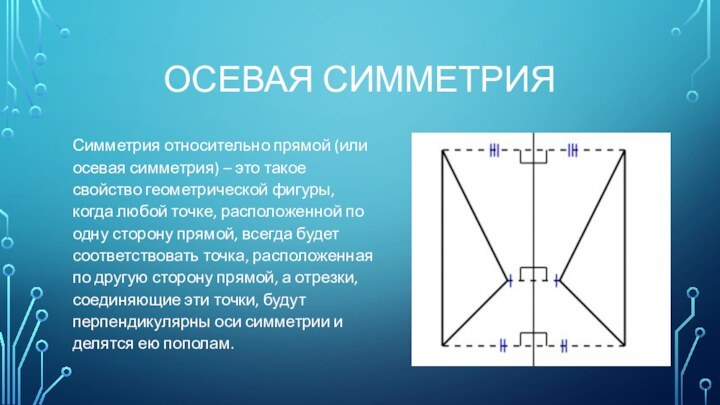
Осевая симметрия
Симметрия относительно прямой (или осевая симметрия) –
это такое свойство геометрической фигуры, когда любой точке, расположенной
по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.
Слайд 9
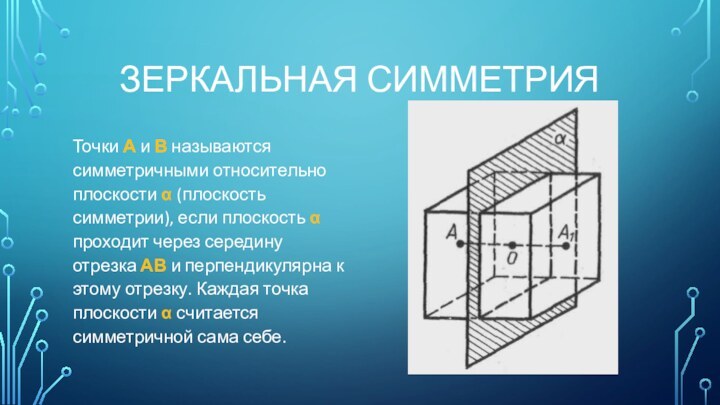
Зеркальная симметрия
Точки А и В называются симметричными относительно плоскости α (плоскость симметрии),
если плоскость α проходит через середину отрезка АВ и перпендикулярна к
этому отрезку. Каждая точка плоскости α считается симметричной сама себе.Слайд 10 С симметрией мы встречаемся везде – в природе,
технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и
кленовому листу, симметрию автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов.Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
Слайд 11
Симметрия в природе
В отличие от искусства или техники,
красота в природе не создаётся, а лишь фиксируется, выражается.
Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. К числу таких образов относятся некоторые кристаллы, многие растения.
Слайд 12
Симметрия в природе
Примеры трансляции подобия в природных формах.
Лист подчиняется принципу зеркальной симметрии с одновременным уменьшением элементов
(направленностью симметрии), цветок отличается соединением радиальной и спиральной (в трех измерениях) симметрии. Подобным же образом строятся динамично-симметричные формы раковин, листьев папоротника.
Слайд 13
Симметрия в природе
Сложные узоры на крыльях бабочки являются одним
из примеров двусторонней симметрии
Слайд 15
симметрия в архитектуре
"...быть прекрасным значит быть
симметричным и
соразмерным"
Платон
(древнегреческий философ, 428 – 348 г. до н.э.)
Симметричность
очень приятна глазу. Я часто любовалась и любуюсь листьями, цветами, птицами, животными или творениями человека: зданиями, техникой, - всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
Слайд 16
симметрия в архитектуре
Архитектура - удивительная область человеческой деятельности.
В ней тесно переплетены и строго уравновешены наука, техника,
искусство.Прошли века, но роль симметрии не изменилась.
Появляются новые строительные материалы, но математические основы законов красоты в архитектуре остаются неизменными. Одним из художественных средств, которые он использует, является композиция здания. От неё в первую очередь зависит впечатление, которое оставляет архитектурное сооружение.
В скульптуре основу композиции и изображения фигур составляет тоже теория пропорций. Использование симметрии в конструкции зданий, симметричных элементов в отделке, а также симметрично расположенные строения создают красоту и гармонию.
Слайд 19
Симметрия в технике
Большинство самых необходимых для нас предметов
— от книги, ложки, чайника и молотка до газовой
плиты, холодильника и пылесоса — тоже обладает симметрией.
Слайд 20
Симметрия в технике
Большинство транспортных средств, от детской коляски
до сверхзвукового реактивного воздушного лайнера, предназначенных для движения по
земной поверхности или параллельно ей, так же имеют осевую симметрию
Слайд 21
Симметрия в технике
Различные фигуры, чаще симметричные, используются для
составления орнаментов в народном творчестве.
Слайд 22
Пример интересной симметрии
Пальманова — город-крепость с населением около
5400 человек, расположенный на северо-востоке страны примерно в 25
км к югу от Удине, был заложен в конце XVI столетия, при непосредственной поддержке правительства Венецианской республики. Пальманова должна была стать образцом города-крепостиПальманова — симметричный город-крепость в Италии
Слайд 23
Пример интересной симметрии
Позднее уже сами жители попытались реализовать
утопическую идею, что симметрия реально помогает людям жить и
развиваться. Форма девятиугольной звезды была образована так, чтобы любой из девяти «углов» мог в случае атаки получить поддержку и помощь от соседнего «угла». В город можно было попасть через одни из трех ворот. Внутри город состоит из трех «колец-уровней».
Слайд 24
ОКТАЭДР
Октаэдр — один из 5-ти выпуклых правильных многогранников.
Октаэдр имеет 8
треугольных граней, 12 рёбер, 6 вершин, в каждой его
вершине сходятся 4 ребра.
Слайд 25
ОКТАЭДР
Если длина ребра октаэдра равна а, то площадь его
полной поверхности (S) и объём октаэдра (V) вычисляются по
формулам:
Слайд 26
ОКТАЭДР
Кристаллы алмаза обычно имеют форму октаэдра. Алмаз (от греческого adamas
– несокрушимый) – бесцветный или окрашенный кристалл с сильным
блеском в виде октаэдра. Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, ромбододекаэдров, реже — кубов или тетраэдров.
Слайд 27
ОКТАЭДР
Как и все правильные многогранники, октаэдр обладает симметрией.
Три
из 9 осей симметрии октаэдра проходят через противоположные вершины, шесть -
через середины ребер. Центр симметрии октаэдра - точка пересечения его осей симметрии.Три из 9 плоскостей симметрии проходят через каждые 4 вершины октаэдра, лежащие в одной плоскости.
Шесть плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер.
Слайд 28 Симметрия, проявляясь в самых различных объектах материального мира,
несомненно, отражает наиболее общие, наиболее фундаментальные его свойства. Поэтому исследование
симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.заключение