ней мелом разные фигуры, я вдруг был поражен мыслью:
почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?»Лев Николаевич Толстой
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Симметрия вокруг нас
Содержание
- 2. «Стоя перед черной доской и рисуя
- 4. План урокаТеоретический блиц-опросЗащита учебных проектовПодведение итогов работы над проектамиДомашнее задание
- 5. Симметрия…является той идеей, посредством которой человек на
- 6. Блиц-опросЧто понимается под движением? 2. Приведите примеры движений.
- 7. Иллюстрация какой симметрии представлена на рисунке?А)А’АПереносная→аБ) АА’600ПоворотнаяО
- 8. В)АОЦентральнаяГ)aОсеваяA’AA’
- 9. Д)Зеркальная
- 10. Защита проектов
- 11. Проект 1 группы: «Симметрия в алгебре».Проект подготовили:Гвоздева А.Каплун В.Ковальчук О.Онуфриенко А.Пономаренко К.Ковалева У.Маликов И.Курбанова А.
- 12. Симметрия в алгебре
- 14. Функция называется чётной, если справедливо равенство
- 15. Симметрические функции
- 17. Возвратные уравнения 3-й и 4-й степениМногочлены n-ой
- 18. 2x3+7x 2 +7x+2 = 02x3 +2+7x2
- 19. 6х4-35х3+62х2-35х+6х2=06х2-35х+62-35/х+6=06х2+6/х2-35х-35/х+62=06(х2+1/х2)-35(х+1/х)+62=0Х+1/х=z (х+1/х)2=z2Х2+2+1/х2=z2Х2+1/х2=z2-26(z2-2)-35z+62=06z2-12-35z+62=06z2-35z+50=0Д=b2-4ac=(-35)2-4*6*50= 1225-1200= 25Z1=5/2Z2= 10/3х+ 1/х=5/2
- 20. Системы уравнений второй степени.Система уравнений
- 21. Укажите симметричные многочлены:X3+4x2y+4xy2+y33x4-8x3y+3y4X5+Y52x4+7x3y+7xy3+2y4
- 22. Литература1. Виленкин Н.Я.Алгебра :издательство «Просвещение» Москва, 1968.2.
- 23. Проект 2 группы: Симметрия в архитектуре «Вдоль Кремлевской стены».Проект подготовили:Тихонова В.Вялых И.Гурина В.Швец С.Короткова В.Вельчев Н.
- 24. Вдоль Кремлевской стены
- 25. « Чувство симметрии и реальное стремление его
- 26. «Изучение археологических памятников показывает, что человечество на
- 27. Архитектурные стили готикабароккохай-текмодернклассицизмампирфутуризмконструктивизмэклектика
- 28. Маринкина башня
- 29. Грановитая башня
- 30. Ямская
- 31. Пятницкие ворота
- 32. Литература 1.Большаков М.В. Декор и орнамент
- 33. Проект 3 группы:«Симметрия в природе»Проект подготовили:Бугаёва Оксана,Пизикс Алёна,Кравченко Катя,Имерели Данил,Пизикс Андрей,Жигалов Саша,Трапезников Коля,Боровиков Саша,Конограев Максим,Гелеверя Вадик.
- 34. Симметрия в природе
- 35. Симметрия является важнейшим свойством природы. Поразительные по
- 36. Под симметрией у животных понимают соответствие в
- 37. В XX веке усилиями российских учёных -
- 38. У цветковых растений в большинстве проявляется радиальная
- 39. Симметрия у человекаТело человека построено по принципу двусторонней симметрии
- 40. Диссимметрия — это частично расстроенная симметрия,противоречивое единство
- 42. Антисимметрия – это сохранение одного свойства объекта и замена другого свойства на противоположное.
- 43. Асимметрия– это отсутствие
- 44. Асимметрия– это отсутствие
- 45. Литература Гильде В. Зеркальный мир. — М.:
- 46. Подведение итогаНа вопрос «Чему удалось научиться в ходе работы над проектом?» Школьники отвечают:
- 47. Скачать презентацию
- 48. Похожие презентации
«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно
Слайд 3
Цели урока:
Выявить значение принципа симметрии в
алгебре.
Выявить архитектурные
стили, представленные в Коломне.
Научиться определять виды симметрии в природе.
Познакомиться с понятиями «асимметрия»,
«диссимметрия», «антисимметрия».
Ответить на вопросы:
1)Во всем ли в жизни симметрия?
2)Только ли симметрия является признаком
красоты?
Слайд 4
План урока
Теоретический блиц-опрос
Защита учебных проектов
Подведение итогов работы над
проектами
Домашнее задание
Слайд 5 Симметрия…является той идеей, посредством которой человек на протяжении
веков пытался постичь и создать порядок, красоту и совершенство. Г.
Вейль
Слайд 11
Проект 1 группы:
«Симметрия в алгебре».
Проект подготовили:
Гвоздева А.
Каплун
В.
Ковальчук О.
Онуфриенко А.
Пономаренко К.
Ковалева У.
Маликов И.
Курбанова А.
Слайд 14
Функция называется чётной, если справедливо равенство
График
чётной функции симметричен относительно оси
ординат . .
Функция
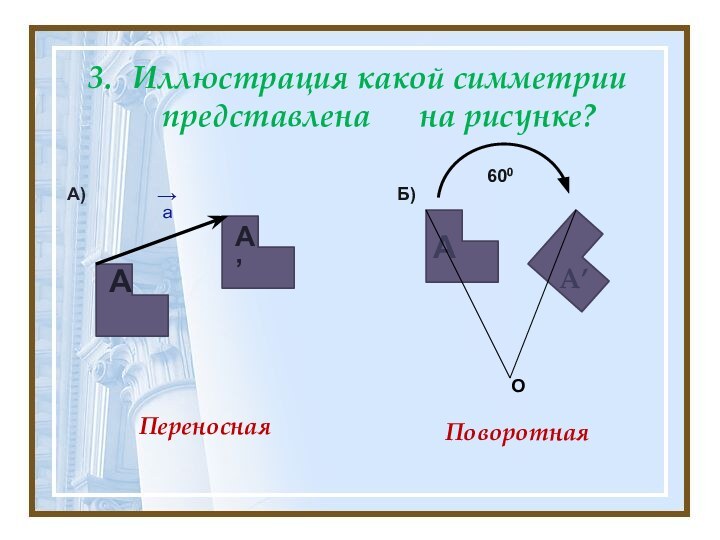
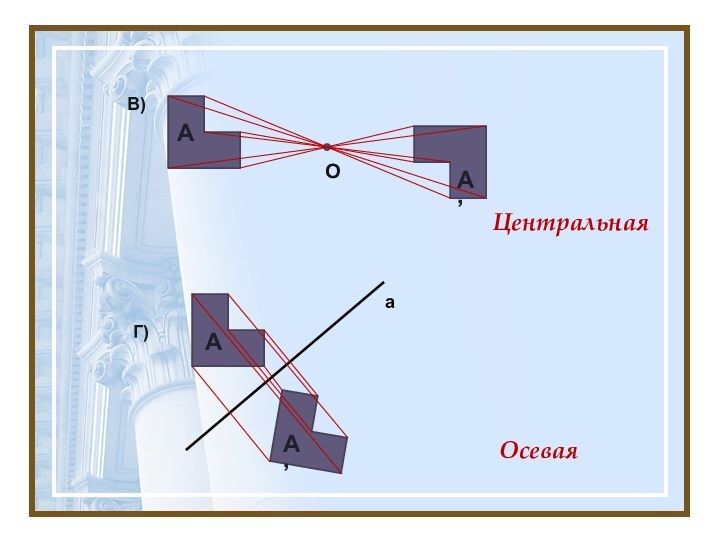
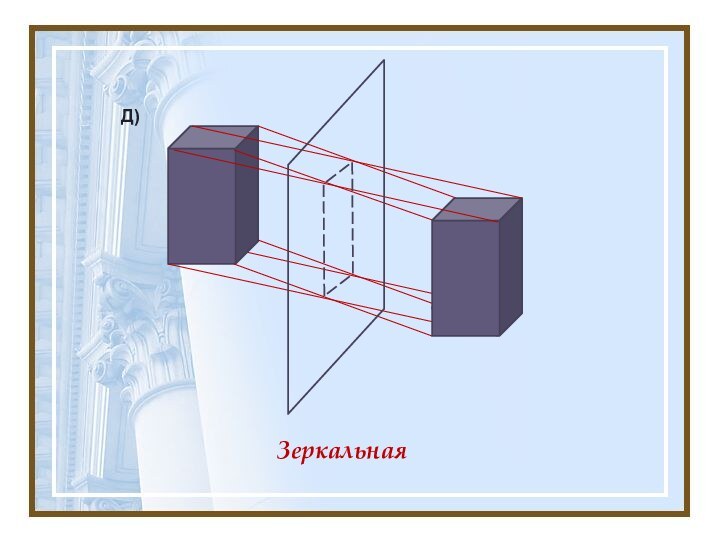
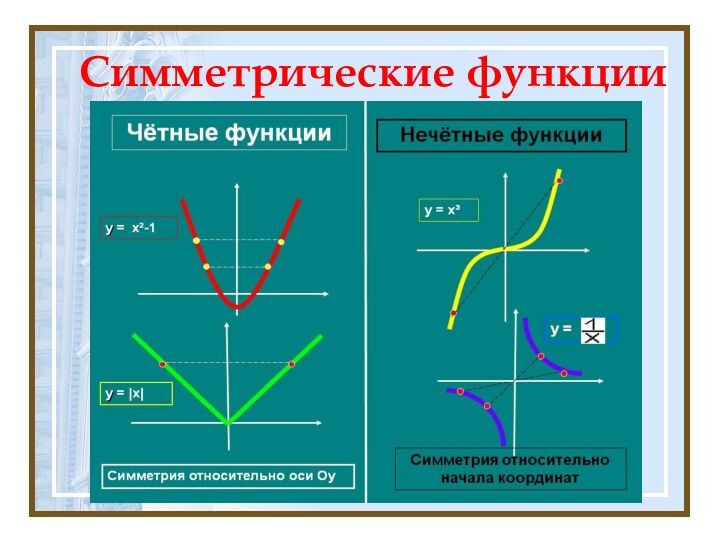
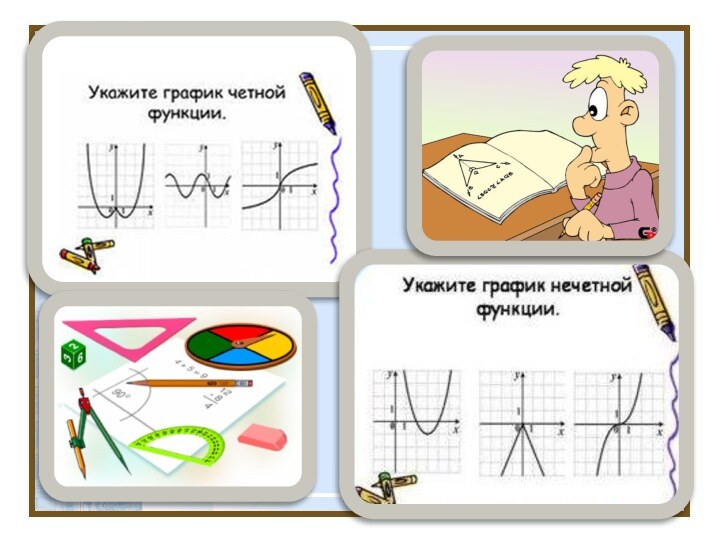
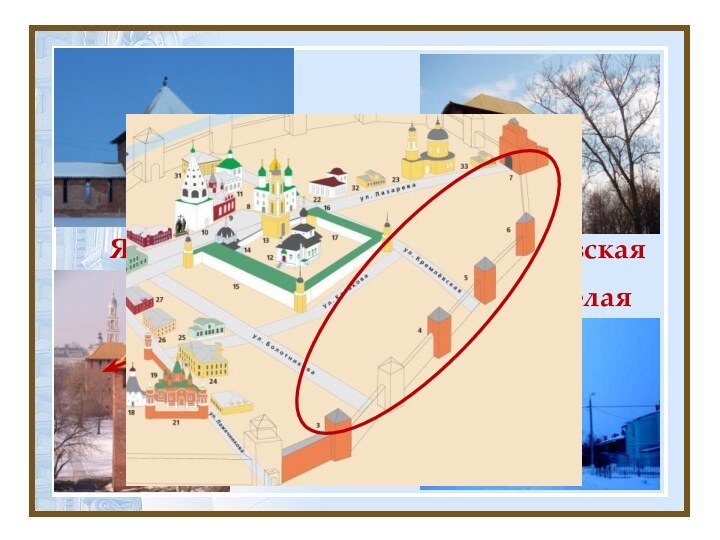
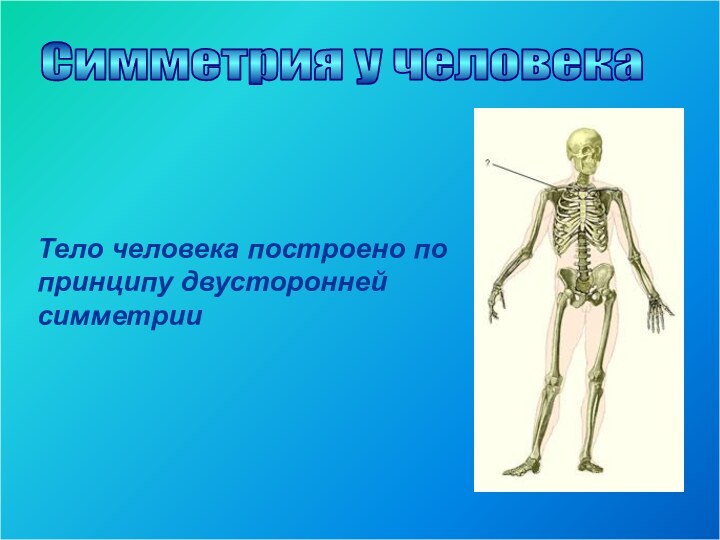
называется нечётной, если справедливо равенствоГрафик нечётной функции симметричен относительно начала координат
Пример 1.
Доказать, что у = х4 — четная функция.
Решение. Имеем: f(х) = х4, f(-х) = (-х)4. Но (-х)4 = х4. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Пример 2.
Доказать, что у = х3~ нечетная функция.
Решение. Имеем: f(х) = х3, f(-х) = (-х)3. Но (-х)3 = -х3. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Слайд 17
Возвратные уравнения 3-й и 4-й степени
Многочлены n-ой степени
f (x) = anxn + an-1xn-1 + … +
a0 называется возвратным, если его коэффициенты, одинаково отдаленные от начала и от конца, равны между собой.Алгебраическое уравнение вида f (x) = 0, где f (x) – возвратный многочлен , называют возвратным уравнением.
Слайд 18
2x3+7x 2 +7x+2 = 0
2x3 +2+7x2
+7x = 0
2 (x3 +1) +7x (x+1) = 0
2
(x+1) (x2 –x+1) + 7x (x+1)=0(x+1) (2x2 - 2x+2+7x)=0
(x+1) (2x2 +5x+2)=0
x+1=0 или 2x 2 +5x +2 =0
x= -1 D= 25 - 16=9
x₁ = -2
x₂ = - 0,5
Ответ:-1;-2;-0,5.
Слайд 19
6х4-35х3+62х2-35х+6х2=0
6х2-35х+62-35/х+6=0
6х2+6/х2-35х-35/х+62=0
6(х2+1/х2)-35(х+1/х)+62=0
Х+1/х=z
(х+1/х)2=z2
Х2+2+1/х2=z2
Х2+1/х2=z2-2
6(z2-2)-35z+62=0
6z2-12-35z+62=0
6z2-35z+50=0
Д=b2-4ac=(-35)2-4*6*50= 1225-1200= 25
Z1=5/2
Z2= 10/3
х+ 1/х=5/2
х+1/х= 10/3
х+ 1/х-5/2 =0
х+1/х-10/3=02х2-5х+2=0 х0 3х2-10х+3=0
Д=25-4*2*2=9 Д= 100-4*3*3=64
Х1= ½ х2 = 2 Х3= 1/3 Х4 = 3
Ответ:1/2;2;1/3;3.
Слайд 20
Системы уравнений второй степени.
Система уравнений второй
степени – это система уравнений, в которой есть хотя
бы одно уравнение второй степени.
Слайд 22
Литература
1. Виленкин Н.Я.Алгебра :издательство «Просвещение» Москва, 1968.
2. Интернет
– ресурсы:
http://ru.wikipedia.org/wiki/
http://festival.1september.ru/
3 Болтянский В.Г. и др. Симметрия в
алгебре. - М.: Наука, 1967.4 Башмаков М.И. Уравнения и неравенства. - М.: Наука, 1971.
5 Березин В.Н. и др. Сборник задач для факультативных
и внеклассных занятий по математике. Книга для учителя. - М.: Просвещение, 1985.
6 Вавилов В.В. и др. Задачи по математике. Алгебра. - М.: Наука, 1987.
7 Черкасов О.Ю. и др. Математика: Справочник для старшеклассников
и поступающих в вузы. - М.: АСТ-Пресс, 2001.
8В.Г.Болтянский, Н.Я.Виленкин Симметрия в алгебре. 2-е издание
9 Винберг Э. Б. Симметрия многочленов. - М.: МЦНМО,
2001. — 24 с: ил. (Серия: «Библиотека „Математическое просвещение"»).
Слайд 23
Проект 2 группы:
Симметрия в архитектуре «Вдоль Кремлевской
стены».
Проект подготовили:
Тихонова В.
Вялых И.
Гурина В.
Швец С.
Короткова В.
Вельчев Н.
Слайд 25 « Чувство симметрии и реальное стремление его выразить
в быту и в жизни существовало в человечестве с
палеолита…Этот опыт многих тысяч поколений ясно
указывает на глубокую эмпирическую основу этого понятия…»
Академик В.И.Вернадский
(1863 – 1945 гг)
Слайд 26 «Изучение археологических памятников показывает, что человечество на заре
своей культуры уже имело представление о симметрии… применение симметрии
в первобытном производстве определялось не столько эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм.»Академик А. В. Шубников
(1887 – 1970 гг)
Слайд 27
Архитектурные стили
готика
барокко
хай-тек
модерн
классицизм
ампир
футуризм
конструктивизм
эклектика
Слайд 32
Литература
1.Большаков М.В. Декор и орнамент в книге:
Альбом. - М.: Книга,
1990.
2. Волошинов
А. В. Математика и искусство. - М.: Просвещение, 2000.3. Гильде В. Зеркальный мир. — М.: Мир, 1982г. 4. Данилова Г.И. Мировая художественная культура. От истоков до
XVII века: учебник для 10 класса общеобразовательных учреждений
гуманитарного профиля, 3 изд. - М.: Дрофа, 2006
5. Пилявский В.И., Тиц А.А., Ушаков Ю.С. История Русской архитектуры. Стройиздат, 1984.
6 Интернет-ресурсы:
История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;
История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;
История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;
http://festival.1september.ru/
http://www.kolomna-kreml.ru/
http://ru.wikipedia.org/wiki/
Слайд 33
Проект 3 группы:
«Симметрия в природе»
Проект подготовили:
Бугаёва Оксана,
Пизикс Алёна,
Кравченко
Катя,
Имерели Данил,
Пизикс Андрей,
Жигалов Саша,
Трапезников Коля,
Боровиков Саша,
Конограев Максим,
Гелеверя Вадик.
Слайд 35 Симметрия является важнейшим свойством природы. Поразительные по красоте
примеры симметрии дают снежинки.
Симметрия в природе
Снежинка обладает поворотной
симметрией.Слайд 36 Под симметрией у животных понимают соответствие в размерах,
форме и очертаниях, а также относительное расположение частей тела,
находящихся на противоположных сторонах разделяющей линии.Симметрия у животных
радиальная (лучистая)
билатеральная
Слайд 37 В XX веке усилиями российских учёных - В
Беклемишева, В Вернадского, В Алпатова, Г.Гаузе - было создано
новое направление в учении о симметрии - биосимметрикаНа примере дерева просматривается симметрия конуса
Симметрия в биологии
Слайд 38 У цветковых растений в большинстве проявляется радиальная и
билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит
из равного числа частей.Симметрия в биологии
Слайд 40
Диссимметрия — это частично расстроенная симметрия,
противоречивое единство симметрии
и асимметрии, обозначающее некоторый упорядоченный отход от симметрии;
это
асимметрия внутри симметрии и наоборот.Слайд 42 Антисимметрия – это сохранение одного свойства объекта и
замена другого свойства на противоположное.
Слайд 45
Литература
Гильде В. Зеркальный мир. — М.: Мир, 1982г
Интернет-ресурсы:
История
Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;
История Русской
архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков;
http://festival.1september.ru/
http://ru.wikipedia.org/wiki/
Слайд 46
Подведение итога
На вопрос «Чему удалось научиться в ходе
