Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Системы счисления

Содержание

Система Счисления (СС) – это способ представления числе и соответствующие ему правила действия над ними.
Системы счисления Система Счисления (СС) – это способ представления числе и соответствующие ему правила действия над ними. Системы счисленияПозиционные Восьмеричная, двоичная, шестнадцатеричная, десятичная и т.д.В позиционной системе счисления значение Недостатки непозиционной системы счисления:Невозможно записывать дробные и отрицательные числаСложно выполнять арифметические операцииДля Основные понятияОснование системы счисления – это количество знаков, которое используется для записи Для записи чисел в позиционной системе с основанием n нужно иметь алфавит и N чисел. Если требуется указать основание системы, к которой относится число, то оно приписывается Развернутой формой записи числа называется запись в виде:Aq=±(an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+a-2q-2+…+a-mq-m)Aq – само числоq- основание Пример №1: получить развернутую форму чисел: 32478₁₀= 3*10000+2*1000+4*100+7*10+8 ==3*10⁴+2*10³+4+10²+7*10¹+8*10º15FC₁₆= 1*1000+5*100+F*10+C101, 11₂ = Пример №2: Перевести числа в десятичную систему счисления:112₃ = 1*3² + 1*3¹
Слайды презентации

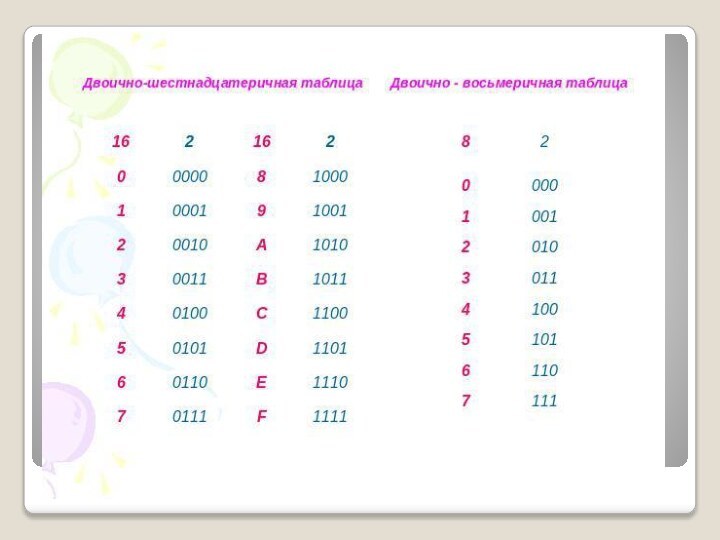
Слайд 2 Система Счисления (СС) – это способ представления числе

Система Счисления (СС) – это способ представления числе и соответствующие ему правила действия над ними.

и соответствующие ему правила действия над ними.

Слайд 3 Системы счисления
Позиционные
Восьмеричная, двоичная, шестнадцатеричная, десятичная и т.д.
В

Системы счисленияПозиционные Восьмеричная, двоичная, шестнадцатеричная, десятичная и т.д.В позиционной системе счисления

позиционной системе счисления значение цифры зависит от её позиции

в числе.

Непозиционные
Римская (I-1, V-5, X-10, L-50, C-100, M-1000, VI-6, IV-4, IX-9)
Унарная (зарубки, палочки) IIII - 4
В непозиционной системе счисления значение цифры не зависит от её позиции в числе.

Слайд 4 Недостатки непозиционной системы счисления:
Невозможно записывать дробные и отрицательные

Недостатки непозиционной системы счисления:Невозможно записывать дробные и отрицательные числаСложно выполнять арифметические

числа
Сложно выполнять арифметические операции
Для записи больших чисел приходится вводить

новые числа

Слайд 5 Основные понятия
Основание системы счисления – это количество знаков,

Основные понятияОснование системы счисления – это количество знаков, которое используется для

которое используется для записи цифр.
Алфавит системы счисления – это

цифры, знаки используемые для записи чисел.
Базис системы счисления – набор степеней основания системы счисления

Слайд 6 Для записи чисел в позиционной системе с основанием

Для записи чисел в позиционной системе с основанием n нужно иметь алфавит и N чисел.

n нужно иметь алфавит и N чисел.

Слайд 7 Если требуется указать основание системы, к которой относится

Если требуется указать основание системы, к которой относится число, то оно

число, то оно приписывается нижним индексом к этому числу.

Слайд 8 Развернутой формой записи числа называется запись в виде:

Aq=±(an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+a-2q-2+…+a-mq-m)

Aq

Развернутой формой записи числа называется запись в виде:Aq=±(an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+a-2q-2+…+a-mq-m)Aq – само числоq-

– само число
q- основание системы счисления
ai - цифры данной

системы счисления
n – число разрядов целой части числа
m – число разрядов дробной части чисел

Слайд 9

Слайд 10 Пример №1: получить развернутую форму чисел:

32478₁₀= 3*10000+2*1000+4*100+7*10+8 =
=3*10⁴+2*10³+4+10²+7*10¹+8*10º
15FC₁₆=

Пример №1: получить развернутую форму чисел: 32478₁₀= 3*10000+2*1000+4*100+7*10+8 ==3*10⁴+2*10³+4+10²+7*10¹+8*10º15FC₁₆= 1*1000+5*100+F*10+C101, 11₂

1*1000+5*100+F*10+C
101, 11₂ = 1*100 + 0*10+ 1*1+ 1*0,1+ 1*0,01

  • Имя файла: sistemy-schisleniya.pptx
  • Количество просмотров: 97
  • Количество скачиваний: 0
- Предыдущая Джаз
Следующая - Теорема Пифагора

Похожие презентации

Конспект урока по математике 1 класс. Пересечение фигур план-конспект урока математики (1 класс) по теме Конспект урока по математике 1 класс. Пересечение фигур план-конспект урока математики (1 класс) по теме 107
Контрольные работы по математике 2 класс материал по математике (2 класс) Контрольные работы по математике 2 класс материал по математике (2 класс) 141
Урок по геометрии по теме: Цилиндр Урок по геометрии по теме: Цилиндр 120
Муравьиные алгоритмы Муравьиные алгоритмы 123
Презентация по математике. презентация к уроку по математике (1 класс) по теме Презентация по математике. презентация к уроку по математике (1 класс) по теме 86
Сложение и вычитание дробей Сложение и вычитание дробей 86
Организация исследовательской работы учащихся Организация исследовательской работы учащихся 96
Правильные многоугольники Правильные многоугольники 99
Математический лабиринт Математический лабиринт 153
Конспект открытого урока по математике 4 класс Решение нестандартных задач план-конспект урока по математике (4 класс) Конспект открытого урока по математике 4 класс Решение нестандартных задач план-конспект урока по математике (4 класс) 62
Презентация Заполним пустые клетки. презентация урока для интерактивной доски по математике (подготовительная группа) Презентация Заполним пустые клетки. презентация урока для интерактивной доски по математике (подготовительная группа) 45
Сложение целых чисел Сложение целых чисел 179
Иррациональные уравнения 11 класс Иррациональные уравнения 11 класс 92
Интегралы.Методы интегрирования Интегралы.Методы интегрирования 135
Скалярное произведение векторов Скалярное произведение векторов 87
Учебно-методический комплект по математике Деление с остатком. Решение задач (конспект, презентация), 3 класс. план-конспект урока по математике (3 класс) по теме Учебно-методический комплект по математике Деление с остатком. Решение задач (конспект, презентация), 3 класс. план-конспект урока по математике (3 класс) по теме 93
Систематизация рациональных приёмов устных вычислений Систематизация рациональных приёмов устных вычислений 100
Ломаная. Выпуклые многоугольники. Правильные многоугольники Ломаная. Выпуклые многоугольники. Правильные многоугольники 89
Презентация по ориентировке на плоскости Шрэк презентация к уроку по математике (средняя группа) Презентация по ориентировке на плоскости Шрэк презентация к уроку по математике (средняя группа) 126
Бордюры Бордюры 198
Математична гра Математична гра 172
Логарифмы Логарифмы 136
Презентация по математике для 5 класса на тему Обыкновенные дроби. Введение понятия. Презентация по математике для 5 класса на тему Обыкновенные дроби. Введение понятия. 101
Процентыи среднее арифметическоев жизни человека Процентыи среднее арифметическоев жизни человека 107
презентация по математике презентация к уроку по математике (1 класс) презентация по математике презентация к уроку по математике (1 класс) 97
Интегрированный урок в 3 классе В царстве грибов методическая разработка по математике (3 класс) по теме 2.  Анализ геометрических фигур Круг. Окружность. Интегрированный урок в 3 классе В царстве грибов методическая разработка по математике (3 класс) по теме 2.  Анализ геометрических фигур Круг. Окружность. 128
129
Презентация к уроку математики в 5 классе по теме Деление десятичной дроби на натуральное число. Повторение действий с десятичными дробями организовано в музыкальной форме и очень понравилось детям. Презентация к уроку математики в 5 классе по теме Деление десятичной дроби на натуральное число. Повторение действий с десятичными дробями организовано в музыкальной форме и очень понравилось детям. 146
N-угольники N-угольники 108
Презентация к уроку математика на темуВасилий Алексеев. Тяжелая атлетика. Действия с десятичными дробями Презентация к уроку математика на темуВасилий Алексеев. Тяжелая атлетика. Действия с десятичными дробями 110