пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой
угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". Рисунок из книги
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
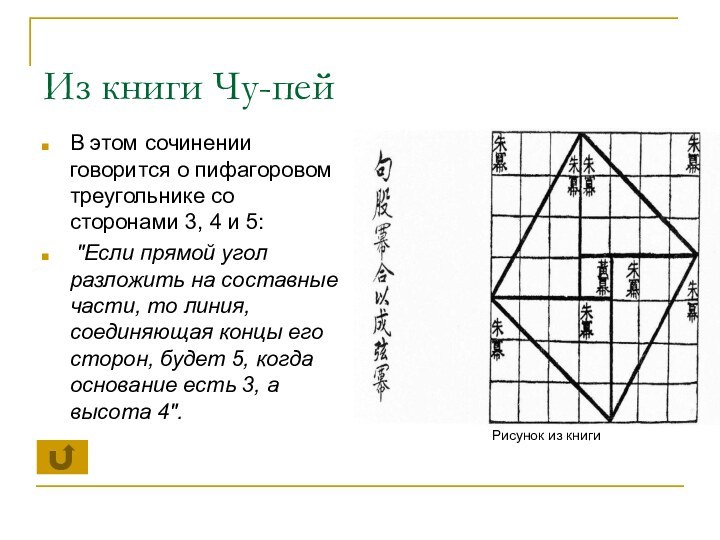





Рисунок из книги