- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Следствия из аксиом стереометрии
Содержание
- 2. Аксиомы стереометрии и некоторые следствия из нихУроки по теме:
- 3. Урок № 1.Тема урока:Стереометрия.Аксиомы стереометрии.
- 4. ПЛАН УРОКА:1.Что такое стереометрия? 2.Аксиомы стереометрии. 3.Решение задач. 4.Итог урока.
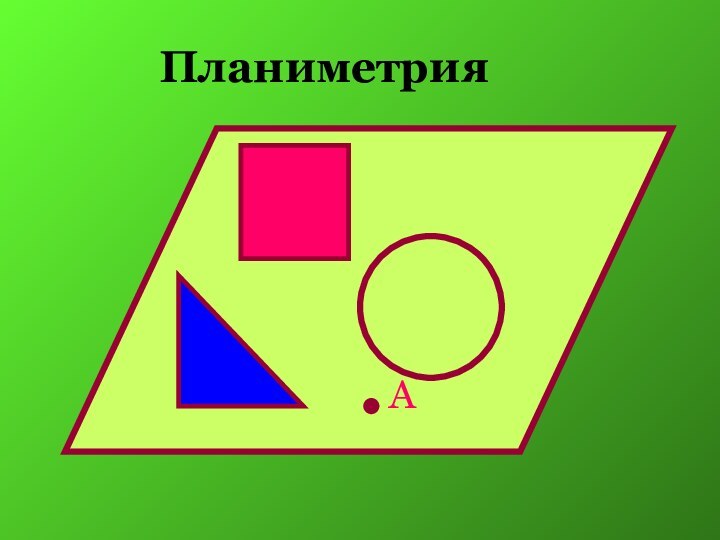
- 5. ПланиметрияА
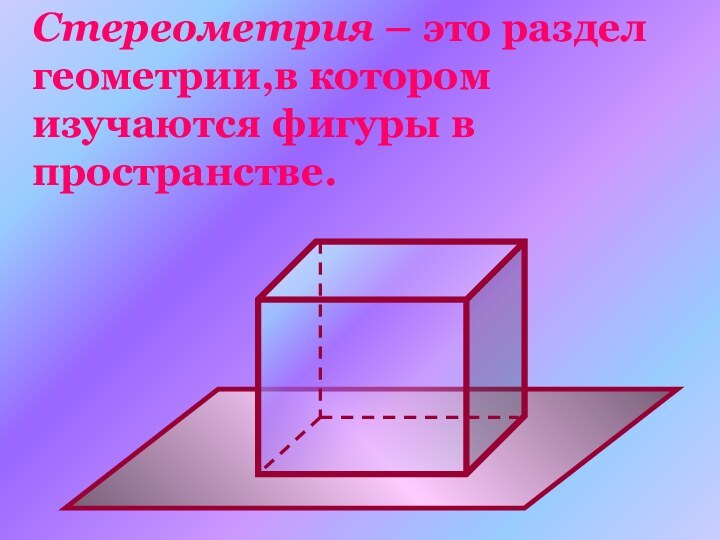
- 6. Стереометрия – это раздел геометрии,в котором изучаются фигуры в пространстве.
- 7. Аксиомы стереометрииКакова бы ни была плоскость,существуют точки,принадлежащие этой плоскости, и точки,не принадлежащие ей. С 1
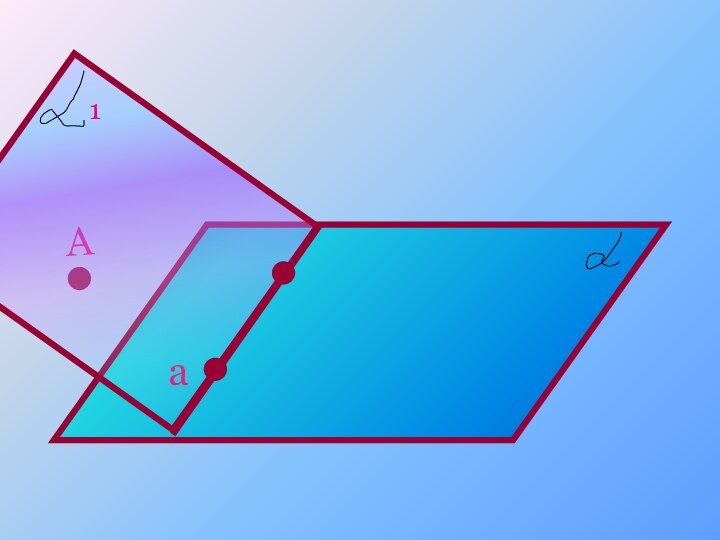
- 8. Если две различные плоскости имеют общую точку,то они пересекаются по прямой,проходящей через эту точку.С 2
- 9. Если две различные прямые имеют общую точку,то
- 10. Аксиомы планиметрии1.Какова бы ни была прямая,существуют точки,принадлежащие
- 11. Задание 1.Постройте изображение куба.АВСДА1В1С1Д1МNКа)назовите плоскости в которых
- 12. Задание 2.Можно ли через точку пересечения двух
- 13. Существование плоскости,проходящей через данную прямую и данную точкуУрок по теме:
- 14. План урока1.Устная работа2.Объяснение нового материала3.Решение задач4.Домашнее задание5.Итог урока
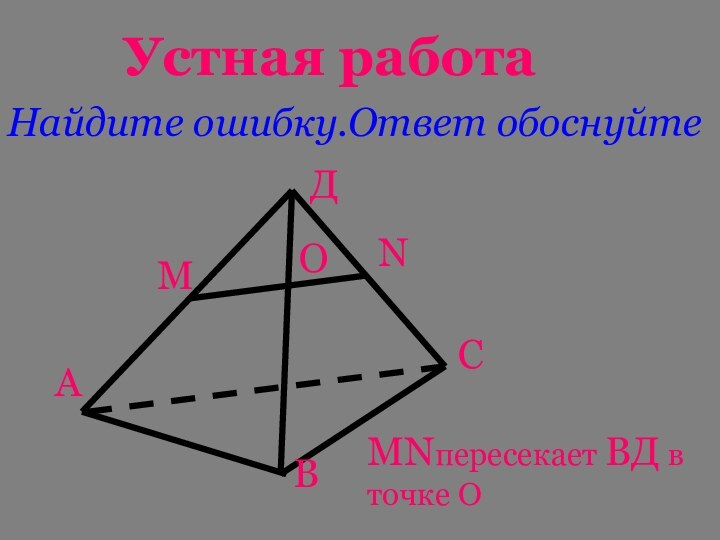
- 15. Устная работаНайдите ошибку.Ответ обоснуйтеАВСДМОNМNпересекает ВД в точке О
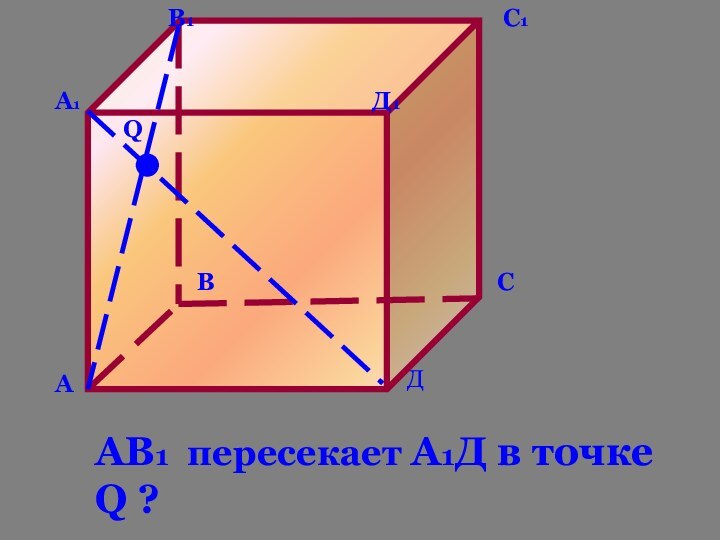
- 16. АВСДА1В1С1Д1QАВ1 пересекает А1Д в точке Q ?
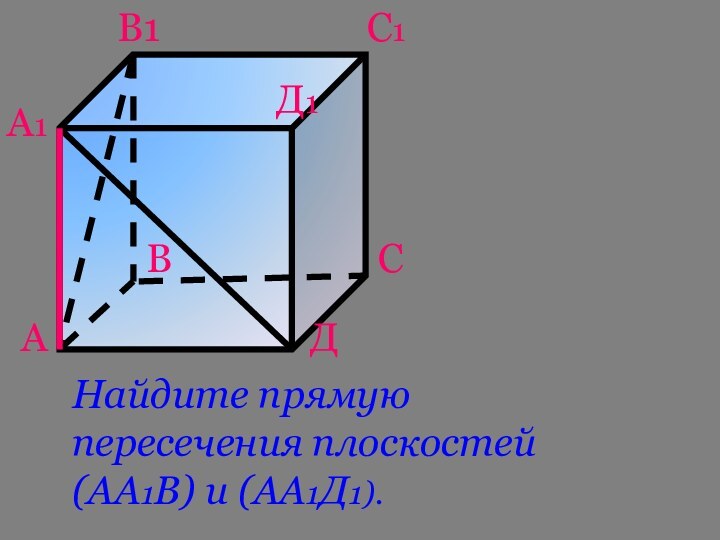
- 17. АВСДА1В1С1Д1Найдите прямую пересечения плоскостей (АА1В) и (АА1Д1).
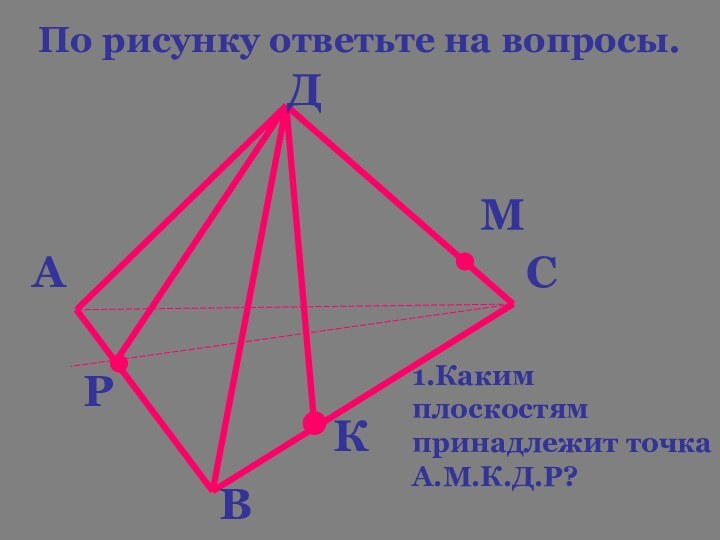
- 18. По рисунку ответьте на вопросы.АДСВРКМ1.Каким плоскостям принадлежит точка А.М.К.Д.Р?
- 19. Теорема 1.1Через прямую и не лежащую на ней точку можно провести плоскость,и притом только одну.
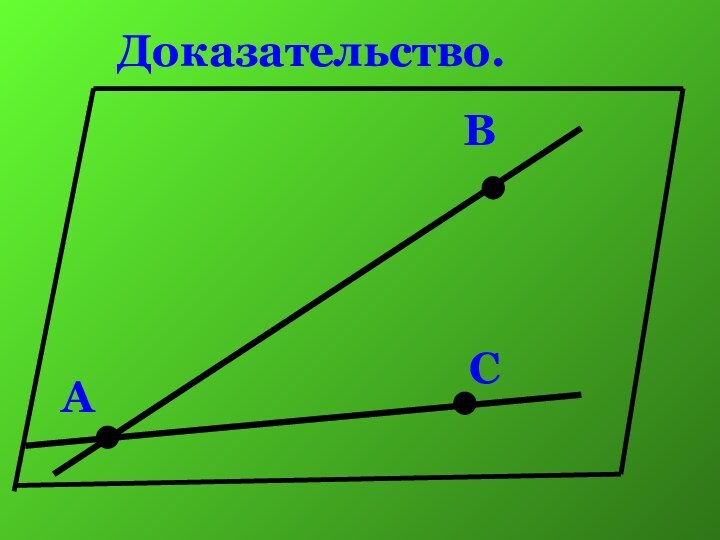
- 20. Доказательство.АВС
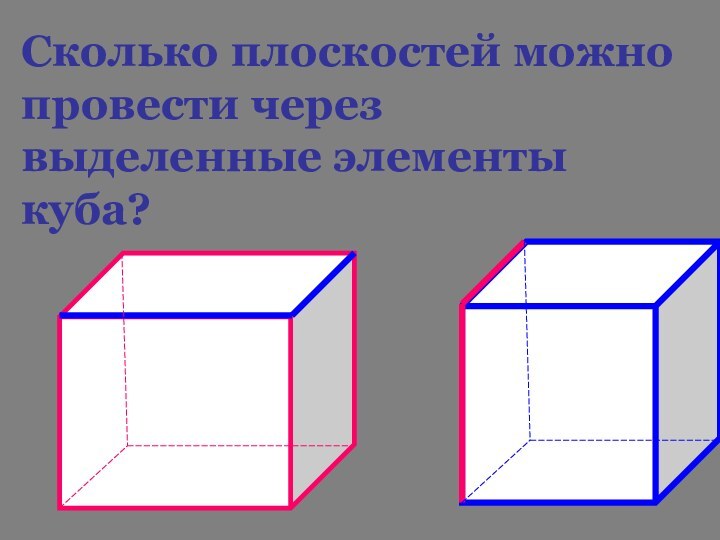
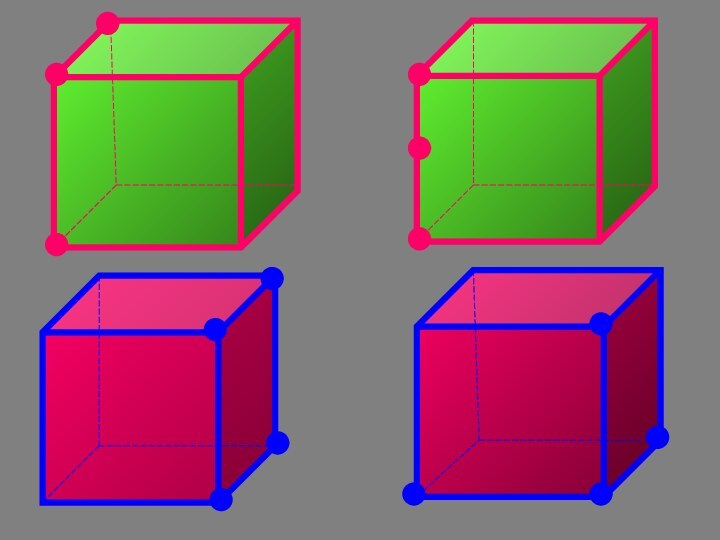
- 21. Сколько плоскостей можно провести через выделенные элементы куба?
- 23. Пересечение прямой с плоскостью(п.3)Теорема 1.2Если две точки прямой принадлежат плоскости,то вся прямая принадлежит этой плоскости.
- 24. аА1
- 25. Из теоремы 1.2 следует:1.Плоскость и прямая имеют
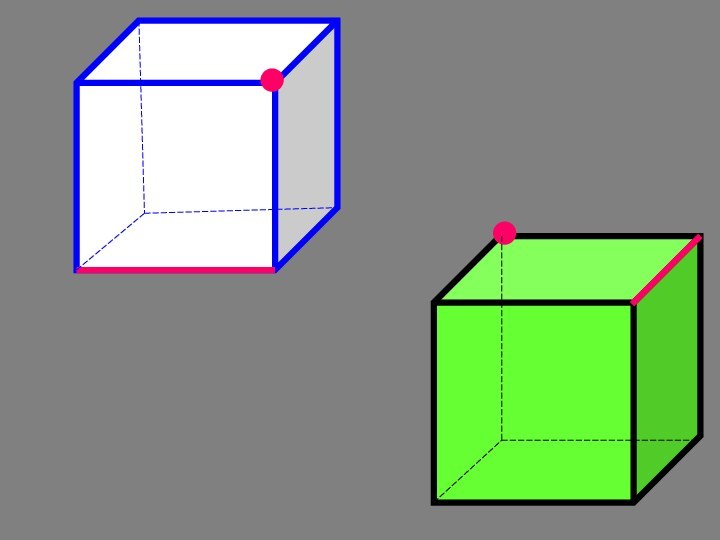
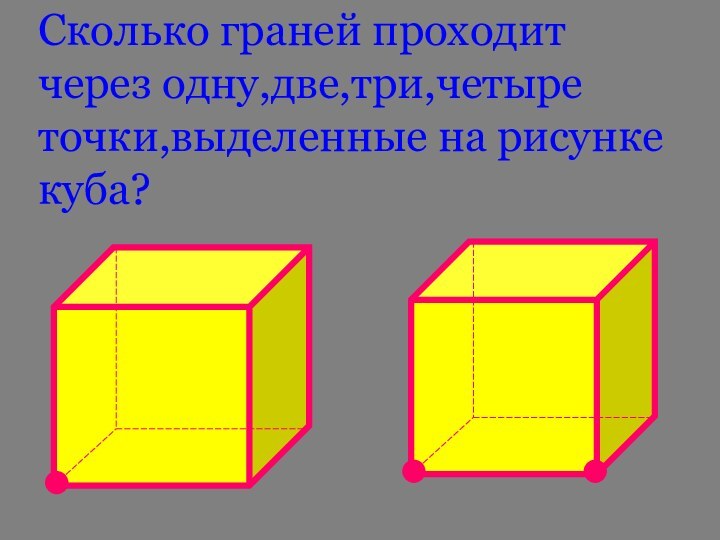
- 26. Сколько граней проходит через одну,две,три,четыре точки,выделенные на рисунке куба?
- 28. Задача.Даны две различные прямые,пересекающиеся в точке А.Докажите,что
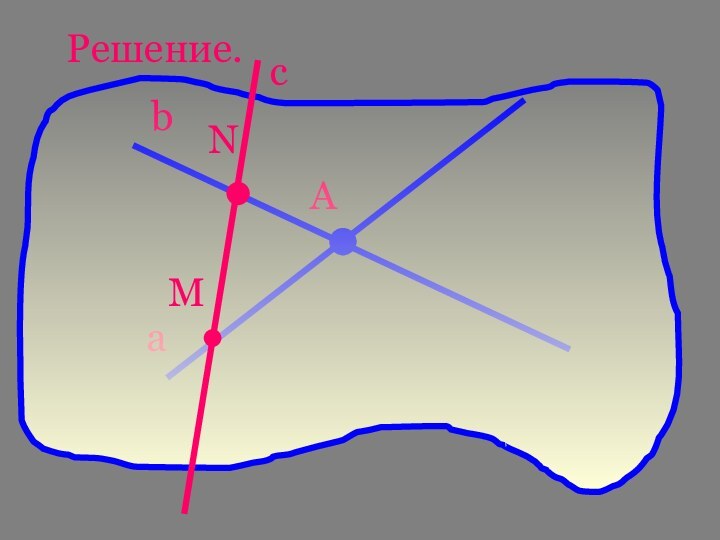
- 29. Решение.аbАсМN
- 30. АВСА1В1С1МКNПо чертежу назовите: а)линию пресечения плоскостей (АВС)
- 31. А1В1С1Д1АВСДВерно ли,что плоскости (ВСД1) и (В1С1Д1)имеют одну
- 32. Постройте:а)точки пересечения прямой ЕF с плоскостями (АВС)
- 33. Урок по теме:Аксиомы стереометрии и их простейшие следствия
- 34. План урока:1.Опрос домашнего задания2.Диктант3.Решение задач4.Самостоятельная работа5.Итог урока6.Домашнее задание
- 35. Устная работа1.Что такое стереометрия?Назовите основные фигуры в
- 36. 5.Отметьте точки А и В,принадлежащие плоскости.Проведите прямую
- 37. Верны ли следующие утверждения?1.Если прямая пересекает две
- 38. 1.Сформулируйте теорему о существовании плоскости,проходящей через данную
- 39. ДиктантТеорема 1.1Существование плоскости,проходящей через данную прямую и
- 40. Самостоятельная работа№1.В пространстве даны три точки А,В,С
- 41. Домашнее задание: п. 1-4 п.5.6 изучить самостоятельно № 5,8.
- 42. Скачать презентацию
- 43. Похожие презентации
Аксиомы стереометрии и некоторые следствия из нихУроки по теме:
























Слайд 7
Аксиомы стереометрии
Какова бы ни была плоскость,существуют точки,принадлежащие этой
плоскости, и точки,не принадлежащие ей. С 1
Слайд 8 Если две различные плоскости имеют общую точку,то они
пересекаются по прямой,проходящей через эту точку.С 2
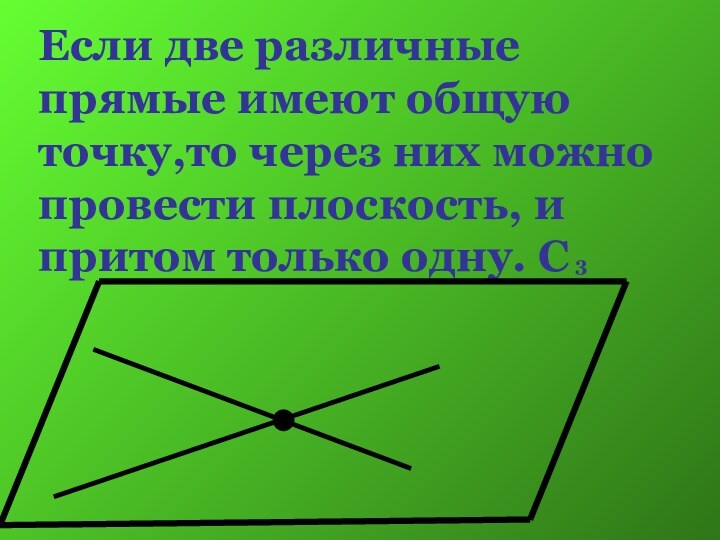
Слайд 9 Если две различные прямые имеют общую точку,то через
них можно провести плоскость, и притом только одну. С
3
Слайд 10
Аксиомы планиметрии
1.Какова бы ни была прямая,существуют точки,принадлежащие этой
прямой,и точки,не принадлежащие ей.Через любые две точки можно провести
прямую,и только одну.2.Из трех точек на прямой одна и только одна лежит между двумя другими.
3.Каждый отрезок имеет определенную длину,большую нуля.Длина отрезка равна сумме длин частей,на которые он разбивается любой его точкой.
4.Прямая,принадлежащая плоскости,разбивает эту плоскость на две полуплоскости.
5.Каждый угол имеет определенную градусную меру,большую нуля.Развернутый угол равен 180.Градусная мера угла равна сумме градусных мер углов,на которые он разбивается любым лучом,проходящим между его сторонами.
6.На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины,и только один.
7.От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой,меньшей 180,и только один.
8.Каков бы ни был треугольник,существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
9.На плоскости через данную точку,не лежащую на данной прямой,можно провести не более одной прямой,параллельной данной.
Слайд 11
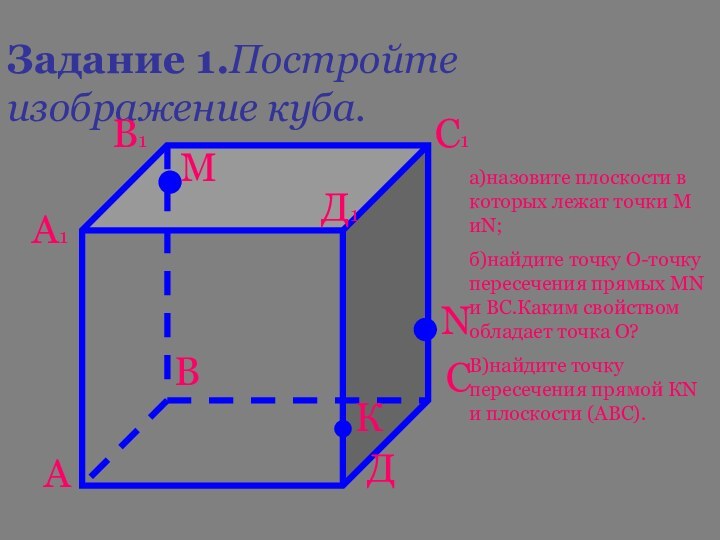
Задание 1.Постройте изображение куба.
А
В
С
Д
А1
В1
С1
Д1
М
N
К
а)назовите плоскости в которых лежат
точки М иN;
б)найдите точку О-точку пересечения прямых МN и
ВС.Каким свойством обладает точка О?В)найдите точку пересечения прямой КN и плоскости (АВС).
Слайд 12 Задание 2.Можно ли через точку пересечения двух данных
прямых провести третью прямую,не лежащую с ними в одной
плоскости?Ответ объясните.а
b
C
Д
Слайд 14
План урока
1.Устная работа
2.Объяснение нового материала
3.Решение задач
4.Домашнее задание
5.Итог урока
Слайд 19
Теорема 1.1
Через прямую и не лежащую на ней
точку можно провести плоскость,и притом только одну.
Слайд 23
Пересечение прямой с плоскостью(п.3)
Теорема 1.2
Если две точки прямой
принадлежат плоскости,то вся прямая принадлежит этой плоскости.
Слайд 25
Из теоремы 1.2 следует:
1.Плоскость и прямая имеют одну
общую точку(прямая пересекает плоскость)
2.Плоскость и прямая имеют две общие
точки(прямая лежит в плоскости)3.Плоскость и прямая не имеют общих точек(прямая и плоскость не пересекаются)
Слайд 28 Задача.Даны две различные прямые,пересекающиеся в точке А.Докажите,что все
прямые,пересекающие обе данные прямые и не проходящие через точку
А,лежат в одной плоскости.
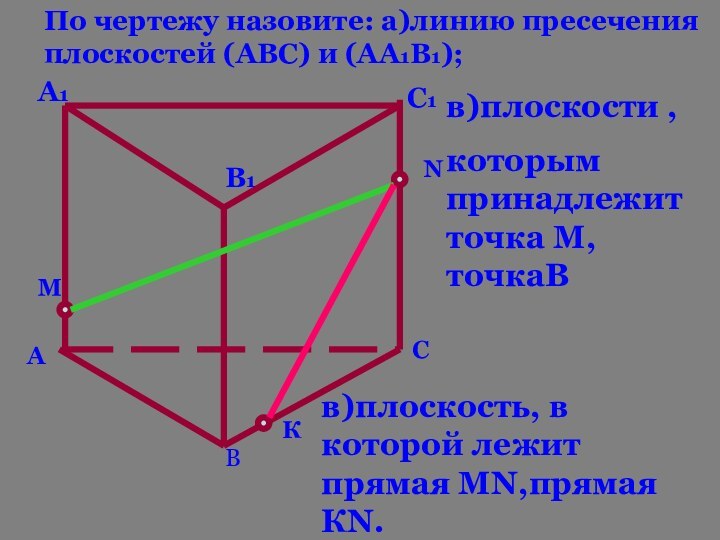
Слайд 30
А
В
С
А1
В1
С1
М
К
N
По чертежу назовите: а)линию пресечения плоскостей (АВС) и
(АА1В1);
в)плоскости ,
которым принадлежит точка М,точкаВ
в)плоскость, в которой лежит прямая
МN,прямая КN.
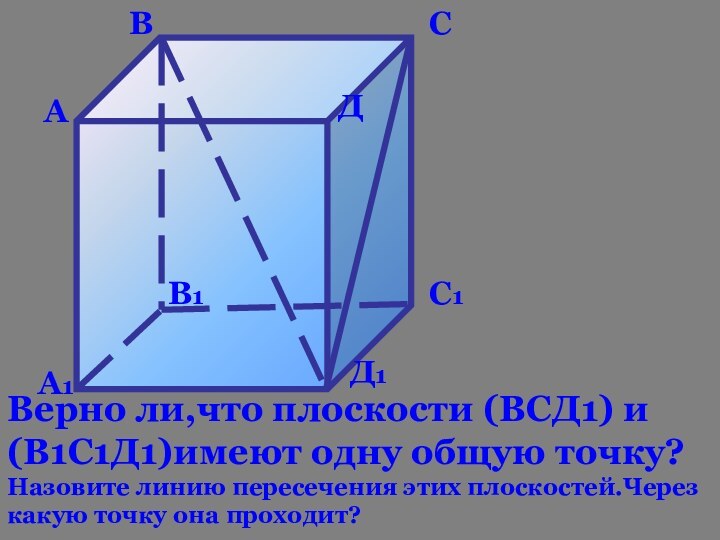
Слайд 31
А1
В1
С1
Д1
А
В
С
Д
Верно ли,что плоскости (ВСД1) и (В1С1Д1)имеют одну общую
точку?
Назовите линию пересечения этих плоскостей.Через какую точку она проходит?
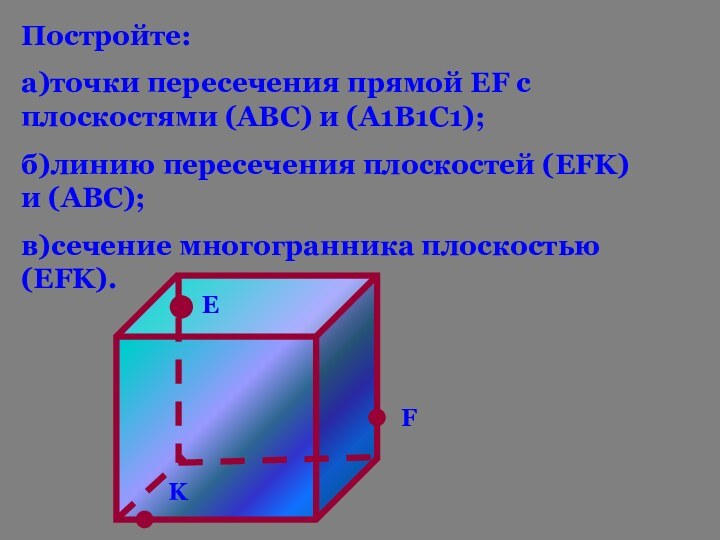
Слайд 32
Постройте:
а)точки пересечения прямой ЕF с плоскостями (АВС) и
(А1В1С1);
б)линию пересечения плоскостей (ЕFK) и (АВС);
в)сечение многогранника плоскостью (ЕFK).
Е
F
K
Слайд 34
План урока:
1.Опрос домашнего задания
2.Диктант
3.Решение задач
4.Самостоятельная работа
5.Итог урока
6.Домашнее задание
Слайд 35
Устная работа
1.Что такое стереометрия?
Назовите основные фигуры в пространстве.
3.Сформулируйте
аксиомы стереометрии С1,С2,С3.
4.Отметьте точку А,не принадлежащую плоскости,и точку В,принадлежащую
плоскости.Как расположена прямая АВ по отношению к плоскости?а)пересекает плоскость;
в)принадлежит плоскости.
Слайд 36 5.Отметьте точки А и В,принадлежащие плоскости.Проведите прямую АВ.Как
расположена прямая АВ по отношению к плоскости?
а)пересекает плоскость;
в)принадлежит плоскости.6.Могут ли прямая и плоскость иметь только одну общую точку? (да,нет)
7.Могут ли прямая и плоскость иметь только две общие точки?(да,нет)
8.Можно ли провести плоскость через четыре произвольные точки пространства?
9.Можно ли через точку пересечения двух прямых провести третью прямую,не лежащую с ними в одной плоскости?
Слайд 37
Верны ли следующие утверждения?
1.Если прямая пересекает две смежные
стороны квадрата,то она лежит в плоскости этого квадрата.
2.Если две
точки окружности лежат в одной плоскости,то и вся окружность лежит в этой плоскости.Слайд 38 1.Сформулируйте теорему о существовании плоскости,проходящей через данную прямую
и данную точку.
Через прямую и не лежащую на ней
точку можно провести плоскость,и притом только одну.2.Сформулируйте теорему о пересечении прямой с плоскостью.
Если две точки прямой принадлежат плоскости,то вся прямая принадлежит этой плоскости.
3.Сформулируйте теорему о существовании плоскости,проходящей через три данные точки.
Через три точки,не лежащие на одной прямой,можно провести плоскость,и притом только одну.
Слайд 39
Диктант
Теорема 1.1
Существование плоскости,проходящей через данную прямую и данную
точку
--------------------------------------------------------------
Теорема 1.2
Пересечение прямой с плоскостью
--------------------------------------------------------------
Теорема 1.3
Существование плоскости,проходящей через три
данные точки
Слайд 40
Самостоятельная работа
№1.В пространстве даны три точки А,В,С такие,что
АВ=14см,ВС=16см,АС=18см.Найдите площадь треугольника АВС.
№2.Четыре точки не лежат в одной
плоскости.Могут ли какие-нибудь три из них лежать на одной прямой? Ответ объясните.№1.В пространстве даны три точкиМ,К,В такие,что МК=13см,МВ=14см,КВ=15см.Найдите площадь треугольника МКВ.
№2.Докажите,что если прямые АВ и СД не лежат в одной плоскости,то и прямые АС и ВД не лежат в одной плоскости.