Слайд 2
Цели темы:
обучающая: знакомство с теорией соединений как самостоятельным
разделом математики, обоснование формулы бинома Ньютона;
развивающая: развитие комбинаторного мышления
и познавательного интереса учащихся;
воспитательная: овладение аппаратом решения вероятностных задач (умственное воспитание).
Слайд 3
Что изучает комбинаторика?
Комбинаторика – раздел математики, в котором
исследуются и решаются задачи выбора элементов из исходного множества
и расположения их в некоторой комбинации, составляемой по заданным правилам.
Слайд 4
Возникновение комбинаторики
Еще математикам Древнего Востока была известна формула
бинома Ньютона с натуральным показателем .
Рождение комбинаторики как
раздела математики связано с трудами Б Паскаля и П.Ферма по теории азартных игр.
Большой вклад в развитие комбинаторных методов был сделан Г.Лейбницем, Я.Бернулли, Л.Эйлером.
В настоящее время комбинаторика используется в кибернетике, дискретной математике, теории планирования и теории информации, архитектуре, дизайне интерьера.
Слайд 5
Самый простой метод решения комбинаторных задач – перебор
всех возможных вариантов
Подсчитать число однобуквенных слов русского языка.
Ответ:11
Перечислить виды: 1)треугольников, 2)четырехугольников.
Ответ:1)равносторонний, равнобедренный, разносторонний; остроугольный, прямоугольный, тупоугольный.
2) параллелограмм, прямоугольник, ромб, квадрат, трапеция.
В магазине продают бейсболки трех цветов: синие, красные и черные. Ваня и Андрей покупают себе по одной. Сколько существует различных вариантов покупки?
Ответ:9 вариантов.
Слайд 6
Полный перебор может осуществляться с помощью деревьев
С помощью
цифр 3 и 5 записать все возможные трёхзначные числа
(цифры могут повторяться).
Ответ: 8 чисел.
Слайд 7
Полный перебор может осуществляться с помощью таблиц и
графов
Встретились пятеро, каждый пожал другому руку. Сколько было рукопожатий?
Ответ:10.
С
помощью таблицы вариантов
перечислить все возможные
двухбуквенные коды, в которых
используются буквы: x,y,z.
Ответ: 9.
Слайд 8
Правило произведения
При большом количестве имеющихся элементов полный перебор
затруднителен. Правило произведения позволяет упростить подсчет числа определенных соединений.
Сформулируем это правило. Если существует вариантов выбора первого элемента и для каждого из них имеется вариантов выбора второго элемента, то существует различных пар с выбранными первым и вторым элементами.
Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр 0,2,4,6,8?
Ответ: 4∙5 = 20.
Слайд 9
Обобщение правила произведения
Задача 2. В кафе имеются 3
первых блюда, 5 вторых и 2 третьих. Сколькими способами
посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Ответ:3∙5∙2 = 30.
Задача 3. Пётр решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор различные по цвету и фасону предметы: 5 пар брюк, 6 камзолов, 3 шляпы, 2 пары сапог. Сколько различных карнавальных костюмов он может составить из этих предметов?
Ответ: 5∙6∙3∙2 = 180.
Слайд 10
Основные задачи комбинаторики
Основными задачами комбинаторики считаются следующие:
составление упорядоченных множеств (образование перестановок);
составление
подмножеств данного множества (образование сочетаний)
составление упорядоченных подмножеств данного множества (образование размещений).
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма.
Ответ: а)да; б)нет; в)нет; г)да.
Слайд 11
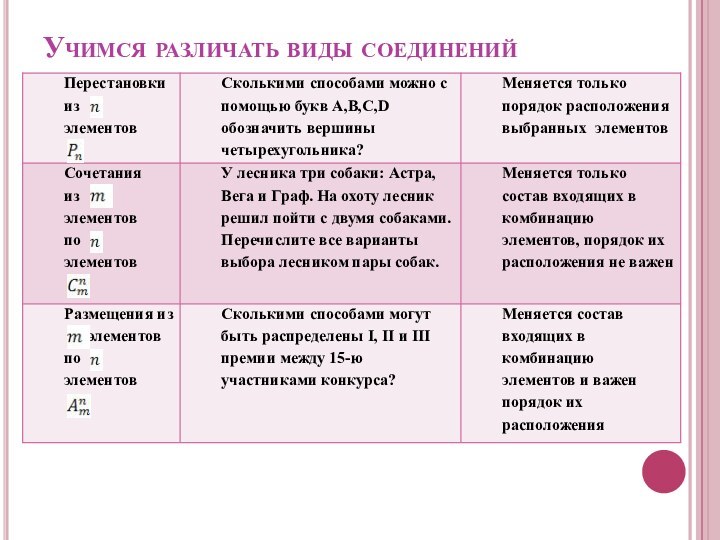
Учимся различать виды соединений
Слайд 12
Перестановки
Перестановками из элементов называются соединения, которые
состоят из элементов и отличаются одно от
другого только порядком их расположения.
Permutation (фр.) – перестановка.
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?
Ответ:6.
Слайд 13
Размещения
Размещениями из элементов по
элементов
( ≤
) называются такие соединения, каждое из которых содержит элементов, взятых из
данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Задача 1. Сколькими способами можно изготовить трёхцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
Ответ: 210.
Слайд 14
Размещения
Задача 2. Сколькими
способами могут занять
I, II, III
места 8 участниц
финального забега на
дистанции 100 м?
Ответ:
366.
Задача 3. Из 30 участ-
ников собрания надо
выбрать председателя и секретаря. Сколькими
способами это можно сделать?
Ответ: 870.
Слайд 15
Сочетания
Сочетаниями из элементов по
элементов
( ≤ )
называются такие соединения, каждое из которых содержит элементов, взятых из
данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Задача 1. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Ответ: 21.
Слайд 16
Сочетания
Задача 2. Сколькими
способами можно соста-
вить букет из трёх
цвет-
ков, выбирая цветы из
девяти имеющихся?
Ответ: 84.
Задача 3.
В классе
учатся 16 мальчиков и 12 девочек. Сколькими способами можно выделить 4 мальчиков и 3 девочек для уборки территории?
Ответ:
Слайд 17
Бином Ньютона
Бином Ньютона – это
выражение
вида
Треугольником Паскаля
пользуются при возведении
бинома
в натуральные
степени.
Примеры.
Слайд 18
Проверь себя
1. Сколькими способами 4 вора могут разбежаться
на 4 разные стороны?
2. Из колоды в 36 карт выбирают 5 карт и одновременно открывают их. Найдите число всех возможных вариантов выбранных карт.
3. Сколькими способами из класса, где учатся 24 ученика, можно выбрать: а)двух дежурных; б)старосту и помощника старосты?
Ответ: а)276; б)552.
4. «Проказница Мартышка, Осёл, Козёл да косолапый Мишка задумали сыграть квартет». Сколькими способами они могут выбрать каждый для себя по одному инструменту из 10 данных различных инструментов?
Ответ:
Слайд 19
О пользе комбинаторики или лишних знаний не бывает
Слайд 20
О пользе комбинаторики или лишних знаний не бывает
Слайд 21
О пользе комбинаторики или лишних знаний не бывает