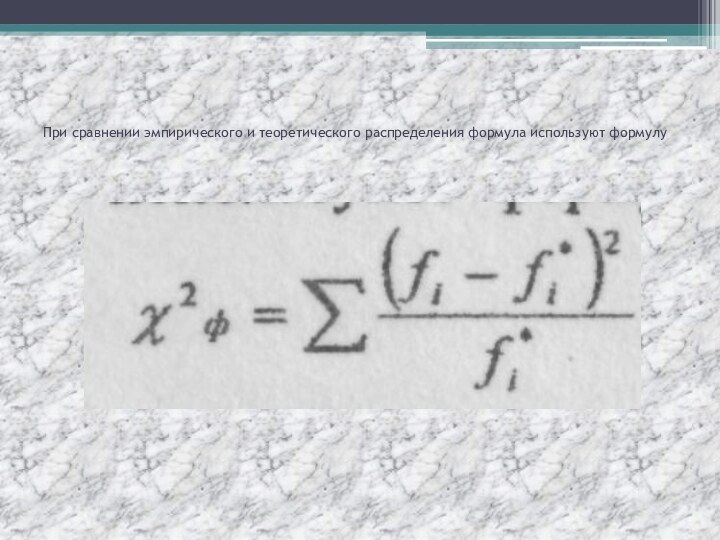Слайд 2
План лекции:
1. Критерии проверки статистических гипотез
2. Параметрические критерии:
Критерий Стьюдента, Критерий Фишера
3. Непараметрические критерии: Хи-квадрат, критерий Колмогорова-Смирнова,
Критерий знаков, Критерий Мана-Уитни, критерий Уилка-Шапиро и др.
4. Применение статистических критериев в анализе почвенных данных
Слайд 3
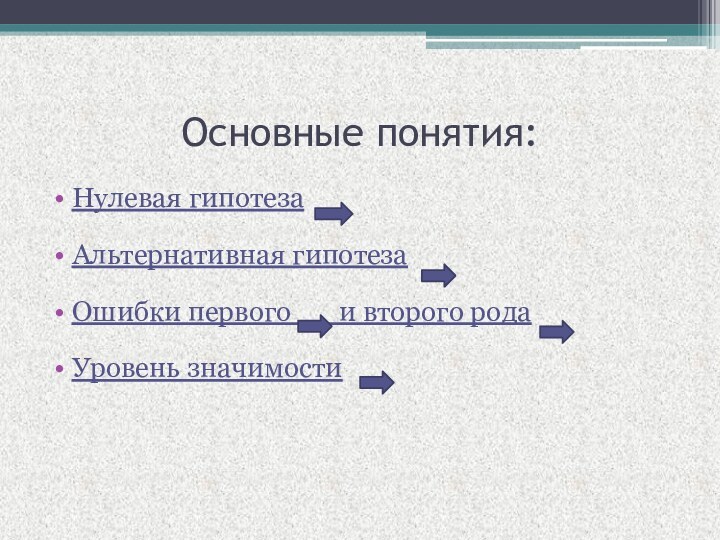
Основные понятия:
Нулевая гипотеза
Альтернативная гипотеза
Ошибки первого
и второго рода
Уровень значимости
Слайд 4
Этапы проверки статистических гипотез
Формулировка основной гипотезы H0 и

конкурирующей гипотезы H1. Гипотезы должны быть чётко формализованы в
математических терминах.
Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.
Расчёт статистики φ критерия такой, что:
её величина зависит от исходной выборки ;
по её значению можно делать выводы об истинности гипотезы H0;
сама статистика φ должна подчиняться какому-то известному закону распределения, т.к. сама φ является случайной в силу случайности .
Построение критической области. Из области значений φ выделяется подмножество таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство . Это множество и называется критической областью.
Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.
Слайд 5
Статистическая гипотеза - некоторое предположение о свойствах генеральной
совокупности, которой принадлежит выборка.
Слайд 6
Нулевая гипотеза (Н0) - предположение о том, что
между генеральными параметрами сравниваемых групп разница равна нулю, или
различия между выборочными показателями носят случайный характер
Слайд 7
Если выборка из совокупности 1 имеет параметры µ1
и σ1, а выборка из совокупности 2 соответственно µ2σ2,
то:
µ1=µ2, σ1=σ2
и
µ1-µ2=0, σ1-σ2 =0
Слайд 8
Нулевая гипотеза может иметь в виду µ=α, где
α- какое-то число.
Слайд 9
Альтернативная (противоположная) гипотеза – противопоставляется нулевой гипотезе и
исходит из того, что:
µ1-µ2≠0
и
σ1-σ2≠0
Слайд 10
Критерии проверки гипотез:
Число степеней свободы (k) – числа,
показывающие количество свободно варьирующих элементов или членов статистической совокупности,
способных принимать любые произвольные значения.
Уровень значимости (α) – значение вероятности, при котором различия, наблюдаемые между выборочными показателями, можно считать несущественными, случайными.
Слайд 11
Критерии значимости
Параметрические
Критерий Стьюдента
(t)
Критерий Фишера
(F)
Непараметрические
Критерий
Хи-квадрат
(χ²)
Критерий
Колмогорова-Смирнова (d)
Критерий знаков
(z)
Критерий
Мана-Уитни (U)
Критерий
Уилка-Шапиро (W)
Т-критерий Уилксона (T)
Слайд 12
Параметрические критерии
строятся на основе параметров выборочной совокупности
Непараметрические
критерии
функции от вариант данной совокупности с их частотами
Слайд 13
Область значений случайной величины
Область допустимых значений
Область маловероятных значений
Слайд 14
Критическое значение – соответствует границе между областью допустимых
и областью маловероятных значений.
Устанавливается в зависимости от принятого
уровня значимости (α). Критерии проверки гипотез
Слайд 15
Выделяют три вида критических областей:
Двусторонняя критическая область определяется
двумя интервалами, где находят из условий .
Левосторонняя критическая
область определяется интервалом , где xα находят из условия P(φ < xα) = α.
Правосторонняя критическая область определяется интервалом , где xα находят из условия P(φ > xα) = α.
Слайд 16
Ошибка первого рода
Уровень значимости характеризует ту вероятность, которой
решено пренебрегать в данном исследовании.
Отклонение нулевой гипотезы при
попадании значения случайной величины в критическую область нельзя рассматривать как доказательство того, что гипотеза неверна, так как значения, выходящие за пределы области принятия гипотезы Но могут иметь место и в случае правильности нуль-гипотезы, и вероятность такого события известна - она равна α.
Отклоняя правильную нулевую гипотезу, мы допускаем так называемую ошибку первого рода, принятый же уровень значимости α характеризует риск допустить такую ошибку.
Слайд 17
Ошибка второго рода
Принятие нулевой гипотезы, когда она неверна,
носит название ошибки второго рода. Вероятность такой ошибки обозначается
( β ).
С вероятностью 1 - β принятия нулевой гипотезы, когда она верна, связывается в математической статистике понятие мощность критерия.
Слайд 18
Уменьшая вероятность ошибки первого рода (α), мы неизбежно
увеличиваем вероятность ошибки второго рода (β).
Выбор уровня значимости
α (устанавливается обычно α, а не β) определяется условиями проведения эксперимента, ответственностью выводов и учетом того, ошибка какого рода наиболее нежелательна.
В большинстве случаев принимают α = 0,05 (5%), что соответствует доверительной вероятности Р = 0,95.
Слайд 20
Распределение Стьюдента (или t-распределение) - это распределение отклонений
нормально распределенной случайной величины от генерального среднего, нормированных выборочной
оценкой среднего квадратического отклонения.
Это распределение зависит от числа степеней свободы γ, с которым найдена оценка среднего квадратического отклонения.
Слайд 21
Классическим примером распределения Стьюдента является распределение стандартизованных отклонений
где:
х - нормально распределенное выборочное среднее;
µ- генеральное среднее; Sх
- ошибка среднего, вычисленная по выборке объема n,
t - значение случайной величины, распределенной по Стьюденту с ν= n - 1 числом степеней свободы.
Слайд 22
Кривая распределения Стьюдента похожа по
внешнему виду на
кривую нормального распределения: она одновершинна, симметрична, ее ветви асимптотически
приближаются к оси абсцисс.
При ν ->∞ распределение Стьюдента стремится к нормальному распределению с параметрами µ = 0 и σ = 1.
Слайд 23
Кривые нормального распределения
(Z -сплошная линия) и распределения
t-Cтьюдента при ν=3 (пунктирная линия)
Слайд 24
Наибольшее отличие распределения Стьюдента от нормального наблюдается при
ν=1, когда при значениях переменной величины t, близких к
среднему, плотность вероятности распределения Стьюдента меньше, а при значениях, сильно отличающихся от среднего, больше, чем при нормальном распределении.
Слайд 26
t – распределение – частный случай нормального распределения;
t – распределение – симметрично;
t – распределение отражает специфику
распределения малой выборки по нормальному закону.
Слайд 28
Сравнение средних арифметических корреляционно не связанных между собой
выборок, взятых из нормально распределяющихся совокупностей с их параметрами
µ1σ1² µ2σ2² исходят из предположения , что разница между ними возникла случайно (d=x1-X2). В качестве критерия проверки гипотезы служит переменная величина:
Слайд 29
Нулевая гипотеза опровергается (Н0), если tф≥tst для принятого
уровня значимости и числа степеней свободы k=n1+n2-2.
Слайд 30
Распределение F Фишера.
Распределение представляющее собой случайную величину,
распределение которой было изучено Фишером, названо его именем и
обозначено буквой F.
Слайд 31
Если имеются две оценки S1² и S2² одной
и той же дисперсии σ² нормально распределенной случайной величины,
то, принимая, что S1²>S2², можно найти отношение этих оценок. При этом всегда берется отношение большей дисперсии к меньшей:
Слайд 32
С увеличением v1 и ν2 обе оценки стремятся
к одному и тому же параметру σ², F при
этом стремится к единице.
Чем меньше ν1 и ν2, тем больше шансов получить в случайном порядке достаточно отличные от единицы значения F.
Слайд 33
Распределение F зависит от числа степеней свободы ν1
и ν2, с которыми найдены оценки дисперсий в числителе
(ν1) и в знаменателе (ν2).
Слайд 35
Если выборки взяты из разных совокупностей с неравными
параметрами σ1² и σ2², то Fф≥Fst и нулевая гипотеза
должна быть опровергнута (Н0).
Слайд 37
Распределение Хи-квадрат (χ2(n))
Допустим, что случайная величина Z распределена
нормально с параметрами . Если взять n случайных значений
z и найти сумму их квадратов, то полученная сумма будет представлять собой значение некоторой случайной величины, обозначаемой χ2 (хи-квадрат):
Слайд 38
Основные свойства критерия:
Случайная величина χ2, будучи суммой квадратов,
всегда положительна и должна зависеть от числа слагаемых.
Величина
χ2 может принимать значения от 0 до ∞.
Слайд 39
Вид кривой распределения существенно зависит от числа слагаемых,
точнее, от числа независимых слагаемых, т.е. от числа степеней
свободы ν. При очень малых ν распределение сильно асимметрично, но асимметрия быстро уменьшается по мере увеличения числа степеней свободы. Для распределения χ2 среднее число равно числу степеней свободы, а дисперсия - удвоенному числу степеней свободы:
Слайд 40
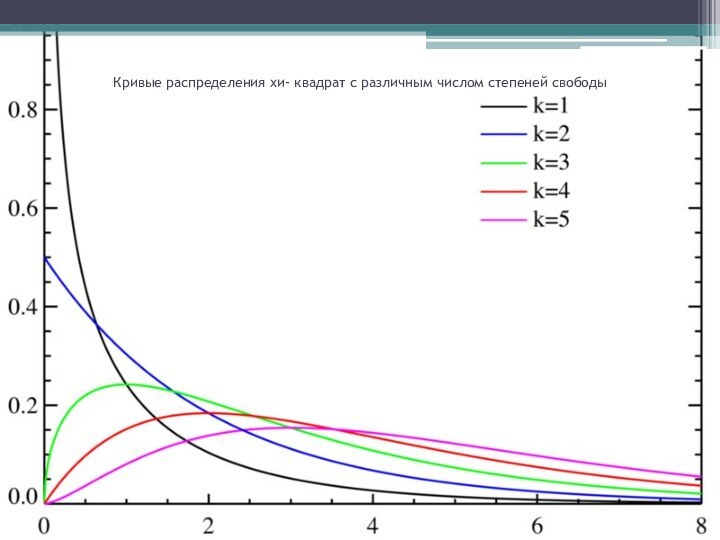
Кривые распределения хи- квадрат с различным числом степеней
свободы
Слайд 41
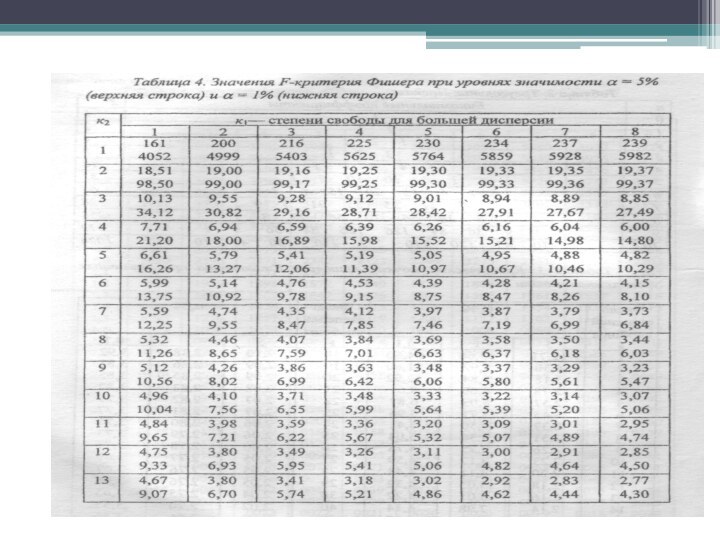
Так как закон распределения известен, то не составляет
большого труда вычислить критические значения χα2, случайно превысить которые
при заданном ν можно с вероятностью α.
Слайд 42
Для выборок равного объема, n1=n2 и N= n1+n2
Слайд 43
Для выборок разного объема, n1≠n2
Слайд 44
При сравнении эмпирического и теоретического распределения формула используют
формулу
Слайд 46
U-критерий Манна-Уитни (англ. Mann-Whitney U test) — непараметрический
статистический критерий, используемый для оценки различий между двумя выборками
по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками. Другие названия: критерий Манна-Уитни-Уилкоксона (англ. Mann-Whitney-Wilcoxon, MWW), критерий суммы рангов Уилкоксона (англ. Wilcoxon rank-sum test) или критерий Уилкоксона-Манна-Уитни (англ. Wilcoxon-Mann-Whitney test).
Слайд 47
Простой непараметрический критерий. Метод определяет, достаточно ли мала
зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений
параметра в первой выборке и таким же во второй выборке).
Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
Слайд 48
Для применения U-критерия Манна-Уитни нужно произвести следующие операции:
1.
Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив
их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным: N = n1 + n2, где n1 — количество единиц в первой выборке, а n2 — количество единиц во второй выборке.
Слайд 49
2. Разделить единый ранжированный ряд на два, состоящие
соответственно из единиц первой и второй выборок. Подсчитать отдельно
сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм (Tx), соответствующую выборке с nx единиц.
Слайд 50
3. Определить значение U-критерия Манна-Уитни по формуле:
Слайд 51
4. По таблице для избранного уровня статистической значимости
определить критическое значение критерия для данных n1 и n2.
Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.
Слайд 52
5. При справедливости нулевой гипотезы критерий имеет матожидание
и дисперсию и при достаточно большом объёме выборочных данных
(n1>19, n2>19) распределён практически нормально.
Слайд 54
Ограничения применимости критерия
1. В каждой из выборок должно
быть не менее 3 значений признака. Допускается, чтобы в
одной выборке было два значения, но во второй тогда не менее пяти.
2. В выборочных данных не должно быть совпадающих значений (все числа - разные) или таких совпадений должно быть очень мало.
Слайд 55
Критерий Колмогорова -Смирнова
В статистике критерий согласия Колмогорова (также
известный, как критерий согласия Колмогорова-Смирнова) используется для того, чтобы
определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.
Критерий Колмогорова-Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных и наиболее широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках.
Слайд 56
Критерий Колмогорова-Смирнова о проверке гипотезы об однородности двух
эмпирических законов распределения является одним из основных и наиболее
широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках.
Слайд 57
Максимальная по модулю разность между соответствующими накопленными относительными
частотами является фактическим значением критерия Колмогорова-Смирнова.
Слайд 58
Теоретическое значение критерия Колмогорова Смирнова вычисляется по формуле: