Слайд 2
Цель урока:
Закрепить и проверить знания учащихся по теме
«Свойства углов, образованных при пересечении двух параллельных прямых третьей»
и «Признаки параллельных прямых».
Вывести доказательство свойства углов треугольника.
Научить применению этих свойств при решении простейших задач.
Способствовать развитию познавательной активности учащихся с помощью исторического материала.
Воспитывать навыки аккуратности при построении чертежей.
Слайд 4
Ход урока
Повторение и проверка знаний по теме «Параллельные
прямые»
Устный счет
Из истории математики
Закрепление изученного материала
Итог урока
Домашнее задание
Слайд 5
Самостоятельная работа
Вариант 1
Определите, какие стороны у четырехугольника параллельны.
Ответ обоснуйте.
Найти все углы ABC, если
m II AC
Вариант 2
Определите, какие стороны у четырехугольника параллельны. Ответ обоснуйте.
Найти углы 3 и 4 MNK, если
NC II MK
Слайд 6
Устный счет
Проверим устно решение второй задачи.
Сформулируйте определение, признаки
параллельности прямых и свойств углов (внутренних накрестлежащих и внутренних
односторонних углов) при параллельных прямых и секущей.
Слайд 7
Из истории математики
Евклид (3 век до нашей эры)
В труде «Начала» приводит
такое определение:
«Параллельные суть прямые,
которые находятся в одной
плоскости, и будучи
продолжены в обе стороны
неограниченно, ни стой,
ни с другой стороны между
собой не встречаются.»
Слайд 8
Из истории математики
Посидоний (1 век до нашей эры)
«Две прямые
лежащие в одной плоскости равностоящие друг от друга»
Слайд 9
Из истории математики
Папп
(вторая половина 3 век до
нашей эры)
древнегреческий ученый ввел символ параллельности прямых
– знак
Слайд 10
Из истории математики
Риккардо (1720 - 1823)
Впоследствии английский экономист Риккардо
этот символ использовал как знак
равенства.
Слайд 11
Из истории математики
Только в XVIII веке стали использовать
символ параллельности прямых – знак
Слайд 12
Из истории математики
Ни на миг не прерывается
живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный
предками. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали предположения – гипотезы, пытались обосновать и доказать.
Слайд 13
Из истории математики
В это время и сложилось
утверждение:
«В споре рождается истина.»
Слайд 14
Практическая работа
Вариант 1
Опытным путем
определите, чему равна сумма углов треугольника (использовать транспортир, модели
остроугольного, тупоугольного и прямоугольного треугольников).
Вариант 2
Какой угол получится, если его составить из углов треугольника. Чему равна его градусная мера. Использовать три модели треугольников. Углы треугольника можно «отрывать»
Слайд 15
ГИПОТЕЗЫ
Сумма углов треугольника равна 180º.
Углы треугольника образуют развернутый
угол.
Слайд 16
ВОПРОСЫ К КЛАССУ
Можно ли быть уверенным
в том, что в каждом треугольнике сумма углов равна
180º?
Можно ли измерить углы
любого треугольника?
Слайд 17
Теорема о сумме углов треугольника
Слайд 18
КОНСПЕКТ
Теорема. Сумма углов треугольника равна 180º.
Дано: Δ АВС.
Доказать
ے1 +ے2 +ے3=180º
Доказательство:
Рекомендации: выполнить дополнительные построения:
Способ 1 – m II AC, где B II m
Способ 2 – луч BD II AC
Слайд 19
Из истории математики
Первое доказательство было сделано
еще Пифагором ( 5 век до нашей эры) В
первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника.
Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.
Слайд 20
ЗАКРЕПЛЕНИЕ
Устная работа по готовым чертежам.
Слайд 21
ЗАКРЕПЛЕНИЕ
Письменная работа
по учебнику.
Стр.53
№19 (2),
№22 (1),
№23 (2),
Слайд 22
№19 (2)
Пусть коэффициент пропорциональности равен k , то
ے1=2k град ,
ے 2=3k град , ے
3=4 k град.
Сумма углов треугольника равна 180º, то
2k + 3k + 4 k = 180, 9 k = 180, k = 20.
Таким образом, ے1= 2 ∙ 20 º =40 º,
ے 2=3 ∙ 20 º =60 º, ے 3= 4 ∙ 20 º =80 º .
Ответ: 40 º, 60 º, 80 º .
Слайд 23
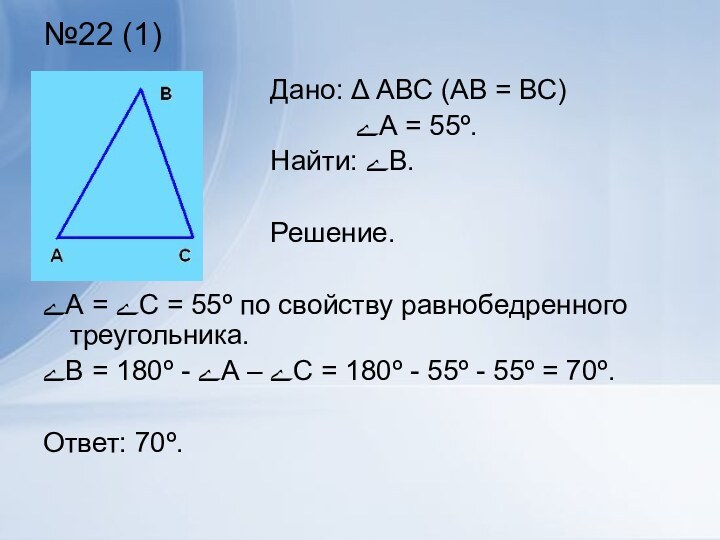
№22 (1)
ےА = ےС = 55º по свойству
равнобедренного треугольника.
ےВ = 180º - ےА – ےС =
180º - 55º - 55º = 70º.
Ответ: 70º.
Дано: Δ АВС (АВ = ВС)
ےА = 55º.
Найти: ےВ.
Решение.
Слайд 24
№23 (2)
По свойству равнобедренного треугольника:
ے А= ے
С. Таким образом,
ے А = ےС =
(180 – 120)/2 = 30º.
Ответ: 30 º.
Дано: Δ АВС (АВ = ВС)
ےВ = 120º.
Найти: ےА и ےС .
Решение.