Прямоугольная одномерная потенциальная яма
шириной a и
глубиной U0III. Притягивающий кулоновский потенциал (атом водорода)
U(r) =
0, r > a
-U0, r < a
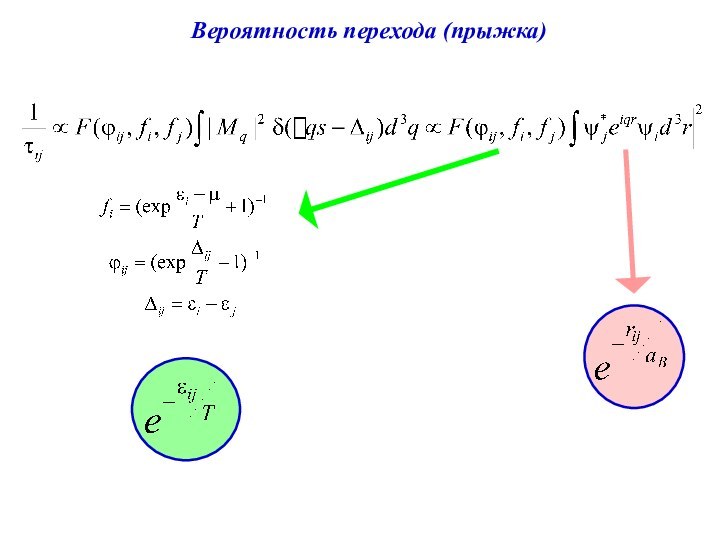
Общее определение:
при
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
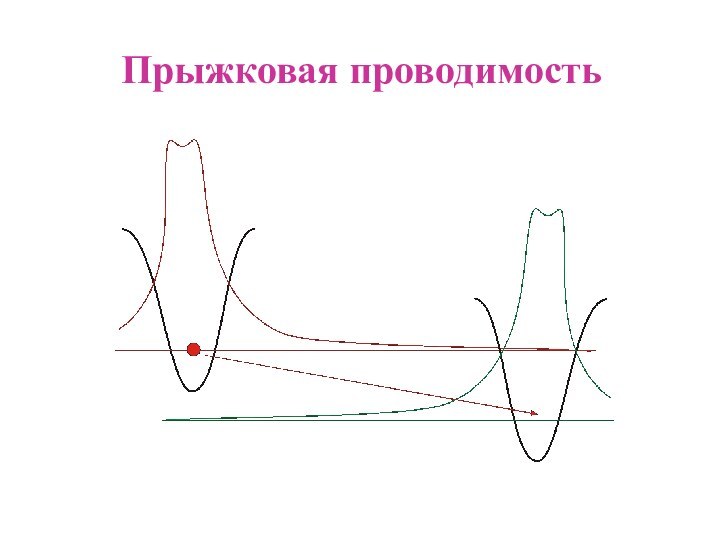







III. Притягивающий кулоновский потенциал (атом водорода)
U(r) =
0, r > a
-U0, r < a
Общее определение:
при
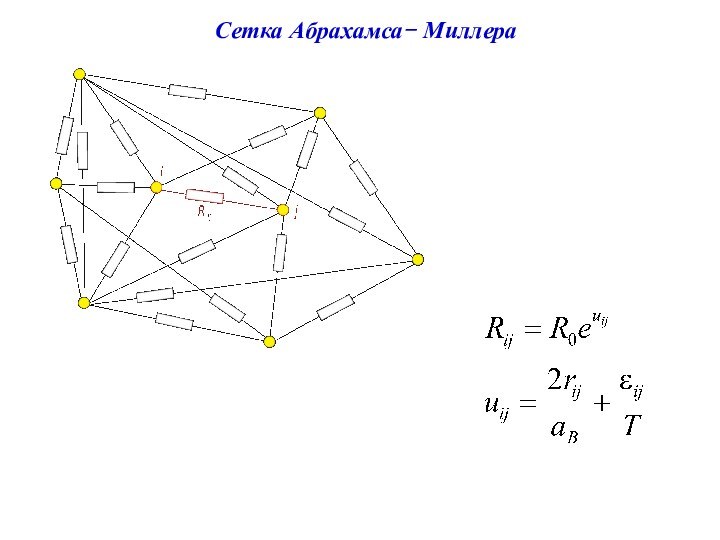
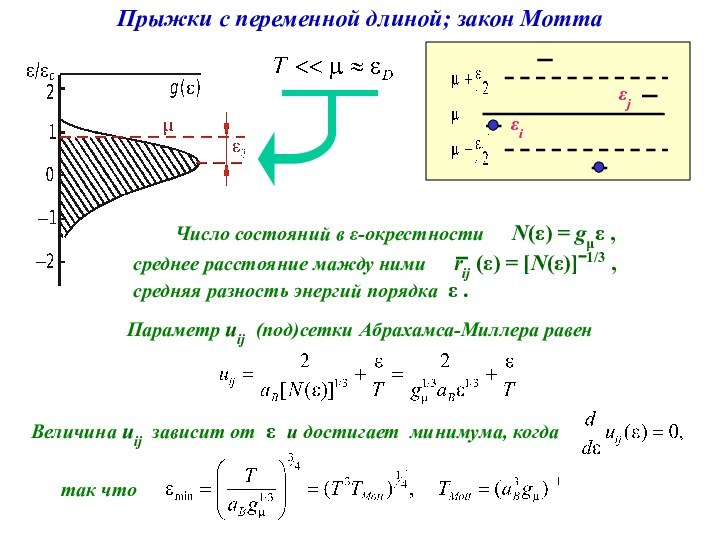
Параметр uij (под)сетки Абрахамса-Миллера равен
Величина uij зависит от e и достигает минимума, когда
так что
и сопротивление равно
Закон Мотта (продолжение)
Далее все стандартно
и сопротивление равно
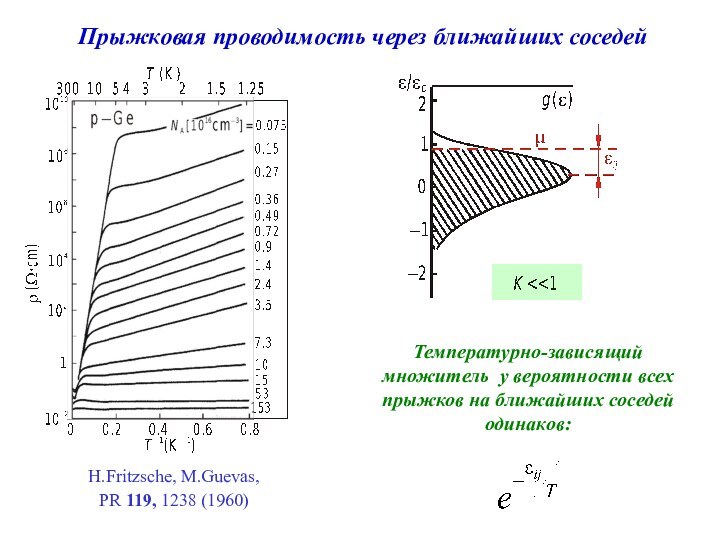
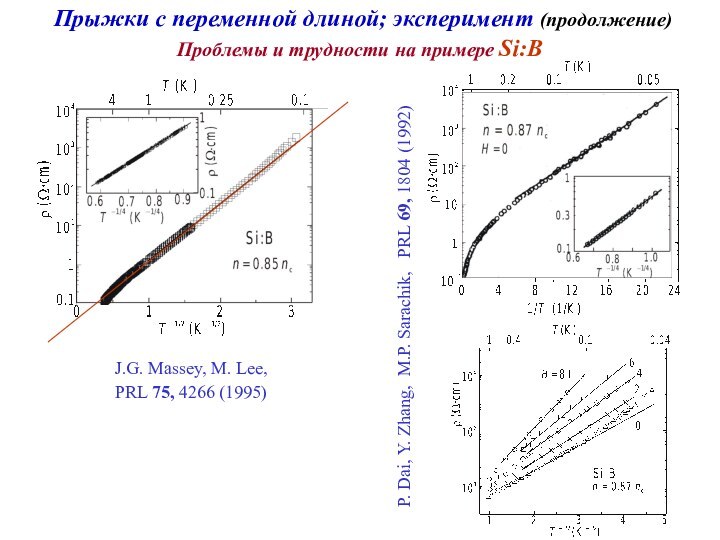
W.N. Shafarman, D.W.Koon, T.G. Castner,
PRB 40, 1216 (1989)