Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Свойства функций (9 класс)

Содержание

Вступительное слово.Дорогие друзья! Мы представляем Вашему вниманию презентацию для обучения и подготовке к экзамену по алгебре. Тема нашей работы «Свойства функций». В работе представлены те функции, которые изучаются в курсе алгебры 7, 8, 9 классов. Получить
Краткий электронный справочник. Авторы: Щербак Н. А., Морозов В. В. Вступительное слово.Дорогие друзья! Мы представляем Вашему вниманию презентацию для обучения и подготовке Выберите тему: Свойства функций Примеры построения Квадратичная функция.УХ-2-11214Пример:f (x) = х²а) Графиком функции является парабола;б) О(0;0) - вершина Степенная функция с натуральным показателем.Пример:f (x) = x³.а)Графиком функции является кубическая параболаб)График Линейная функция.1.D (f) = (- ∞;∞)2.E (f) = ( - ∞;∞)3.f (x) Прямая пропорциональность.Пример:f (x) = kx, k>0а)Графиком функции является прямая;б)График функции проходит через Обратная пропорциональность1.D (f) = ( - ∞;0) U (0;- ∞)2.E (f) = Функция у = √х1.D (f) = [0;∞)2.E (f) = [0;∞)3.f (x) = Пример построения графика квадратичной функции. F(x)= 2x² + 8x +21) Ветви Пример построения графика линейной функции yx1205Пример: y=2x+1Если x=0, то y=2 • 0+1=1Если x=2, то y=2•2+1=5 Обратная пропорциональность и ее графикПример: y=6/x-2-3-6-1-2-3-6-2-3123yx0 49162340Если x=4, то y=√4=2 Построение графика функции y=√x yx Построение графика прямой пропорциональности.f (x) = x, к = 1Пример: y=1 • 2=2y=1 • 3=3yx02332 Построение графика степенной функции с натуральным показателем.f (x) = x³Пример: y=2³=8y= (-2)³ = -8yx022-2-2 авторы: Ю.Н. Макарычев Н.Г. Миндюк К.И. Нешков С.Б. Суворовагод издания: 2005Издательство: Просвещение.Кликните Желаем успехов.Спасибо за внимание.All rights reserved ©
Слайды презентации

Слайд 2 Вступительное слово.
Дорогие друзья! Мы представляем Вашему вниманию презентацию

Вступительное слово.Дорогие друзья! Мы представляем Вашему вниманию презентацию для обучения и

для обучения и подготовке к экзамену по алгебре. Тема

нашей работы «Свойства функций». В работе представлены те функции, которые изучаются в курсе алгебры 7, 8, 9 классов. Получить дополнительную информацию вы можете по ссылке>>

Желаем успехов.

Слайд 3 Выберите тему:

Выберите тему:

Слайд 4 Свойства функций

Свойства функций

Слайд 5 Примеры построения

Примеры построения

Слайд 6 Квадратичная функция.


У
Х
-2
-1
1
2
1
4
Пример:
f (x) = х²
а) Графиком функции является

Квадратичная функция.УХ-2-11214Пример:f (x) = х²а) Графиком функции является парабола;б) О(0;0) -

парабола;
б) О(0;0) - вершина параболы;
в) х=0 – ось симметрии

параболы.
г) График функции расположен в I и II координатных четвертях.

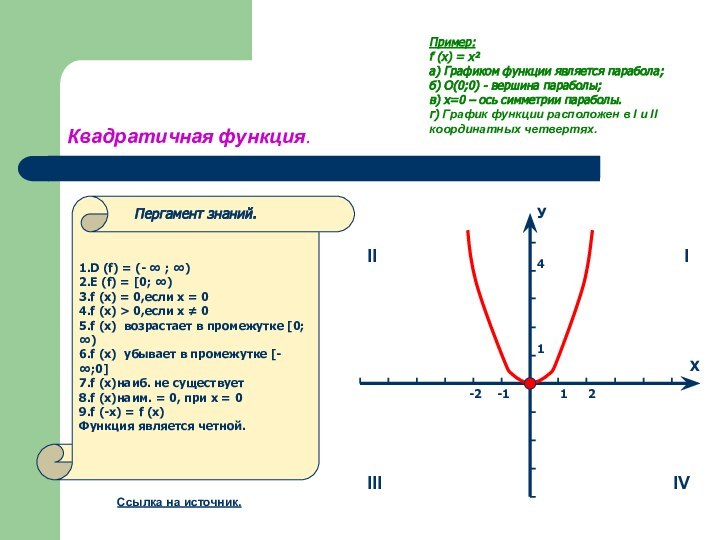
1.D (f) = (- ∞ ; ∞)
2.E (f) = [0; ∞)
3.f (x) = 0,если х = 0
4.f (х) > 0,если х ≠ 0
5.f (x) возрастает в промежутке [0; ∞)
6.f (x) убывает в промежутке [- ∞;0]
7.f (x)наиб. не существует
8.f (x)наим. = 0, при х = 0
9.f (-x) = f (x)
Функция является четной.


Пергамент знаний.

Ссылка на источник.

IV

II

I

III

Слайд 7 Степенная функция с натуральным показателем.
Пример:
f (x) = x³.
а)Графиком

Степенная функция с натуральным показателем.Пример:f (x) = x³.а)Графиком функции является кубическая

функции является кубическая парабола
б)График функции проходит через точку (0;0)


в)График функции расположен в I и III координатных четвертях.


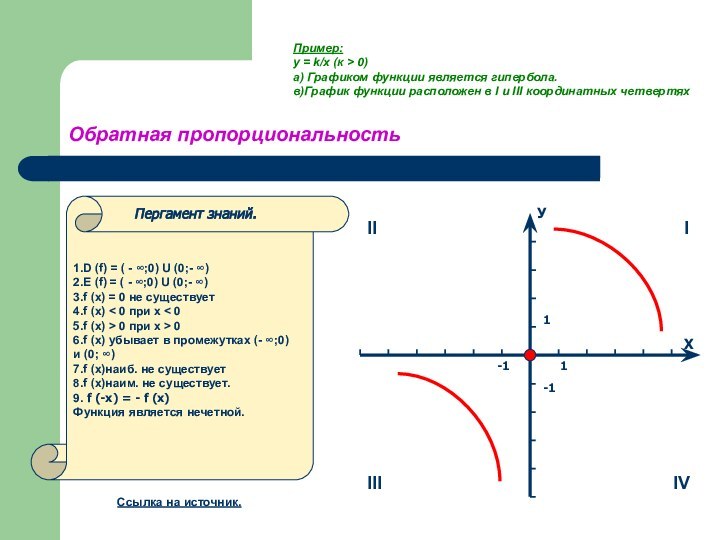
1.D (f) = (- ∞ ; ∞)
2.E (f) = ( - ∞ ; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, если x > 0
5.f (x) < 0, если х < 0
6.f (x) возрастает в промежутке (- ∞; ∞)
7.f (х)наиб. не сущ.
8.f (х)наим. не сущ.
9.f (-x) = - f (x)
Функция является нечетной.

Пергамент знаний.

У

Х


-1

1

1

-1

Ссылка на источник.

II

I

III

IV

Слайд 8 Линейная функция.
1.D (f) = (- ∞;∞)
2.E (f) =

Линейная функция.1.D (f) = (- ∞;∞)2.E (f) = ( - ∞;∞)3.f

( - ∞;∞)
3.f (x) = 0 ,при x= -0.5
4.f

(x) > 0, если x > -0,5
5.f (x) < 0, если x < -0,5
6.f (x) возрастает на всей области определения
8.f (x)наиб. не сущ.
9.f (x)наим. не сущ.
10.Функция не является ни четной, ни нечетной.

Пергамент знаний.

Ссылка на источник.

У

Х

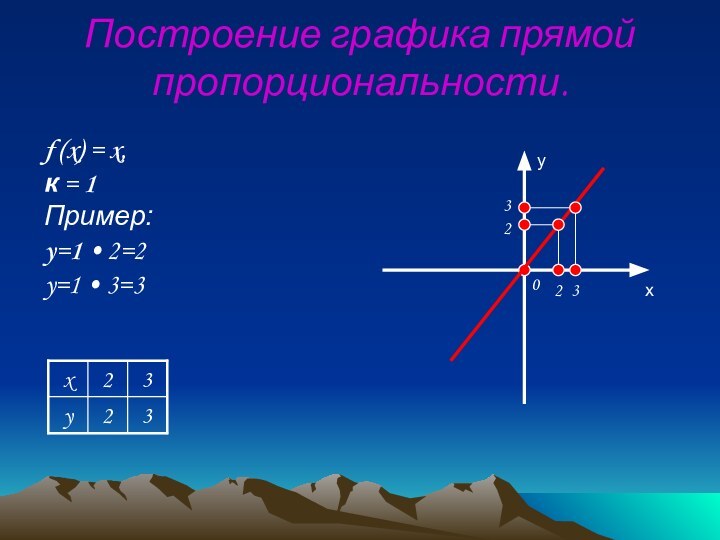
Пример:
f (x)= 2x + 1
а) Графиком функции является прямая,
б)График функции проходит через точки (-0,5;0) и (0;1)



-0.5

1

II

I

III

IV

Слайд 9 Прямая пропорциональность.
Пример:
f (x) = kx, k>0
а)Графиком функции является

Прямая пропорциональность.Пример:f (x) = kx, k>0а)Графиком функции является прямая;б)График функции проходит

прямая;
б)График функции проходит через точку (0;0)
в)График функции расположен в

I и III координатных четвертях.

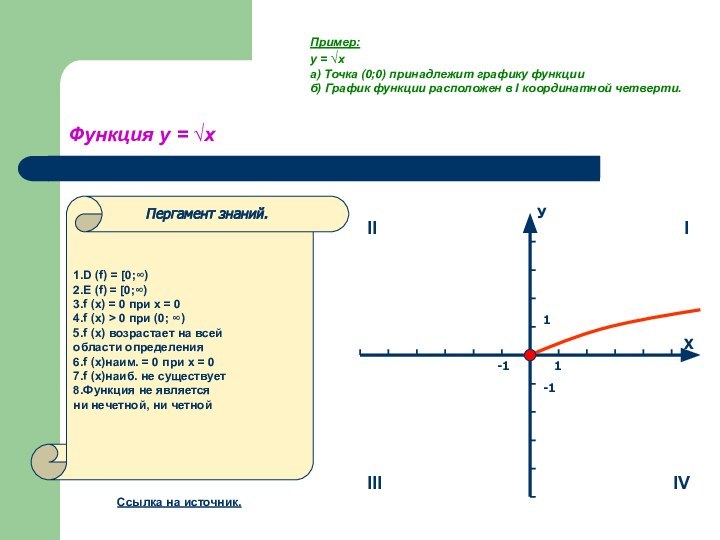
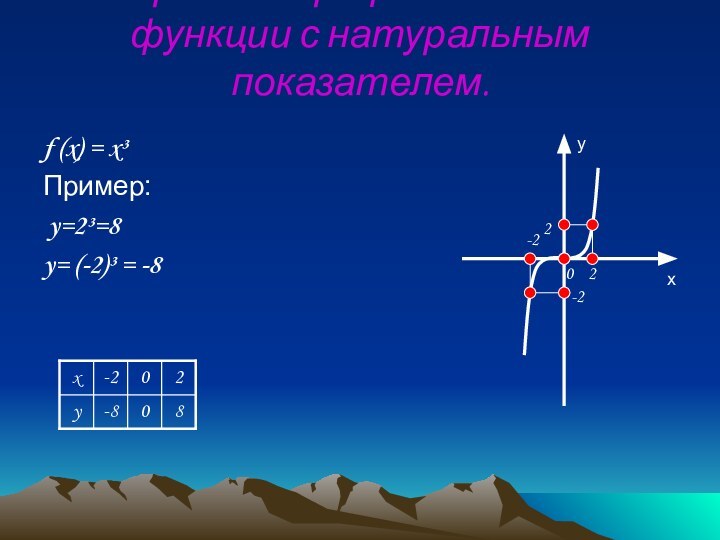
1.D (f) = (- ∞; ∞)
2.Е (f) = ( - ∞; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, при x > 0
5.f (x) < 0, при x < 0
6.f (x) возрастает в промежутке
(- ∞; ∞), т.е. на всей числовой прямой.
7.f (x)наиб.- не сущ.
8.f (x)наим.- не сущ.
9.f (-x) = - f (x)
Функция является нечетной.


Пергамент знаний.

Ссылка на источник.

III

IV

II

I

У

Х


Слайд 10 Обратная пропорциональность
1.D (f) = ( - ∞;0) U

Обратная пропорциональность1.D (f) = ( - ∞;0) U (0;- ∞)2.E (f)

(0;- ∞)
2.E (f) = ( - ∞;0) U (0;-

∞)
3.f (x) = 0 не существует
4.f (x) < 0 при х < 0
5.f (x) > 0 при x > 0
6.f (x) убывает в промежутках (- ∞;0)
и (0; ∞)
7.f (x)наиб. не существует
8.f (x)наим. не существует.
9. f (-x) = - f (x)
Функция является нечетной.

Пергамент знаний.

Ссылка на источник.

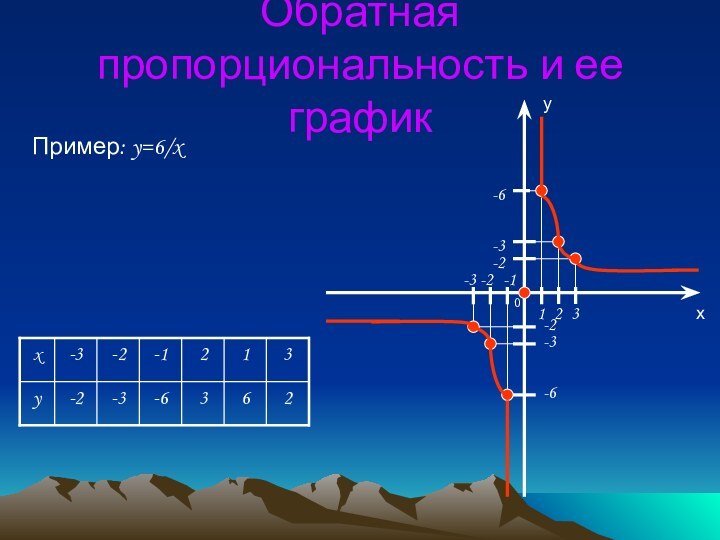
Пример:
y = k/x (к > 0)
а) Графиком функции является гипербола.
в)График функции расположен в I и III координатных четвертях


У

Х

II

III

I

IV


1

-1

1

-1

Слайд 11 Функция у = √х
1.D (f) = [0;∞)
2.E (f)

Функция у = √х1.D (f) = [0;∞)2.E (f) = [0;∞)3.f (x)

= [0;∞)
3.f (x) = 0 при x = 0
4.f

(x) > 0 при (0; ∞)
5.f (x) возрастает на всей
области определения
6.f (x)наим. = 0 при х = 0
7.f (x)наиб. не существует
8.Функция не является
ни нечетной, ни четной

Пергамент знаний.

Ссылка на источник.

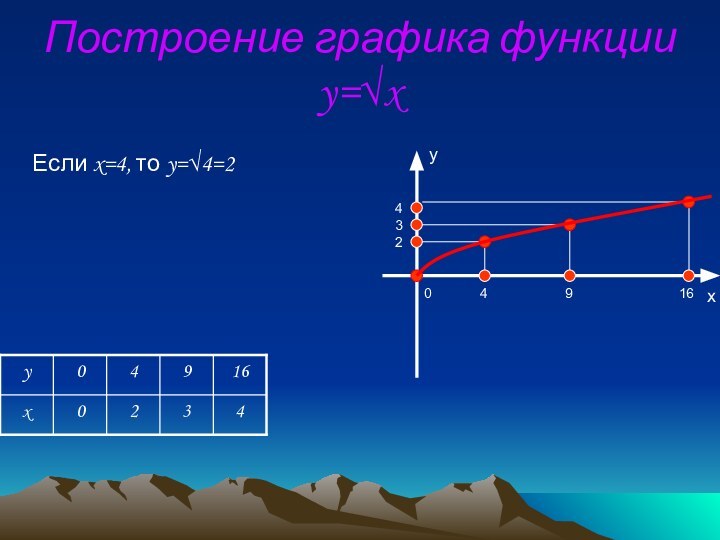
Пример:
y = √x
а) Точка (0;0) принадлежит графику функции
б) График функции расположен в I координатной четверти.



У

Х

II

I

III

IV

1

-1

1

-1

Слайд 12 Пример построения графика квадратичной функции.
F(x)= 2x² +

Пример построения графика квадратичной функции. F(x)= 2x² + 8x +21) Ветви

8x +2
1) Ветви
2) х = -8 ∕

2•2= -2
y = f(x ) = 2•(-2)² + 8•(-2)+2= -6
С (-2;-6)
3) х=-2 ( ось симметрии параболы)
4)




у

х


-2

-6







Слайд 13 Пример построения графика линейной функции


y
x
1
2
0
5
Пример: y=2x+1
Если x=0,

Пример построения графика линейной функции yx1205Пример: y=2x+1Если x=0, то y=2 • 0+1=1Если x=2, то y=2•2+1=5

то y=2 • 0+1=1
Если x=2, то y=2•2+1=5

Слайд 14 Обратная пропорциональность и ее график









Пример: y=6/x

-2
-3
-6
-1
-2
-3
-6
-2
-3
1
2
3
y
x
0

Обратная пропорциональность и ее графикПример: y=6/x-2-3-6-1-2-3-6-2-3123yx0

Слайд 15









4
9
16
2
3
4
0

Если x=4, то y=√4=2
Построение графика функции y=√x
y
x

49162340Если x=4, то y=√4=2 Построение графика функции y=√x yx

Слайд 16 Построение графика прямой пропорциональности.
f (x) = x,
к

Построение графика прямой пропорциональности.f (x) = x, к = 1Пример: y=1 • 2=2y=1 • 3=3yx02332

= 1
Пример:
y=1 • 2=2
y=1 • 3=3








y
x
0
2
3
3
2

Слайд 17 Построение графика степенной функции с натуральным показателем.
f (x)

Построение графика степенной функции с натуральным показателем.f (x) = x³Пример: y=2³=8y= (-2)³ = -8yx022-2-2

= x³
Пример:
y=2³=8
y= (-2)³ = -8











y
x
0
2
2
-2
-2

Слайд 18 авторы: Ю.Н. Макарычев Н.Г. Миндюк К.И. Нешков С.Б. Суворова
год издания: 2005
Издательство: Просвещение.
Кликните

авторы: Ю.Н. Макарычев Н.Г. Миндюк К.И. Нешков С.Б. Суворовагод издания: 2005Издательство:

на картинку, что бы перейти на Интернет ресурс, по

учебнику.
  • Имя файла: svoystva-funktsiy-9-klass.pptx
  • Количество просмотров: 236
  • Количество скачиваний: 2
- Предыдущая Тропические пустыни
Следующая - Бактерии

Похожие презентации

Презентация к уроку математики в 4 классе по теме Находим неизвестное. Презентация к уроку математики в 4 классе по теме Находим неизвестное. 127
ВЕСЕЛЫЙ СЧЕТ презентация по математике ВЕСЕЛЫЙ СЧЕТ презентация по математике 123
Презентация к уроку математики во 2 классе по теме Порядок выполнения действий. Скобки презентация к уроку по математике (2 класс) Презентация к уроку математики во 2 классе по теме Порядок выполнения действий. Скобки презентация к уроку по математике (2 класс) 114
Устный счет к урокам математики (2 кл) презентация к уроку по математике (2 класс) Устный счет к урокам математики (2 кл) презентация к уроку по математике (2 класс) 124
Число 3 Число 3 158
Логика Логика 89
Презентация по математике на тему Проект: Орнаменты на посуде Презентация по математике на тему Проект: Орнаменты на посуде 48
Умножение и деление на 10,100,1000,10000 план-конспект урока по математике (4 класс) Умножение и деление на 10,100,1000,10000 план-конспект урока по математике (4 класс) 158
Расширение понятия числа Расширение понятия числа 122
Прямой угол презентация урока для интерактивной доски по математике (3 класс) Прямой угол презентация урока для интерактивной доски по математике (3 класс) 145
Презентация к уроку Проверка умножения Презентация к уроку Проверка умножения 114
Презентация по математике на тему Сложение с числом 10 (1 класс) Презентация по математике на тему Сложение с числом 10 (1 класс) 89
Применение тестов на уроках математики Применение тестов на уроках математики 111
Ребусы по математике Ребусы по математике 112
Отношения. Пропорции.Подготовка к контрольной работе Отношения. Пропорции.Подготовка к контрольной работе 97
Презентация к уроку по математике для 6 класса на тему Твоя жизнь – твой выбор, или несколько цифр о здоровье Презентация к уроку по математике для 6 класса на тему Твоя жизнь – твой выбор, или несколько цифр о здоровье 119
Как люди учились считать Как люди учились считать 135
Презентация к уроку математики план-конспект занятия по математике (1 класс) по теме Презентация к уроку математики план-конспект занятия по математике (1 класс) по теме 103
Производная сложной функции Производная сложной функции 98
zadachi na umenshenie na neskolko edinits zadachi na umenshenie na neskolko edinits 119
Весёлые эксперименты опыты и эксперименты по математике (подготовительная группа) Весёлые эксперименты опыты и эксперименты по математике (подготовительная группа) 181
Презентация по математике к юбилею С.Ф.Гоголева Презентация по математике к юбилею С.Ф.Гоголева 144
Двоичная система счисления Двоичная система счисления 102
Сложение и вычитание двузначных чисел 2 класс Сложение и вычитание двузначных чисел 2 класс 106
Это мы не проходили… Это мы не проходили… 108
Урок математики в 3 классе по теме Площадь фигуры. Единицы площади. план-конспект урока по математике (3 класс) Урок математики в 3 классе по теме Площадь фигуры. Единицы площади. план-конспект урока по математике (3 класс) 127
Презентация к уроку математики, 2 класс - Задачи на умножение презентация к уроку по математике (2 класс) Презентация к уроку математики, 2 класс - Задачи на умножение презентация к уроку по математике (2 класс) 97
Решение задач по математике 2 класс Решение задач по математике 2 класс 112
Презентация по математике Математическая шкатулка Презентация по математике Математическая шкатулка 115
Презентация к уроку математики в 1 классе по теме Уменьшаемое, вычитаемое презентация к уроку по математике (1 класс) Презентация к уроку математики в 1 классе по теме Уменьшаемое, вычитаемое презентация к уроку по математике (1 класс) 98