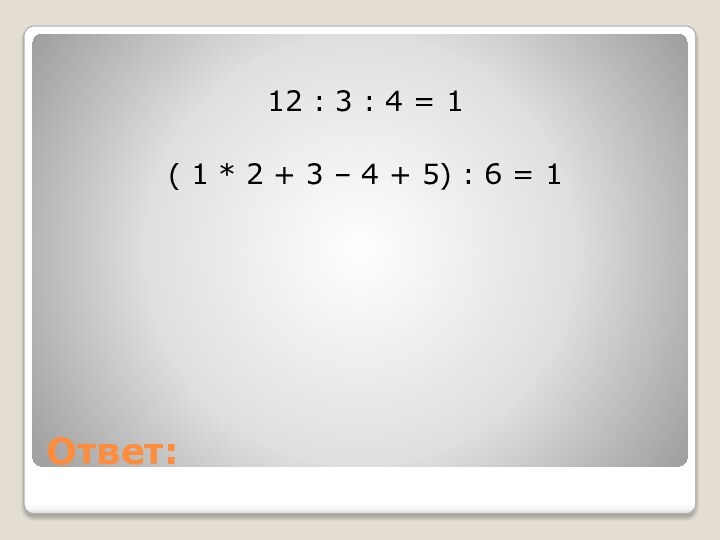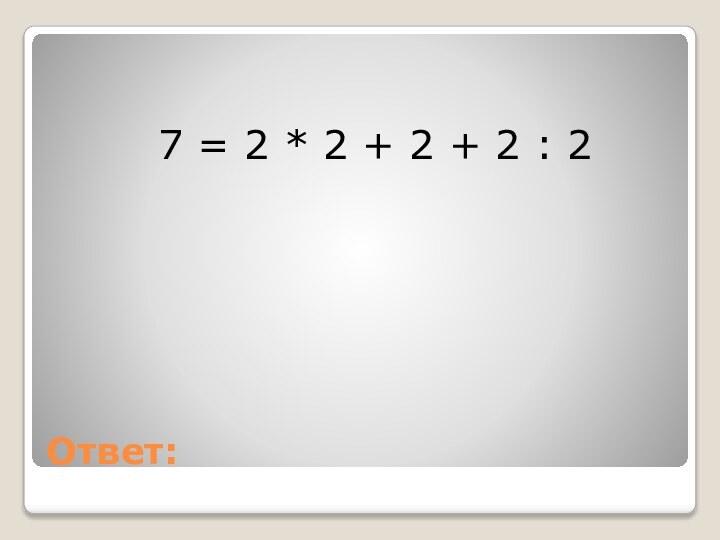Слайд 2
Немного из истории математики
Немало различных способов записи чисел
было создано людьми. В Древней Руси числа обозначали буквами
с особым знаком «Ɲ» (титло), который писали над буквой.
Первые девять букв обозначали единицы, следующие девять букв – десятки, а последние девять букв – сотни. Число десять тысяч называли словом «тьма». (Мы и теперь говорим: «народу – тьма тьмущая» )
Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли её у индусов. Поэтому цифры , которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы – « индийскими».
Эта система была введена в Европе примерно в 1120 году английским путешественником Аделардом. К 1600 году она была принята в большинстве стран мира.
Слайд 3
Много есть разных версий об истории возникновения начертаний
цифр. Пушкин А.С. Считал, что все арабские цифры произошли
от магического квадрата. Вот посмотрите.
Слайд 4
Наряду с развитием науки о числах появились и
различные числовые суеверия. Пифагорейцы, изучая окружающую природу, пришли к
идее, каждому явлению природы, каждой вещи поставить в соответствие число. По их мнению «вещи суть копии чисел, числа суть начала вещей».
Даже каждого человека можно закодировать числом. И за каждым числом прячется тайна.
Давайте и мы каждый узнаем сейчас какое наше число.
Слайд 5
А – 1, Б – 2, В –
6, Г – 3, Д – 4,
Е – 5, Ж – 2, З – 7, И – 1, К – 2, Л – 2, М – 4, Н – 5, О – 7, П – 8, Р – 2, С – 3, Т – 4, У – 6, Ф – 8 , Х – 5, Ц – 3, Ч – 7, Ш -2, Щ – 9, Ы – 1, Э – 6, Ю – 7, Я – 2.
Слайд 6
Ч и с л о 1
Получите единицу из
каждой следующей группы чисел:
1 2
3 4 = 1
1 2 3 4 5 6 = 1
Слайд 7
Ответ:
12 : 3 : 4 = 1
( 1
* 2 + 3 – 4 + 5) :
6 = 1
Слайд 8
Число 2
С помощью пяти двоек и знаков действий
можно представить любое число от 1 до 9:
1 =
2 +2 -2 - 2 : 2
2 = 2 +2 +2 - 2 - 2
3 = 2 + 2 - 2 + 2 : 2
4 = 2 * 2 * 2 - 2 * 2
5 = 2 + 2 + 2 - 2 : 2
6 = 2+ 2 + 2 + 2 - 2
Слайд 9
Задание:
7 = 2 * 2 * 2 *
2 * 2
8 = 2* 2 * 2 *
2 * 2
9 = 2 * 2 * 2 * 2 * 2
Слайд 14
Число 3
С помощью четырёх троек можно записать
все числа от 1 до 10
1 = 33
: 33, 2 = 3:3 + 3:3, 3 = (3+3+3):3,
4 = 3* 3+3:3, 5 = 3+3-3:3, 6 = 3+3+3-3,
7 = 3:3+3+3, 8 = 3*3 -3:3, 9 =3*3*3:3,
10 =3:3+3*3
Слайд 15
Число 4
1 + 2 + 3 + 4
= 10
Посмотрите, как можно написать все числа от
1 до 10 с помощью четырёх четвёрок и знаков действий
1 = 44:44, 2 = 4:4 + 4:4, 3 = 4+4+4 :4,
4 = 4+ 4*(4 – 4), 5 = 4*4+4:4, 6 = 4+4:4+4,
7 = 4+4 -4:4, 8 =4*4 -4-4, 9 = 4 +4+4:4,
10 =44-4:4.
Слайд 17
Число 6
Если число 6 умножить на 9,
полученное произведение умножить на 12345679, то получится 666666666 =
6* 111111111.
Точно также можно умножить 5 на 9 и то же получить очень интересное число.
Какое это число?
Слайд 18
Задумайте число. Удвойте его и к полученному произведению
прибавить 5. Результат умножьте на 5 и к произведению
прибавьте удвоенную пятёрку. Сумму умножьте на удвоенную пятёрку.
Слайд 19
Число 7
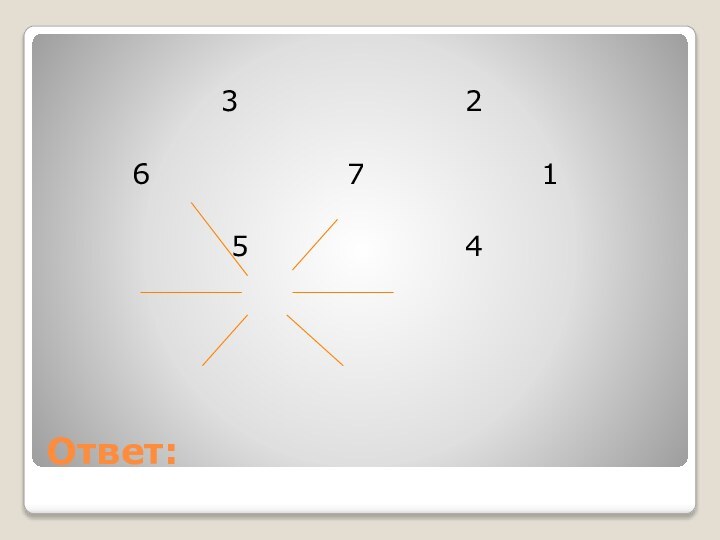
Решите задачу:
Расставьте числа 1,2,3,4,5 и 6 по
вертикали и в центре шестиугольника так, чтобы сумма трёх
чисел, лежащих на каждой из диагоналей, равнялась 14.
7
Слайд 21
Число 49 есть квадрат числа 7, т.е. 49=7*7.
Найдите
закономерность в получении квадратов чисел: 67, 667, 6667.
Слайд 22
Число 8
Если число 8 будем умножать
на числа от 1 до 5, то получим в
произведении такие числа, сумма цифр которых всё время уменьшаетя.
8* 1 = 8 8+0=8
8*2 =16 1+6=7
8*3 = 24 2+4+6
8*4 = 32 3+2=5
8*5 = 40 4+0=4
Слайд 23
Задача:
Напишите 1000 восемью восьмёрками, употребляя знаки действий.
1000 =
888 + 88 + 8 + 8 + 8
Слайд 25
Число 9
Умножим все числа от 1 до 10
на 9. Смотрите,
Всегда получим число, сумма цифр которого есть
9 .
9 * 1 = 9 9 + 0 = 9
9 * 2 = 18 1 + 8 = 9
9 * 3 = 27 2 + 7 = 9
9 * 4 = 36 3 + 6 = 9
9 * 5 =45 4+5 =9
Слайд 26
Задача:
Если написать произвольное двузначное число, затем переставить цифры
этого числа, т.е. получить обратное число, и вычесть из
большего меньшее, то сумма цифр, полученной разности всегда будет равна 9, а разность, следовательно, будет делиться на 9.
Слайд 27
Головоломки:
У семерых братьев по одной сестре, много ли
сестёр?
Ты да я, да мы с тобой. Много ли
нас стало?
Сын с отцом, да дедушка с внуком. Сколько всего?
Шли гурьбой: тёща с зятем, да муж с женой, мать с дочерью, да бабушка с внучкой, да дочь с отцом. Много ли всех?
Летела стая тетеревов, села на деревья: по двое на дерево сядут – одно дерево лишнее, по одному сядут – один тетерев лишний. Сколько тетерев и сколько деревьев?
Слайд 28
Итак, выслушав всех выступающих, мы сделали вывод:
– божественное
число;
- духочувсвенное, храброе число;
- символ совершенства;
-
символ силы;
- символ правосудия;
- символ течения времени;
-священное число;
-символ убывания,
-число премудрости.