- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема о вписанном угле
Содержание
- 2. Какая дуга называется полуокружностью?Какой угол называется центральным?Как
- 3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. АВСК12=+Повторение
- 4. ОТеорема. Вписанный угол измеряется половиной
- 5. ОАСВ2 случайD
- 6. ОАСВ3 случайD
- 7. Решить устно задачуНайдите вписанный угол АВС, если
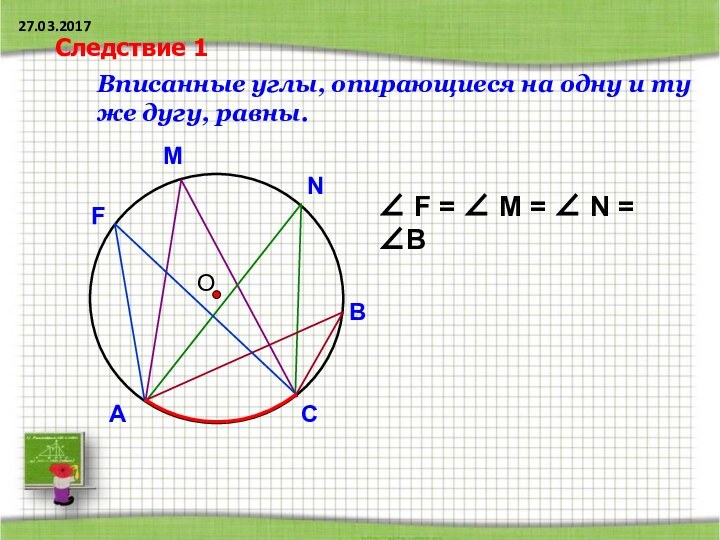
- 8. ОВписанные углы, опирающиеся на одну и ту
- 9. ОВписанный угол, опирающийся на полуокружность – прямой.Следствие 2ВА
- 10. Теорема об отрезках пересекающихся хорд
- 11. Скачать презентацию
- 12. Похожие презентации
Какая дуга называется полуокружностью?Какой угол называется центральным?Как находится дуга, если она меньше полуокружности?Как находится дуга, если она больше полуокружности?







Слайд 2
Какая дуга называется полуокружностью?
Какой угол называется центральным?
Как находится
дуга, если она меньше полуокружности?
больше полуокружности?
Слайд 3
Внешний угол треугольника равен сумме
двух углов треугольника,
не смежных с ним.
А
В
С
К
1
2
=
+
Повторение
Слайд 4
О
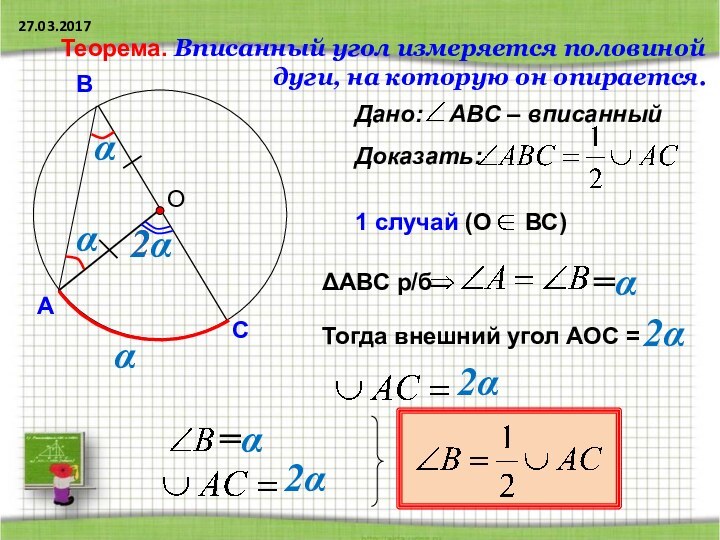
Теорема. Вписанный угол измеряется половиной
дуги, на которую он опирается.
2
2
=
2
Тогда внешний угол АОС =
Слайд 7
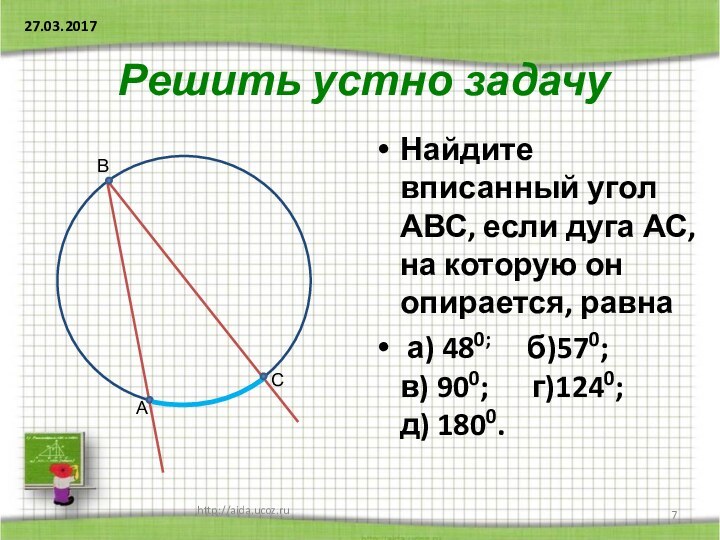
Решить устно задачу
Найдите вписанный угол АВС, если дуга
АС, на которую он опирается, равна
а) 480;
б)570; в) 900; г)1240; д) 1800.http://aida.ucoz.ru
А
В
С
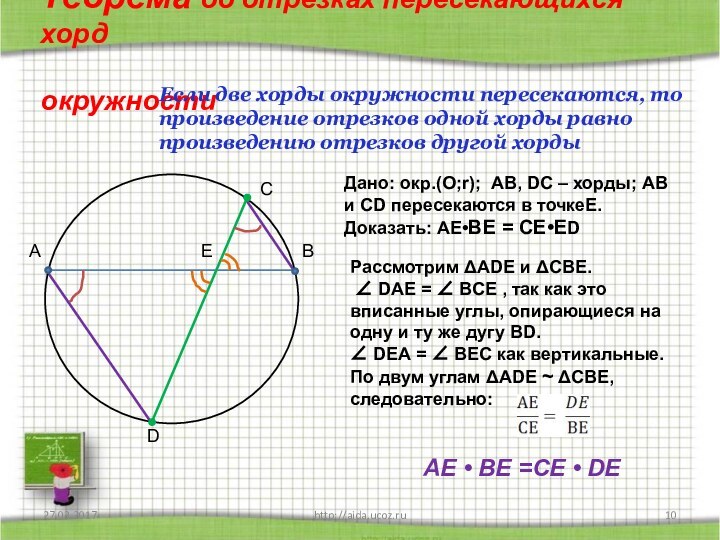
Слайд 10 Теорема об отрезках пересекающихся хорд
окружности
http://aida.ucoz.ru
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды
А Е В
С
D
Дано: окр.(О;r); АВ, DC – хорды; АВ и СD пересекаются в точкеЕ.
Доказать: АЕ•ВЕ = СЕ•ЕD
Рассмотрим АDЕ и СВЕ.
DАЕ = ВСЕ , так как это вписанные углы, опирающиеся на одну и ту же дугу ВD.
DЕА = ВЕС как вертикальные.
По двум углам АDЕ СВЕ, следовательно:
АЕ • ВЕ =СЕ • DE