Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Базовые понятия математической статистики

Содержание

Описательная статистика Локализация Среднее значениеМедианаМодаДисперсия ПерцентильМежквартильный размахРазмах признакаДисперсияСтандартное отклонение Коэффициент вариации
Базовые понятия математической статистики (2) Описательная статистика Локализация Среднее значениеМедианаМодаДисперсия ПерцентильМежквартильный размахРазмах признакаДисперсияСтандартное отклонение Коэффициент вариации Среднее значениеMean (англ.)Обозначение – М Формула = ∑x/n Медиана (1) Median (англ.)Обозначение: MеМедиана делит ряд на ДВЕ равные частиКак найти: Медиана (1) Медиана для чётного ряда – выбрать срединное Мода (1)Mode (англ.)Обозначение MoМода - это самое часто встречающееся значение в шкале Мода (2)Найдите наиболее частое значение в представленной шкале Перцентиль (1)Перцентиль указывает как данные распределены от минимального значения к максимальномуФормула расчета Перцентиль (2)Например, в ряду 2,4,5,6,7,9,10 25 перцентиль: i=25, n=7(25/100) × (n+1)= (25/100) Перцентиль (3)25 –й перцентиль – первый квартиль50 –й перцентиль – второй квартиль75 Размах признакаРазница между наблюдением с минимальным значением и максимальнымПример: ВесРазмах= 100-60=40 Стандартное отклонение (1)Измерение того как среднее значение представляет данныеМалое стандартное отклонение указывает 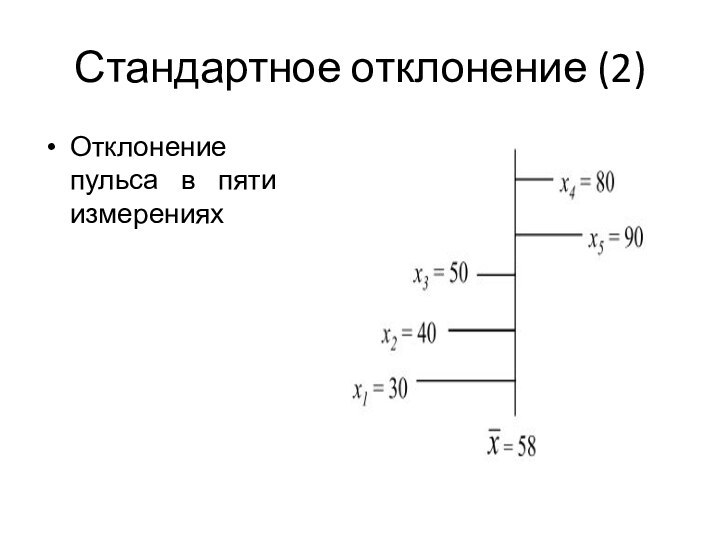Стандартное отклонение (2)Отклонение пульса в пяти измерениях Стандартное отклонение (3) Стандартное отклонение (4) 9( Стандартное отклонение (5) Степени свободыКоличество наблюдений варьирующихся свободно Внутри всех значений n свободно варьируются только Коэффициент вариациихарактеристика стандартного отклонения < 10% малый к.в.10-20% средний к.в.>20% высокий к.в.
Слайды презентации

Слайд 2 Описательная статистика
Локализация
Среднее значение
Медиана
Мода
Дисперсия
Перцентиль
Межквартильный размах
Размах признака
Дисперсия
Стандартное отклонение

Описательная статистика Локализация Среднее значениеМедианаМодаДисперсия ПерцентильМежквартильный размахРазмах признакаДисперсияСтандартное отклонение Коэффициент вариации


Коэффициент вариации

Слайд 3 Среднее значение
Mean (англ.)
Обозначение – М
Формула = ∑x/n

Среднее значениеMean (англ.)Обозначение – М Формула = ∑x/n

Слайд 4 Медиана (1)
Median (англ.)
Обозначение: Mе
Медиана делит ряд на

Медиана (1) Median (англ.)Обозначение: MеМедиана делит ряд на ДВЕ равные частиКак

ДВЕ равные части
Как найти: проранжировать значения от минимального к

максимальному и выбрать стединное

Слайд 5 Медиана (1)
Медиана для чётного ряда –

Медиана (1) Медиана для чётного ряда – выбрать срединное

выбрать срединное значение из

ранжированного ряда

Пример: 1,5,2,8,7
Ранжир.: 1,2,5,7,8
Me=5

Медиана для нечетного ряда – суммировать два срединных значения и разделить на два

Пример: 1,5,10,2,8,7
Ранжир.: 1,2,5,7,8,10
Me=(5+7)/2=6

Слайд 6 Мода (1)
Mode (англ.)
Обозначение Mo
Мода - это самое часто

Мода (1)Mode (англ.)Обозначение MoМода - это самое часто встречающееся значение в шкале

встречающееся значение в шкале

Слайд 7 Мода (2)
Найдите наиболее частое значение в представленной шкале

Мода (2)Найдите наиболее частое значение в представленной шкале

Слайд 8 Перцентиль (1)
Перцентиль указывает как данные распределены от минимального

Перцентиль (1)Перцентиль указывает как данные распределены от минимального значения к максимальномуФормула

значения к максимальному
Формула расчета i % = (i/100) ×

(n+1)

Слайд 9 Перцентиль (2)
Например, в ряду 2,4,5,6,7,9,10
25 перцентиль: i=25,

Перцентиль (2)Например, в ряду 2,4,5,6,7,9,10 25 перцентиль: i=25, n=7(25/100) × (n+1)=

n=7
(25/100) × (n+1)= (25/100) × (7+1)= 2
25% =4


В ряду 2,4,5,6,7,9
25 перцентиль: i=25, n=6
(25/100) × (n+1)= (25/100) × (6+1)= 1,76
25% =4 , т.к место под номером 1,76 между значениями «2» и «4» и ближе к «4»

Слайд 10 Перцентиль (3)
25 –й перцентиль – первый квартиль
50 –й

Перцентиль (3)25 –й перцентиль – первый квартиль50 –й перцентиль – второй

перцентиль – второй квартиль
75 –й перцентиль – третий квартиль


В

ряду : 2,4,5,6,7,9,10
25 –й перцентиль – 4
50 –й перцентиль – 6
75 –й перцентиль – 9



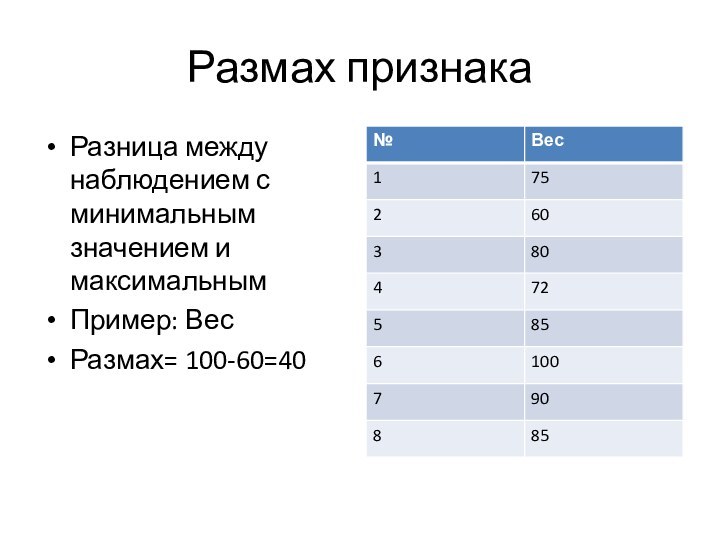
Слайд 11 Размах признака
Разница между наблюдением с минимальным значением и

Размах признакаРазница между наблюдением с минимальным значением и максимальнымПример: ВесРазмах= 100-60=40

максимальным
Пример: Вес
Размах= 100-60=40

Слайд 12 Стандартное отклонение (1)
Измерение того как среднее значение представляет

Стандартное отклонение (1)Измерение того как среднее значение представляет данныеМалое стандартное отклонение

данные
Малое стандартное отклонение указывает на то, что данные близки

к среднему
Большое стандартное отклонение указывает на то, что данные далеки от среднего значения


Слайд 13 Стандартное отклонение (2)
Отклонение пульса в пяти измерениях

Стандартное отклонение (2)Отклонение пульса в пяти измерениях

Слайд 14 Стандартное отклонение (3)

Стандартное отклонение (3)

Слайд 15 Стандартное отклонение (4) 9(

Стандартное отклонение (4) 9(

Слайд 16 Стандартное отклонение (5)

Стандартное отклонение (5)

Слайд 17 Степени свободы
Количество наблюдений варьирующихся свободно
Внутри всех значений

Степени свободыКоличество наблюдений варьирующихся свободно Внутри всех значений n свободно варьируются

n свободно варьируются только (n-1), оставшееся значение неизменно
(n-1)

значения изменяются т.о. именно им присвоена степень свободы

  • Имя файла: bazovye-ponyatiya-matematicheskoy-statistiki.pptx
  • Количество просмотров: 100
  • Количество скачиваний: 0
- Предыдущая Н.С. Лесков
Следующая - Системы, основанные на знаниях

Похожие презентации

Совместые действия с десятичными дробями Совместые действия с десятичными дробями 118
Действия с многозначными числами (4 класс) Действия с многозначными числами (4 класс) 120
Презентация методической разработки проекта Ох, уж эти сказки с мастер классом Презентация методической разработки проекта Ох, уж эти сказки с мастер классом 130
Признаки делимости натуральных чисел Признаки делимости натуральных чисел 125
Женщины - математики Женщины - математики 124
урок повторение. Сложение и вычитание от 20 до 100 презентация к уроку по математике (2 класс) урок повторение. Сложение и вычитание от 20 до 100 презентация к уроку по математике (2 класс) 47
Разработка конспекта занятия по математическому развитию по теме Знакомство с календарем план-конспект занятия по математике (старшая группа) по теме Разработка конспекта занятия по математическому развитию по теме Знакомство с календарем план-конспект занятия по математике (старшая группа) по теме 130
Түзу мен жазықтық арасындағы бұрыш Түзу мен жазықтық арасындағы бұрыш 131
Структура курса Структура курса 100
Презентация к уроку математики во 2 классе по теме Периметр презентация к уроку по математике (2 класс) по теме Презентация к уроку математики во 2 классе по теме Периметр презентация к уроку по математике (2 класс) по теме 95
Решай, считай, отгадвыай Решай, считай, отгадвыай 96
chislo i tsifra 1 chislo i tsifra 1 101
Треугольники. Третий признак равенства Треугольники. Третий признак равенства 89
Сложение и вычитание Сложение и вычитание 102
Число 1. цифра 1 Число 1. цифра 1 196
Куб 5-6 класс Куб 5-6 класс 107
Формы и системы оплаты труда Формы и системы оплаты труда 241
Презентация к уроку №80 по математике Что узнали? Чему научились?, 2 класс УМК Школа России презентация к уроку по математике (2 класс) Презентация к уроку №80 по математике Что узнали? Чему научились?, 2 класс УМК Школа России презентация к уроку по математике (2 класс) 228
Логарифмическая функция, её свойства и график Логарифмическая функция, её свойства и график 143
Н Н 114
Конспект урока математики во 2 классе по программе Школа России Уравнение. план-конспект урока по математике (2 класс) Конспект урока математики во 2 классе по программе Школа России Уравнение. план-конспект урока по математике (2 класс) 139
Презентация к уроку по теме Размещения Презентация к уроку по теме Размещения 129
Презентация Задачи на разностное сравнение презентация к уроку по математике (1 класс) Презентация Задачи на разностное сравнение презентация к уроку по математике (1 класс) 50
Улитка Паскаля Улитка Паскаля 156
Презентация по математике на тему Арифметические действия над числами (3 класс) Презентация по математике на тему Арифметические действия над числами (3 класс) 137
Мир цифр и чисел Мир цифр и чисел 124
Признаки делимости натуральных чисел Признаки делимости натуральных чисел 171
Презентация 5 класс Степень числа Презентация 5 класс Степень числа 129
Конспект урока план-конспект урока по математике (1 класс) Конспект урока план-конспект урока по математике (1 класс) 136
Страна отрицательных чисел Страна отрицательных чисел 104