Слайд 2
Автор проекта
Курманова Светлана,
ученица 9
«Б» класса
Научный руководитель проекта Сазонова Татьяна Фёдоровна,
учитель математики высшей
квалификационной категории
исследования:
собрать информацию об истории теоремы Пифагора и поисках различных
способов её доказательства;
разработать новые способы доказательства теоремы Пифагора.
Предмет исследования:
теорема Пифагора и различные способы её доказательства
Гипотезы исследования:
возможность применения теоремы об отрезках хорд, пересекающихся внутри круга, к доказательству теоремы Пифагора;
возможность существования доказательства теоремы Пифагора с опорой на теорему о пропорциональности отрезков секущей и отрезка касательной к окружности.
Слайд 4
Этапы реализации:
Поиск новых способов доказательства будет продолжен.
Форма представления
результатов:
Слайд 5
Содержание
Литература
Из биографии Пифагора
Из истории теоремы
Формулировки теоремы
Различные способы доказательства
теоремы Пифагора
Простейшее доказательство
Доказательство Эпштейна
Доказательство Бхаскари - Ачарна (XII век)
Доказательство
Нильсена
Доказательство Бетхера
Доказательство Перигаля
Доказательство Гутхейля
Доказательство IX века н.э.
Доказательство методом дополнения
Доказательство Евклида
Доказательство Хоукинсa
Доказательство Вальдхейма
Доказательство основанное на теории подобия
Маленькая – маленькая сказка, где автор проекта приводит свои доказательства теоремы Пифагора
Слайд 6
Литература
Березин В. Я. Теорема Пифагора. Квант, №8, 1971
г.
Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона
и Греции. М., Учпедгиз, 1959 г.
Глейзер Г.И. История математики в школе. М., Просвещение,1982 г.
Еленьский Щ. По следам Пифагора. М., Учпедгиз, 1961 г.
Литцман В. Теорема Пифагора. М., Просвещение, 1960 г.
Скопец З.А. Геометрические миниатюры. М., Просвещение, 1990 г.
Феоктистов И. Геометрия до Евклида в очерках и задачах. М.,
Чистые пруды, 2005 г.
Слайд 7
Из биографии Пифагора
Великий учёный Пифагор родился около

570 г. до н.э. на острове Самосе. Отцом Пифагора
был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твёрдой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера.
Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окружённым толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввёл юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим учёным - Фалесом. Фалес советует ему отправиться за знаниями в Египет, что Пифагор и сделал.
Слайд 8
В 548 г. до н.э. Пифагор прибыл в

Навкратис - самосскую колонию, где было у кого найти
кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но, влекомый жаждой к знаниям, Пифагор преодолел все эти испытания, хотя, по данным раскопок, египетские жрецы не многому могли его научить, так как в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счёте и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой.
Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучиться. Но в 530 г. до н.э. Кир двинулся в поход против племён в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полураба, и он удалился в пещеры в окрестностях Самоса. Поликрат его преследует, и Пифагор вынужден переселиться в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество.
... Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, не останавливаясь перед поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей – они своими телами вымостили дорогу любимому учителю из горящего дома. Без своей школы и без своих учеников Пифагор затосковал и вскоре покончил жизнь самоубийством.
Но в различных источниках можно встретить и другие версии последних дней Пифагора.
Задача данного проекта - обратиться к истории теоремы Пифагора и различным способам её доказательства.
Слайд 9
Из истории теоремы
Исторический обзор начнём с Древнего
Китая.
Самое древнее китайское математико-астрономическое сочинение «Чжоу-би», написанное около 1100
г. до н.э., в первой главе содержит предложения, относящиеся к прямоугольному треугольнику, среди которых – и теорема Пифагора. В летописях отмечается, что Пифагорова тройка 3; 4; 5 была известна в Китае ещё около 2200 г. до н.э.
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
Причём формулировка следующего утверждения соответствует именно прямой, а не обратной теореме:
Слайд 10
Кантор (крупнейший немецкий историк математики) считает, что равенство

3 ² + 4 ² = 5² было известно уже египтянам еще
около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или "натягиватели верёвок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмем верёвку длиною в 12 линейных единиц и привяжем к ней по цветной полоске на расстоянии 3 единицы от одного конца и 4 единицы от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент: например, рисунки, изображающие столярную мастерскую. Но в том-то и дело, что для изготовления такого шаблона как раз и использовали идею гарпедонаптов.
Слайд 11
Соотношение между катетами и гипотенузой можно встретить у

вавилонян. В одном тексте, относимом ко времени царствования Хаммурапи,
т. е. к 2000 г. до н. э., приводится приближённое вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления сторон прямоугольного треугольника, по крайней мере, в некоторых случаях. Вавилоняне смогли найти такие «пифагоровы тройки», как 65; 72; 97 или 3456; 3367; 4825.
Читаем правило для построения прямого угла - перпендикуляра к направлению жертвенника: «К концам отрезка длиной 39 прикрепим концы верёвки длиной 51 с узлом на расстоянии 15 от одного из концов; держа за узел и , подтянув верёвку, получим прямой угол». Известная нам теорема Пифагора там имела следующую формулировку: «Квадрат диагонали прямоугольника равен сумме квадратов его большей и меньшей сторон. Квадрат на диагонали квадрата в два раза больше самого квадрата».
Теорема о квадрате гипотенузы встречается в священных древнеиндийских книгах «Сульва-сутра» («Правила верёвки») созданных в период с VII по IV веках до н.э.
Слайд 12
Как видим теорема эта была открыта практиками почти

за 600 лет до Пифагора. Но это ничуть не
умаляет его заслуги перед наукой.
В "Перечне математиков", приписываемом Евдему, о Пифагоре сказано так: "Как передают, Пифагор превратил занятие этой отраслью знания (геометрией) в настоящую науку, рассматривая её основы с высшей точки зрения и исследуя её теории менее материальным и более умственным образом".
Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:
"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но её систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."
Пифагору приписываются создание основ планиметрии, правил построения некоторых правильных многоугольников и многогранников, введение широкого и обязательного использования доказательств в геометрии, создание учения о подобии, и , наконец, доказательство теоремы о сторонах прямоугольного треугольника.
Интересна легенда, из которой мы узнаём, с какой страстью Пифагор изучал уже достигнутое в математике и совершал новые научные открытия.
вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя ,вслед.
Они не в силах свету помешать ,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Известна, например, легенда, рассказывающая нам о том, как Пифагор, сумевший доказать теорему, пришёл в неописуемый восторг и в благодарность богам принёс им в жертву 100 быков.
Немецкий писатель-романист Шамиссо с юмором пишет:
Слайд 14
Формулировки теоремы
У Евклида эта теорема гласит

(дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало XII в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Более строгой надо считать такую формулировку: «Если гипотенуза и катеты прямоугольного треугольника измерены одной и той же единицей длины, то квадрат числового значения длины гипотенузы равен сумме квадратов числовых значений длин катетов».
Слайд 15
Различные способы доказательства
теоремы Пифагора
На рисунке дан простейший равнобедренный прямоугольный треугольник АВС (закрашен серым цветом, АВ и ВС -катеты).
По данному рисунку я приведу два доказательства.
Если квадраты отложить в общую часть полуплоскостей с границами АВ и ВС, то сумма числовых значений площадей квадратов, построенных на катетах, равна 4SABC (квадраты совпали). Но и площадь квадрата, построенного на гипотенузе, тоже равна 4SABC
Если же квадраты отложить на сторонах во внешнюю область, то и в этом случае 2+2=4.
Теорема доказана.
Простейшее доказательство
B
C
A
Слайд 16
Доказательства методом разложения
Существует целый ряд доказательств теоремы

Пифагора, в которых квадраты, построенные на катетах и на
гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из квадратов, построенных на катетах. Во всех этих случаях для понимания идеи доказательства достаточно одного взгляда на чертёж. Древние индусские математики древности вообще ограничивались единственным словом: «Смотри!».
Но, безусловно, доказательство нельзя считать полным, пока мы не доказали равенства всех соответствующих друг другу частей.
В данном проекте даётся в основном обзор идей доказательства, но учитель всегда может у вас попросить доказать равенство соответствующих фигур.
Доказательство Эпштейна
Точки E, C и F лежат на одной прямой; это следует из несложных расчётов градусной меры угла ECF (он развёрнутый).
CD проводим перпендикулярно EF.
Продолжены вверх левая и правая стороны квадрата, построенного на гипотенузе, до пересечения с EF; продолжена сторона ЕА до пересечения с CD.
Соответственно равные треугольники одинаково пронумерованы.
Слайд 17
Доказательство Нильсена
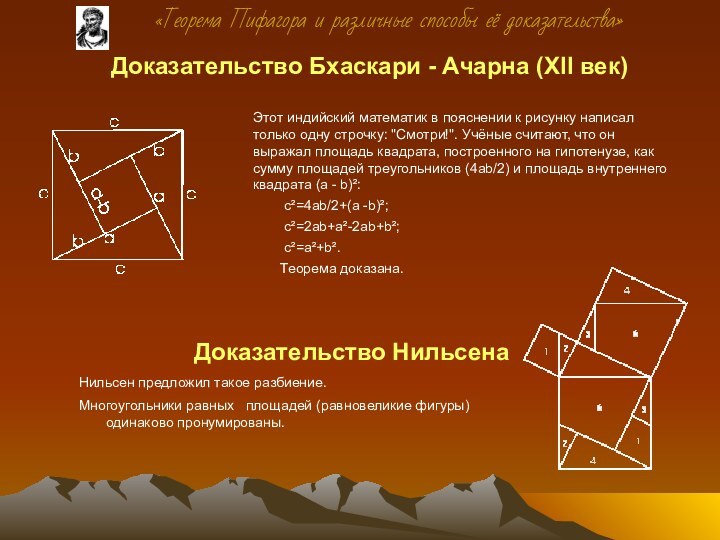
Нильсен предложил такое разбиение.
Многоугольники равных
площадей (равновеликие фигуры) одинаково пронумированы.
Этот индийский математик в пояснении
к рисунку написал только одну строчку: "Смотри!". Учёные считают, что он выражал площадь квадрата, построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь внутреннего квадрата (a - b)²:
c²=4ab/2+(a -b)²;
c²=2ab+a²-2ab+b²;
c²=a²+b².
Теорема доказана.
Доказательство Бхаскари - Ачарна (XII век)
Слайд 18
Доказательство Бетхера
Бетхер показывает, как
из треугольников, входящих в состав квадратов, построенных на катетах,
составить квадрат, построенный на гипотенузе.
Нижние треугольники 8 и 4 отодвигаем от фигуры 5-1, перераспределяем 7;6;2;3 так, как показано на втором рисунке.
Очень надеюсь, что вам самим захочется взять в руки ножницы, бумагу и составить эту композицию, чтобы убедиться ещё раз, что площадь квадрата, построенного на гипотенузе, действительно равна сумме площадей квадратов, построенных на катетах.
Слайд 19
Доказательство Перигаля
Перигаль через центр квадрата, построенного на большем
катете, проводит прямые: одну - параллельную и одну -
перпендикулярную гипотенузе.
В книгах фрагмент этого рисунка называют «колесо с лопастями».
Соответственно равные многоугольники одинаково пронумерованы.
Доказательство Гутхейля
Гутхейль предлагает такое наглядное расположение отдельных частей.
Попробуй закрасить соответственно равные части, и станет понятна идея математика. Вновь мы убеждаемся, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Если треугольник будет равнобедренным прямоугольным, то исчезнут части 5; 6 и 7
Слайд 20
Доказательство IX века н.э.
Математики

9 столетия новой эры разместили квадраты, построенные на катетах,
ступенями, один рядом с другим. Индусы называли эту композицию "стулом невесты". Построен и квадрат со стороной, равной гипотенузе. Общая часть двух квадратов, построенных на катетах, и квадрата, построенного на гипотенузе, - неправильный заштрихованный шестиугольник 5. Присоединив к нему треугольники 1 ; 2 и ещё один маленький треугольничек, получим оба квадрата, построенные на катетах; если же к заштрихованной фигуре присоединить треугольники 3 и 4 (соответственно равные 1 и 2) и такой же маленький треугольник, то получим квадрат, построенный на гипотенузе
Мы с вами рассмотрели доказательства в которых квадрат, построенный на гипотенузе, и квадраты, построенные на катетах, складывались из соответственно равных непересекающихся фигур. Такие доказательства называются доказательствами при помощи сложения ("аддитивными доказательствами") или, чаще, доказательствами методом разложения. Математики IX века предлагали другое расположение квадратов.
Слайд 21
Доказательство методом дополнения
Поворотом плоскости
с центром в т.А на
«-90 градусов» четырёхугольник ACKJ совместим с четырёхугольником ADGВ. Площадь каждого из них соответственно половина площади шестиугольников ACBHKJ и ADEFGB.
От двух равных площадей нужно отнять равновеликие части (пары равных прямоугольных треугольников 1;2 и 1;3) так, чтобы в одном случае остались два квадрата, построенные на катетах, а в другом- квадрат, построенный на гипотенузе.
А если от равных чисел отнять равные числа, то и разности будут равны.
Слайд 22
Доказательство Евклида
В самом деле, треугольники ABD и BFC

равны по двум сторонам и углу между ними: FB = AB, BC = BD, а углы между ними равны как тупые углы со взаимно перпендикулярными сторонами.
SABD = 0,5S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=0,5S ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH.
Аналогично, если вы проведёте отрезок АЕ используете равенство треугольников ВСК и АСЕ, то докажете, что SJCEL=SACKG.
Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.
Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату АGКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе.
Слайд 23
Доказательство Хоукинсa
Хоукинс задаёт поворот плоскости по часовой
стрелке с центром в точке С на 90 градусов.
Тогда образом треугольника ВСА при этом повороте станет треугольник B’CA’ Проведём высоту В'D треугольника В'АВ. Выделим штриховкой невыпуклый четырёхугольник A'АВ'В. Его можно разложить или на два равнобедренных треугольника САA' и СВВ' ,или на два треугольника A'В'А и A'В'В.
SCAA'=b²/2 , SCBB'=a²/2
SA'AB'B=(a²+b²)/2
Треугольники A'В'А и A'В'В имеют общее основание A’B’=с и высоты DA и DB, поэтому :
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая два полученных выражения для вычисления площади одной и той же фигуры, получим:
a²+b²=c²
Теорема доказана.
Слайд 24
Доказательство Вальдхейма
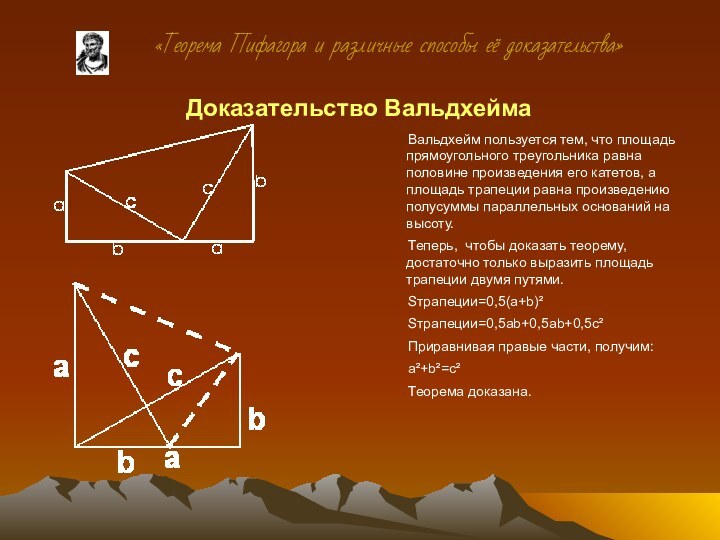
Вальдхейм пользуется тем, что площадь прямоугольного треугольника
равна половине произведения его катетов, а площадь трапеции равна
произведению полусуммы параллельных оснований на высоту.
Теперь, чтобы доказать теорему, достаточно только выразить площадь трапеции двумя путями.
Sтрапеции=0,5(a+b)²
Sтрапеции=0,5ab+0,5ab+0,5c²
Приравнивая правые части, получим:
a²+b²=c²
Теорема доказана.
Слайд 25
Доказательство основанное на теории подобия
В прямоугольном треугольника АВС
проведём из вершины прямого угла высоту CD; тогда треугольник
разобьётся на два треугольника, также являющихся прямоугольными.
Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия прямоугольных треугольников (по острому углу).
Из пропорциональности сторон подобных треугольников следуют верные равенства:
АC*AC=AB*AD; BC*BC=AB*BD;
Складывая эти два верных равенства, и получим, что c²=a²+b². Теорема доказана.
И тут я подумала: а ведь на занятиях математического кружка мы изучали и другие задачи по теории подобия. Нельзя ли их применить к доказательству теоремы Пифагора?
И получилось!
Давайте вместе с вами прочитаем одну маленькую геометрическую сказку.
Слайд 26
Маленькая – маленькая сказка,
где автор проекта приводит свои

доказательства
теоремы Пифагора
Жил-был на свете Прямоугольный Треугольник АВС. Жил, ни о чём не печалился. И вдруг однажды узнаёт, что в его владениях назревает большой скандал, о котором, не дай Бог, узнает всё человечество.
Дело в том, что две его стороны катеты a и b решили, что они вместе главнее Гипотенузы: ведь сумма их длин больше длины Гипотенузы, так , тем более, сумма квадратов катетов больше квадрата длины Гипотенузы!
«Тут и доказывать нечего!» - высокомерно твердили братья.
Гипотенуза с была спокойная, уравновешенная и поэтому очень огорчилась тем, что происходит в душах её братьев Катетов а и b. Она всегда их связывала и была опорой для их дома - Прямоугольного Треугольника АВС.
Надо доказать братьям, что она не только связывает их, но и площадь квадрата, построенного на гипотенузе, вовсе не меньше, а равна сумме площадей квадратов, построенных на катетах. «Но меня они не слушают! Пойду найду доброго человека, который бы доказал им это,»-решила Гипотенуза. А далеко идти и не пришлось. Совсем рядом - лицей №1571, а в нём учится Курманова Света, которая давно занимается этой проблемой.
Слайд 27
Проведём окружность с центром в точке А
и радиусом с.
В
М
N
D
A
C
а
с
b
В теории подобия доказывалось, что если две хорды окружности МN и ВD пересекаются в точке С, то
Теорема доказана.
ВС ∙ СD = МС ∙ СN
а∙а =(с - b) (с+b)
а2 = с2 - b2
с2 = а2 + b2
Слайд 28
ВС2 = ВМ⋅ВN
а2 = (с + b)(с–b)
а2 =
с2 - b2
с2 = а2 + b2
Из теории подобия известно, что если через точку В, лежащую вне окружности, провести касательную ВС (С – точка касания) и секущую, пересекающую окружность в точках М и N, то
В
С
А
М
N
а
с
b
Проведём окружность с центром в точке А и радиусом b.
Теорема доказана.