- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Треугольники
Содержание
- 2. ПланПонятие треугольника.Медианы, биссектрисы и высоты треугольника.Классификация треугольников.Первый
- 3. Понятие треугольникаА,В,С- вершины треугольникаАВ,ВС,АС- стороны треугольникаАВ+ВС+АС=Р, где Р – периметр треугольникаАСВ
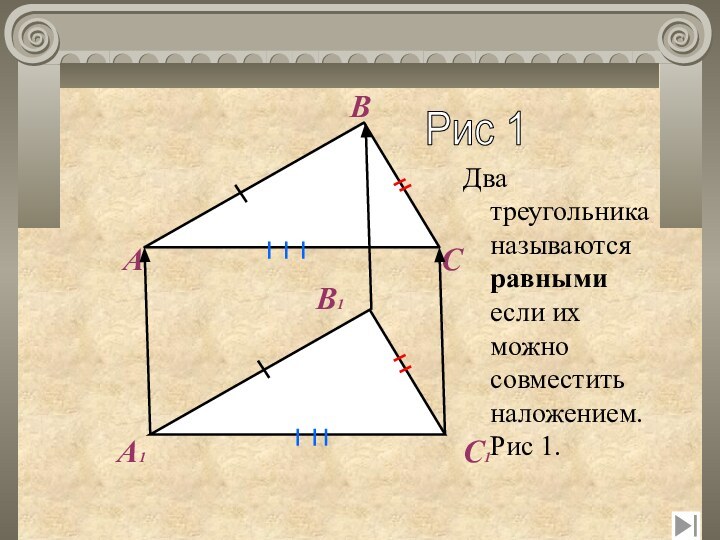
- 4. АА1В1ВСС1Рис 1Два треугольника называются равными если их можно совместить наложением. Рис 1.
- 5. Каждый из треугольников можно наложить на другой
- 6. Медиана Отрезок, соединяющий вершину треугольника с серединой
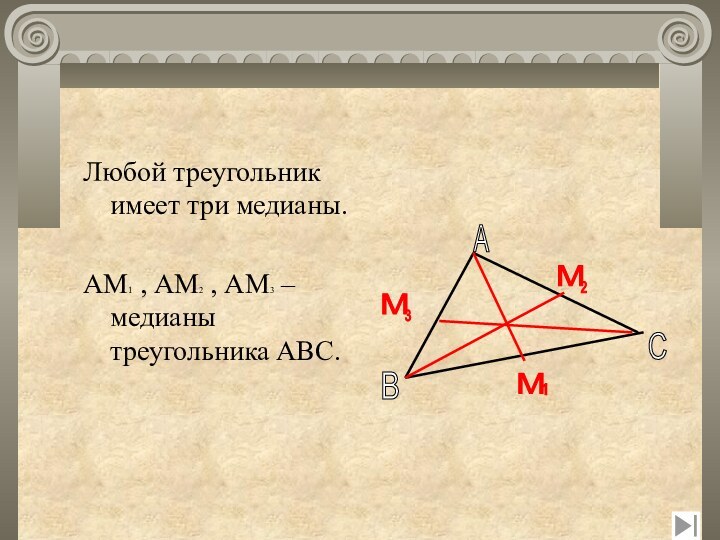
- 7. Любой треугольник имеет три медианы.АМ1 , АМ2 , АМ3 –медианы треугольника АВС.ABCМ 2М М 13
- 8. БиссектрисаОтрезок биссектрисы угла треугольника, соединяющий вершину треугольника
- 9. Любой треугольник имеет три биссектрисы. CC1, DD1 и EE1- биссектрисы треугольника CDE.DECCED111
- 10. Перпендикуляр, проведенный из вершины треугольника к
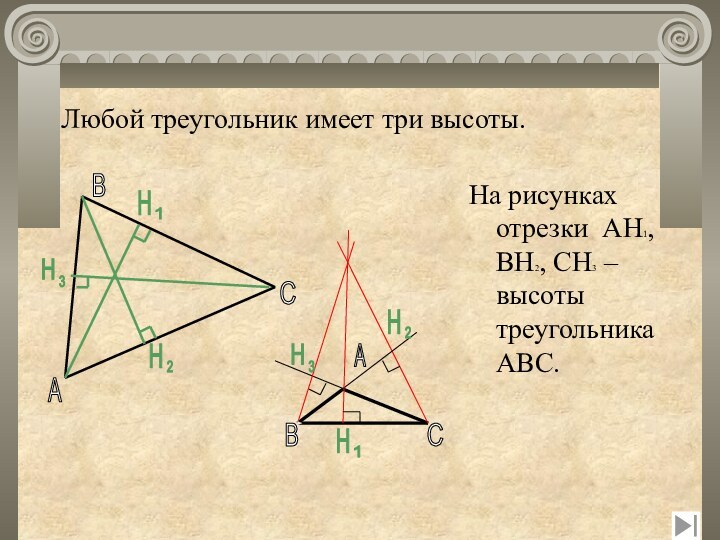
- 11. Любой треугольник имеет три высоты. ABCHHHНа рисунках отрезки AH1, BH2, CH3 – высоты треугольника ABC. ABC321H32HH1
- 12. Медианы, биссектрисы и высоты треугольника обладают замечательными
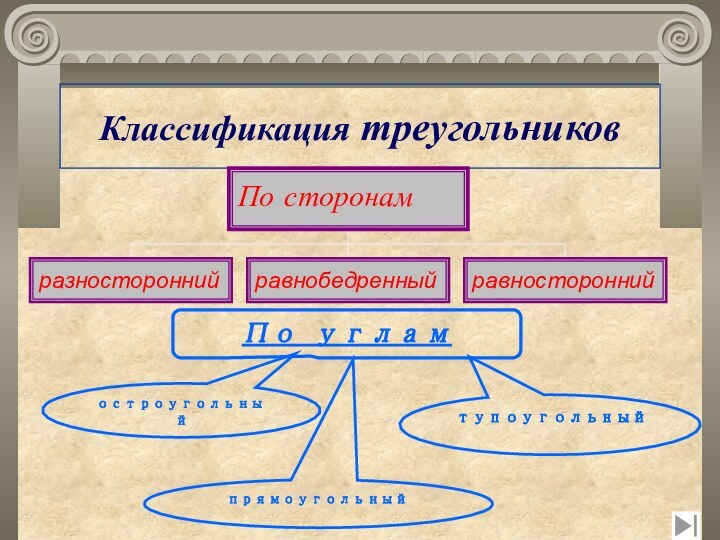
- 13. Классификация треугольниковПо угламтупоугольныйостроугольныйпрямоугольный
- 14. РазностороннийТреугольник называется разносторонним, если он имеет разные
- 15. РавнобедренныйТреугольник называется равнобедренным, если две его стороны
- 16. ТеоремаВ равнобедренном треугольнике углы при основании равны.1234ACDB
- 17. Рассмотрим равнобедренный треугольник ABC с основанием BC
- 18. РавностороннийABCТреугольник, все стороны которого равны, называется равносторонним или правильным AB=BC=CAA≠ B ≠ C
- 19. Первый признак равенства треугольниковТЕОРЕМАЕсли две стороны и
- 20. Первый признак равенства треугольниковДано: Δ АВС ,Δ
- 21. ДоказательствоТак как A= A1, то треугольник
- 22. Второй признак равенства треугольниковТЕОРЕМАЕсли сторона и два
- 23. Второй признак равенства треугольниковДано: Δ АВС ,Δ
- 24. ДоказательствоНаложим треугольник ABC на A 1B1C 1
- 25. Третий признак равенства треугольниковТЕОРЕМАЕсли три стороны одного
- 26. Третий признак равенства треугольниковДано: Δ АВС ,Δ
- 27. ДоказательствоПриложим треугольник ABC к треугольнику
- 28. Тест. 1.Для доказательства равенства треугольников АВС и
- 29. 5.В треугольнике АВС все стороны равны, и
- 30. Скачать презентацию
- 31. Похожие презентации
ПланПонятие треугольника.Медианы, биссектрисы и высоты треугольника.Классификация треугольников.Первый признак равенства треугольников.Второй признак равенства треугольников.Третий признак равенства треугольников.Тест .


















Слайд 2
План
Понятие треугольника.
Медианы, биссектрисы и высоты треугольника.
Классификация треугольников.
Первый признак
равенства треугольников.
Слайд 3
Понятие треугольника
А,В,С- вершины треугольника
АВ,ВС,АС- стороны треугольника
АВ+ВС+АС=Р, где
Р
– периметр треугольника
А
С
В
Слайд 4
А
А1
В1
В
С
С1
Рис 1
Два треугольника называются равными если их можно
совместить наложением. Рис 1.
Слайд 5 Каждый из треугольников можно наложить на другой так,
что они полностью совместятся, т.е попарно совместятся их вершины
и стороны. Таким образом, если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Слайд 6
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны,
называется медианой треугольника.
АМ-медиана треугольника АВС.
A
M
B
C
Слайд 8
Биссектриса
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны,
называется биссектрисой угла треугольника.
АА1- биссектриса
А треугольника АВС.A
B
C
A
1
Слайд 9
Любой треугольник имеет три биссектрисы.
CC1,
DD1 и EE1- биссектрисы треугольника CDE.
D
E
C
C
E
D
1
1
1
Слайд 10
Перпендикуляр, проведенный из вершины треугольника
к прямой,
называется высотой треугольника.
АН-высота треугольника АВС
H
A
B
C
Высота
Слайд 11
Любой треугольник имеет три высоты.
A
B
C
H
H
H
На рисунках отрезки
AH1, BH2, CH3 – высоты треугольника ABC.
A
B
C
3
2
1
H
3
2
H
H
1
Слайд 12
Медианы, биссектрисы и высоты треугольника обладают замечательными свойствами:
в
любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются
в одной точке; высоты или их продолжения также пересекаются в одной точке
Слайд 14
Разносторонний
Треугольник называется разносторонним, если он имеет разные стороны
и углы.
A
B
C
A≠ B ≠ C
AB=BC=CA
Слайд 15
Равнобедренный
Треугольник называется равнобедренным,
если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона –
основанием равнобедренного треугольника.
Основание
Боковая
сторона
Боковая
сторона
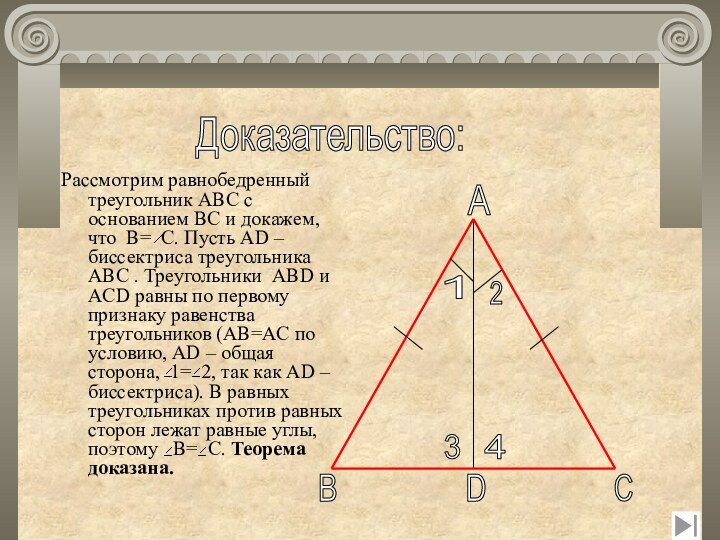
Слайд 17 Рассмотрим равнобедренный треугольник ABC с основанием BC и
докажем, что B= C. Пусть AD – биссектриса треугольника
ABC . Треугольники ABD и ACD равны по первому признаку равенства треугольников (AB=AC по условию, AD – общая сторона, 1= 2, так как AD –биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому B= C. Теорема доказана.Доказательство:
1
2
3
4
A
C
D
B
Слайд 18
Равносторонний
A
B
C
Треугольник, все стороны которого равны, называется равносторонним или
правильным
AB=BC=CA
A≠ B ≠ C
Слайд 19
Первый признак равенства треугольников
ТЕОРЕМА
Если две стороны и угол
между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие треугольники равны.
Слайд 20
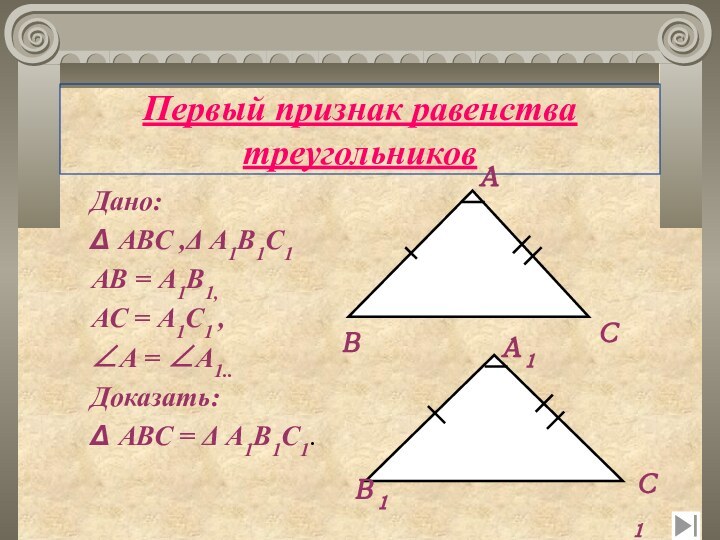
Первый признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
АВ
= А1В1,
АС = А1С1 ,
А = А1..
Доказать:
Δ АВС =
Δ А1В1С1.
А
В
С
А1
В1
С1
Слайд 21
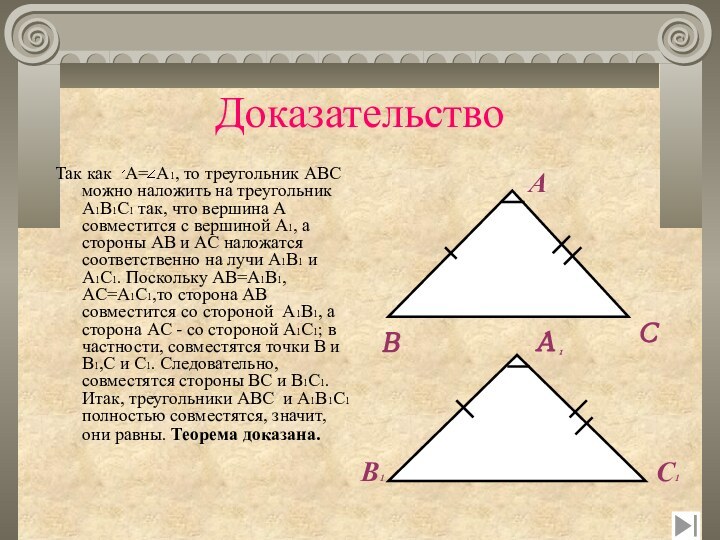
Доказательство
Так как A= A1, то треугольник ABC
можно наложить на треугольник A1B1C1 так, что вершина A
совместится с вершиной A1, а стороны AB и AC наложатся соответственно на лучи A1B1 и A1C1. Поскольку AB=A1B1, AC=A1C1,то сторона AB совместится со стороной A1B1, а сторона AC - со стороной A1C1; в частности, совместятся точки B и B1,C и C1. Следовательно, совместятся стороны BC и B1C1. Итак, треугольники ABC и A1B1C1 полностью совместятся, значит, они равны. Теорема доказана.
В
С
А1
А
В1
С1
Слайд 22
Второй признак равенства треугольников
ТЕОРЕМА
Если сторона и два прилежащих
к ней угла одного треугольника соответственно равны стороне и
двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Слайд 23
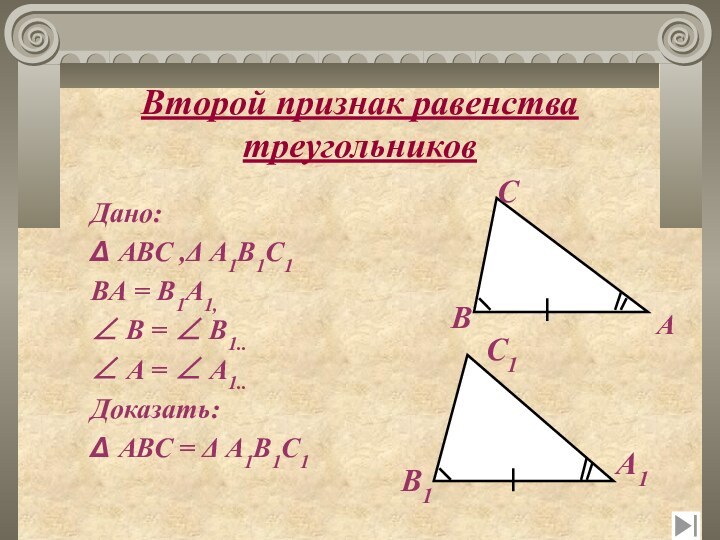
Второй признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
ВА
= В1А1,
В = В1..
А =
А1..Доказать:
Δ АВС = Δ А1В1С1
А1
В
А
В1
С
С1
Слайд 24
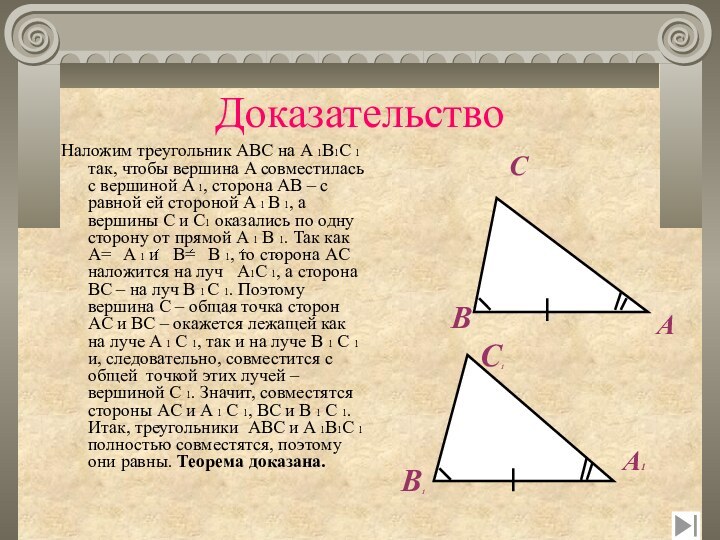
Доказательство
Наложим треугольник ABC на A 1B1C 1 так,
чтобы вершина A совместилась с вершиной A 1, сторона
AB – c равной ей стороной A 1 B 1, а вершины C и C1 оказались по одну сторону от прямой A 1 B 1. Так как A= A 1 и B= B 1, то сторона AC наложится на луч A1C 1, а сторона BC – на луч B 1 C 1. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче A 1 C 1, так и на луче B 1 C 1 и, следовательно, совместится с общей точкой этих лучей – вершиной C 1. Значит, совместятся стороны AC и A 1 C 1, BC и B 1 C 1. Итак, треугольники ABC и A 1B1C 1 полностью совместятся, поэтому они равны. Теорема доказана.
В
А
В1
С1
С
А1
Слайд 25
Третий признак равенства треугольников
ТЕОРЕМА
Если три стороны одного треугольника
соответственно равны трем сторонам другого треугольника, то такие треугольники
равны.
Слайд 26
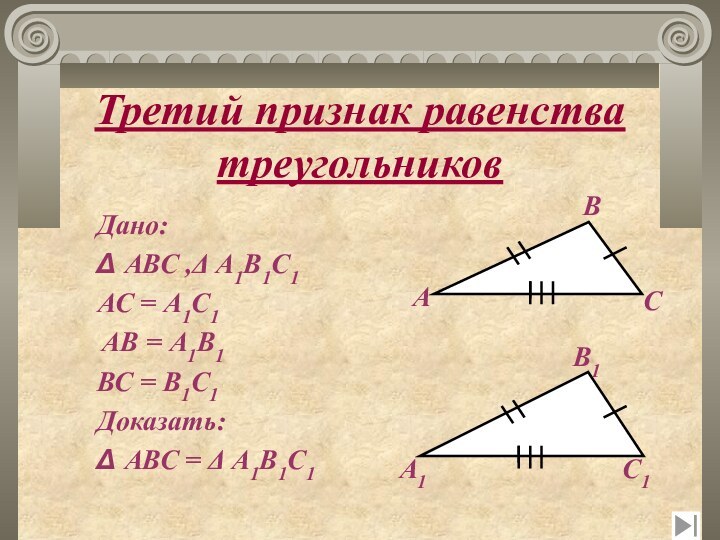
Третий признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
АС
= А1С1
АВ = А1В1
ВС = В1С1
Доказать:
Δ АВС =
Δ А1В1С1А
В
С
А1
В1
С1
Слайд 27
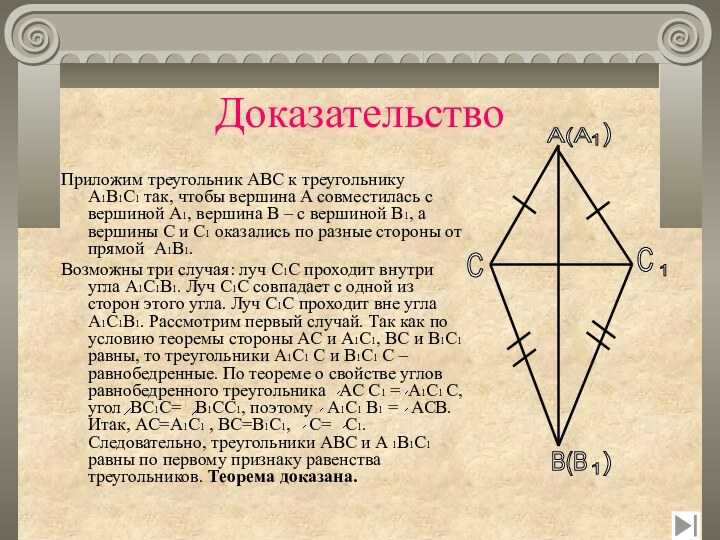
Доказательство
Приложим треугольник ABC к треугольнику
A1B1C1 так, чтобы вершина A совместилась с вершиной
A1, вершина B – с вершиной B1, а вершины C и C1 оказались по разные стороны от прямой A1B1.Возможны три случая: луч C1C проходит внутри угла A1C1B1. Луч C1C совпадает с одной из сторон этого угла. Луч C1C проходит вне угла A1C1B1. Рассмотрим первый случай. Так как по условию теоремы стороны AC и A1C1, BC и B1C1 равны, то треугольники A1C1 C и B1C1 C – равнобедренные. По теореме о свойстве углов равнобедренного треугольника AС C1 = A1C1 С, угол BС1С= B1СС1, поэтому A1C1 B1 = ACB. Итак, AC=A1C1 , BC=B1C1, C= C1. Следовательно, треугольники ABC и A 1B1C1 равны по первому признаку равенства треугольников. Теорема доказана.
A(A
1
)
C
C
1
В(В
1
)
Слайд 28
Тест.
1.Для доказательства равенства треугольников
АВС и DEF(рис1)
достаточно знать, что:
а) АВ=DF; б)АС=DE; в)АВ=DE.
2.Для доказательства равенства треугольников
АВС и EDF(рис 2) достаточно доказать, что:а) А= D б) В= D в) А= Е .
3.Из равенства треугольников АВС и FDE(рис 3)следует, что:
а)АВ=FD б)АС=DF в)АВ=EF .
4.Из равенства треугольников АВС и DEF(рис 4) следует, что:
а) В= D б) А= Е в) С= F .
A
B
C
D
E
F
B
C
A
E
E
E
D
D
D
F
F
F
A
A
B
B
C
C
рис.1
рис.2
рис.4
рис.3
Слайд 29 5.В треугольнике АВС все стороны равны, и в
треугольнике DEF все стороны равны. Чтобы доказать равенство треугольников
АВС и DEF достаточно доказать, что :а) В= D; б)АВ=DE; в)РАВС=РDEF .
6. «Медиана в равнобедренном треугольнике является биссектрисой и высотой».Это утверждение :
а)верно всегда; б)всегда неверно; в)может быть верно.
7.В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а)в любом; б)в равнобедренном; в)в равностороннем.
8.Если в треугольнике два угла равны, то этот треугольник:
а)равнобедренный; б)равносторонний; в)прямоугольный.
9.Если треугольник равносторонний, то:
а)он равнобедренный; б)все его углы равны;
в) любая его биссектриса является медианой и высотой.