- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Треугольник Пифагора
Содержание
- 2. Пифагор (др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras;
- 3. В современном мире Пифагор считается великим математиком
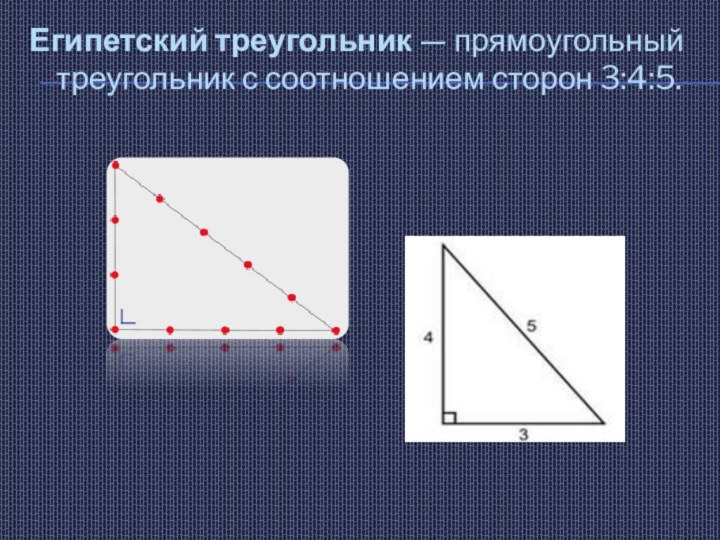
- 4. Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
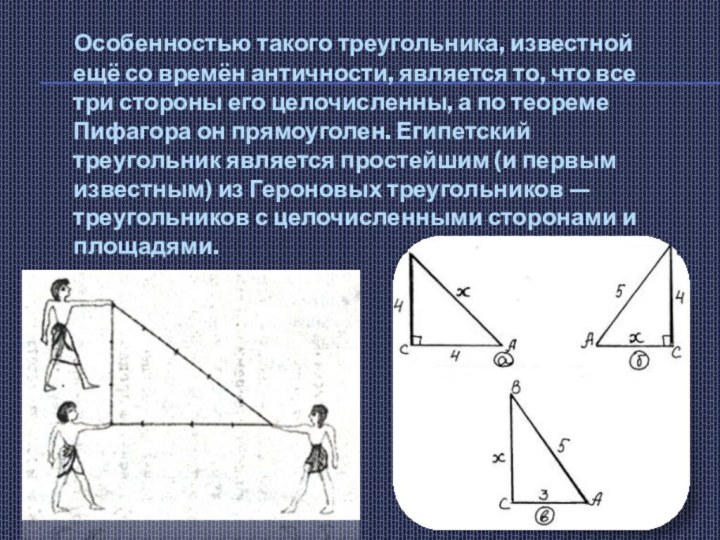
- 5. Особенностью такого треугольника, известной ещё
- 6. Название треугольнику с таким отношением сторон дали
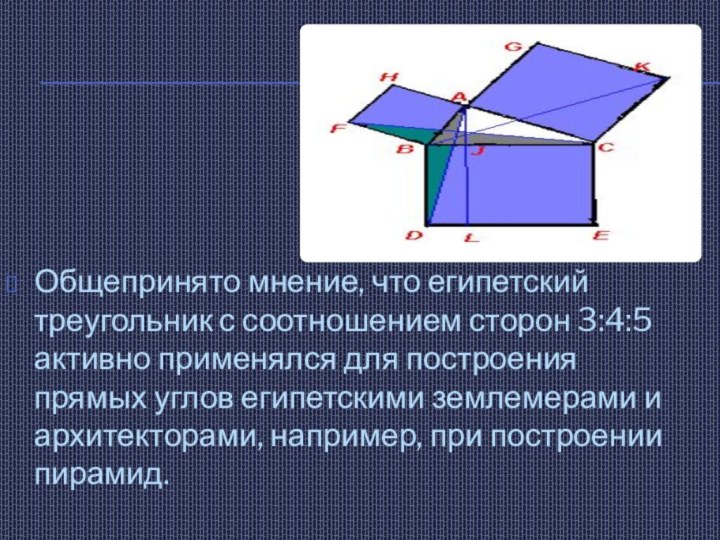
- 7. Общепринято мнение, что египетский треугольник с соотношением
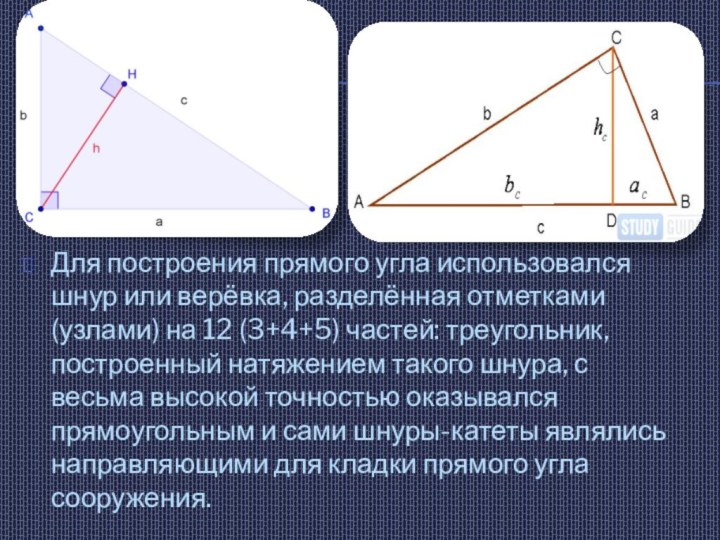
- 8. Для построения прямого угла использовался шнур или
- 9. Скачать презентацию
- 10. Похожие презентации
Пифагор (др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570—490 гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.