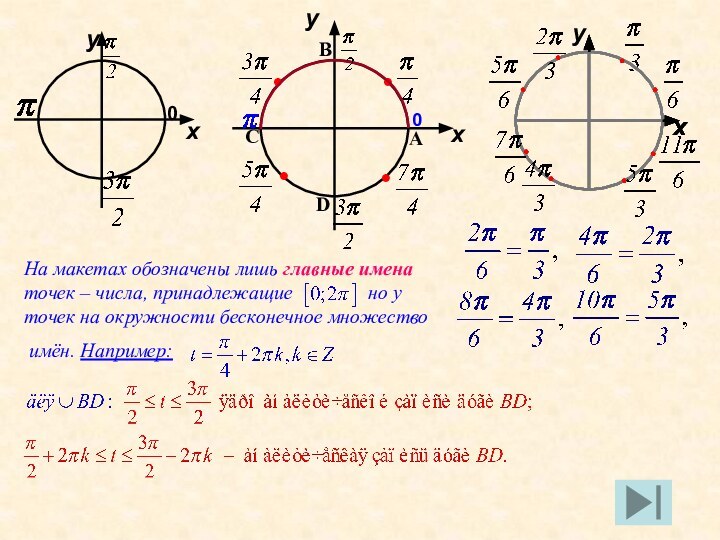
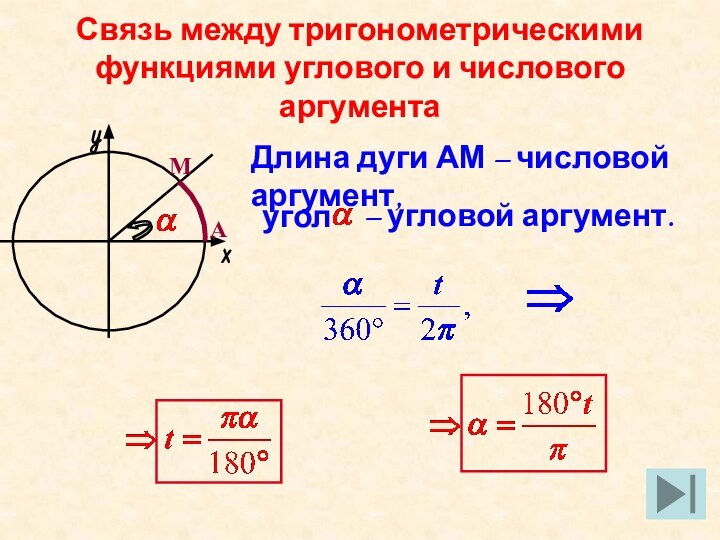
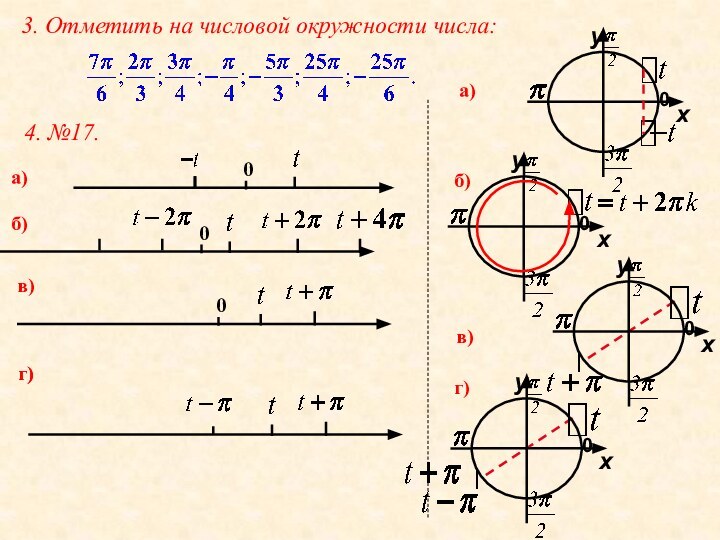
числа, принадлежащие
но у точек на окружности бесконечное множествоимён. Например:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





+
–
–
+
•
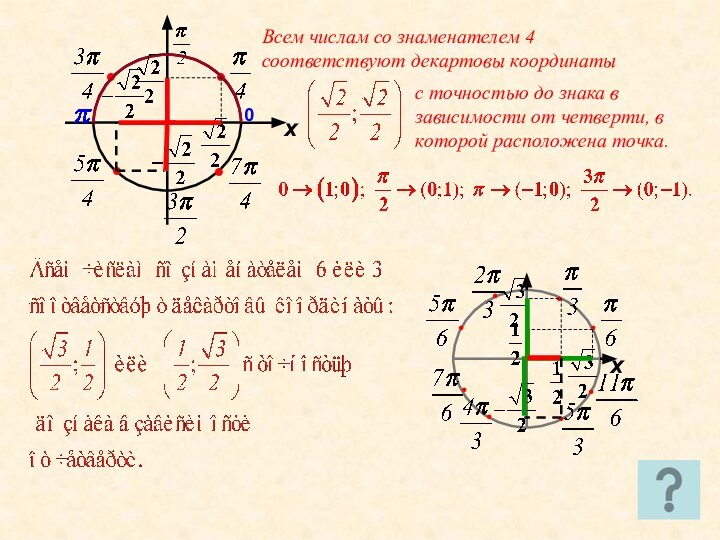
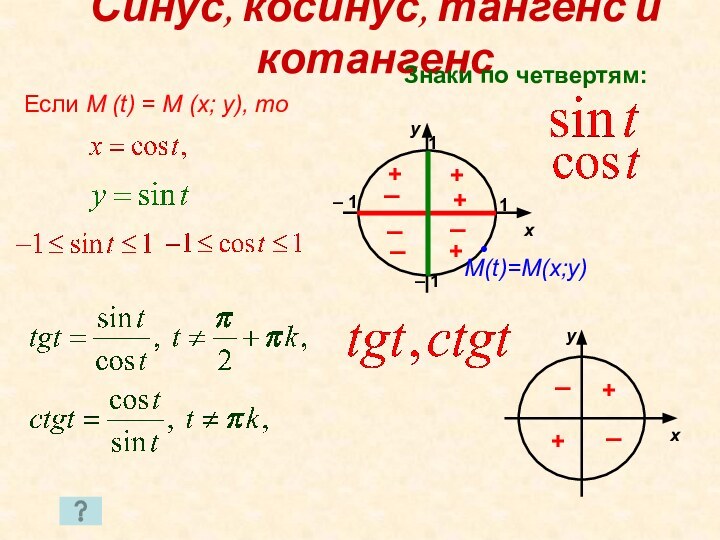
M(t)=M(x;y)
– 1
1
– 1
1
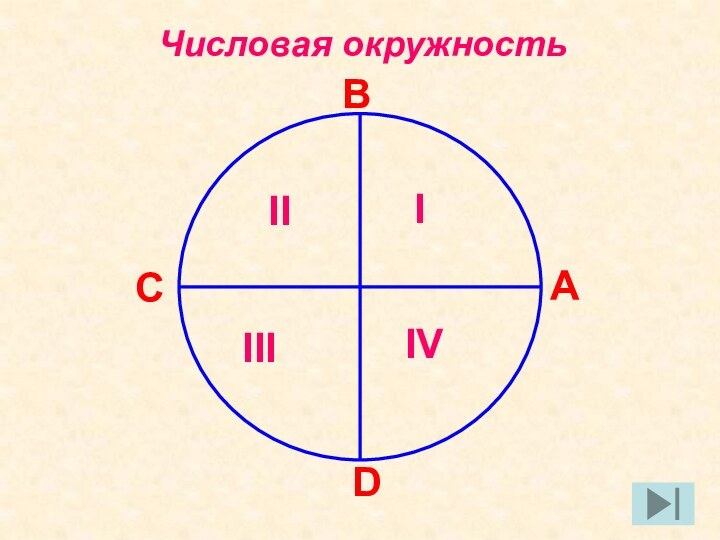
Знаки по четвертям:
+
–
+
–
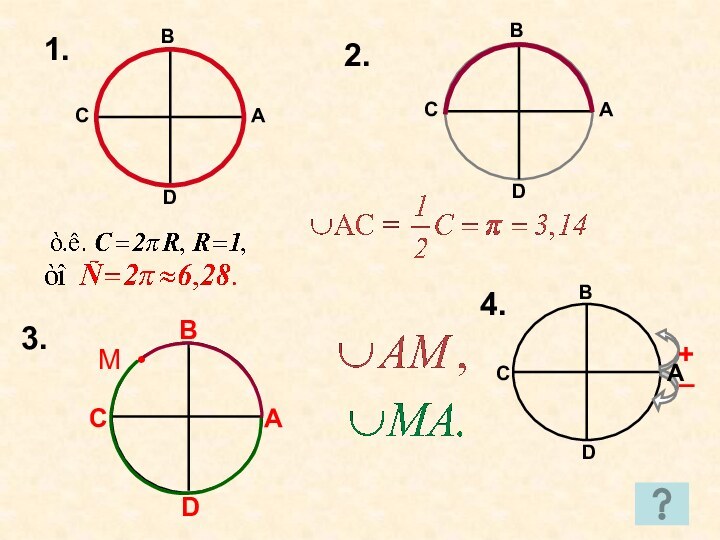
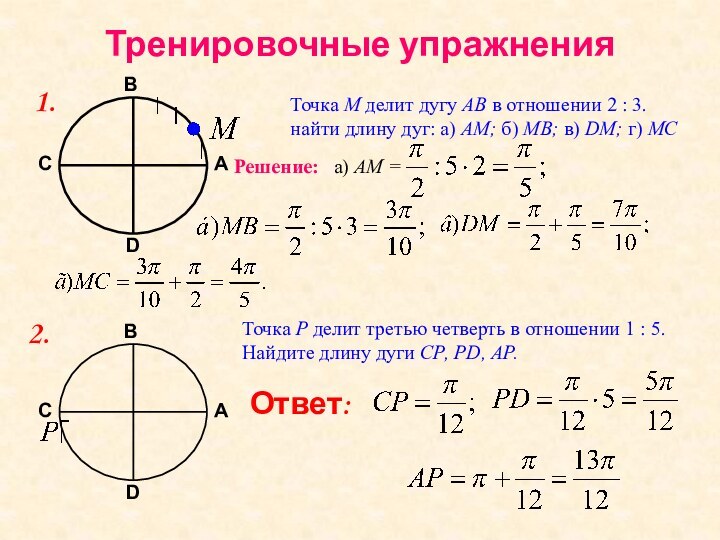
Решение: а) АМ =
2.
Точка Р делит третью четверть в отношении 1 : 5. Найдите длину дуги СР, РD, АР.
Ответ: