— неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия
тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.Отсутствие или нарушение симметрии называется асимметрией.
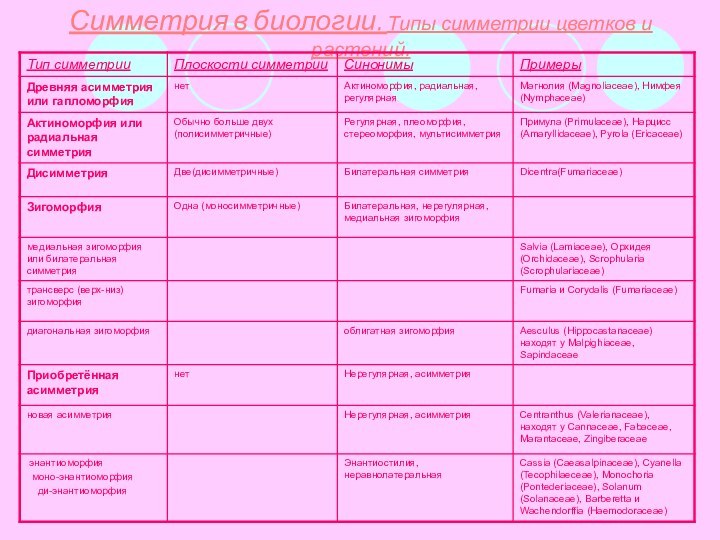
Виды симметрий.
Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией.
Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:
Отражательная симметрия. В математике (точнее, евклидовой геометрии) осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.
Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
Иногда вводят также (осевую) симметрию некоторого порядка:
Осевая симметрия n-го порядка - симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Zn.
Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка.