Слайд 2
Essential Math for Games
Collisions
Up to this point, objects
just pass through each other
Two parts to handling collisions
Collision
detection – uses computational geometry techniques (useful in other ways, too)
Collision response – modifying physical simulation
Слайд 3
Essential Math for Games
Computational Geometry
Algorithms for solving geometric
problems
Object intersections
Object proximity
Path planning
Слайд 4
Essential Math for Games
Distance Testing
Useful for computing intersection
between simple objects
E.g. sphere intersection boils down to point-point
distance test
Just cover a few examples
Слайд 5
Essential Math for Games
Point-Point Distance
Compute length of vector
between two points P0 and P1, or
Слайд 6
Essential Math for Games
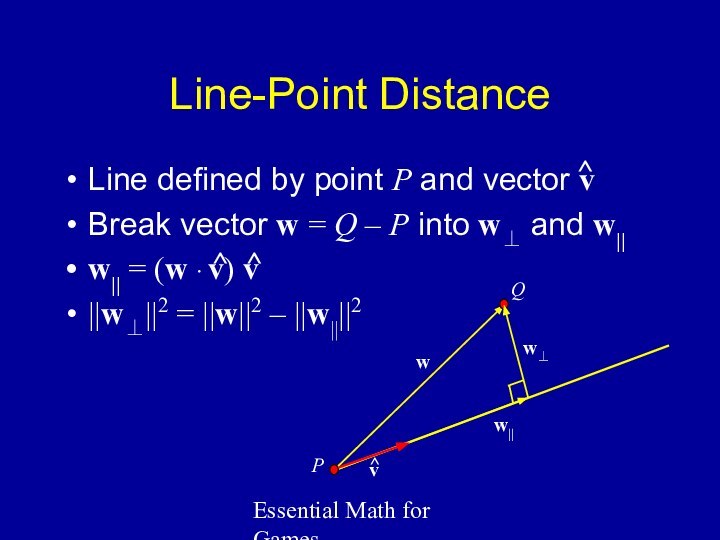
Line-Point Distance
Line defined by point
P and vector v
Break vector w = Q –
P into w⊥ and w||
w|| = (w ∙ v) v
||w⊥||2 = ||w||2 – ||w||||2
^
^
^
v
Q
P
w
w||
w⊥
^
Слайд 7
Essential Math for Games
Line-Point Distance
Final formula:
If v isn't
normalized:
Слайд 8
Essential Math for Games
Line-Line Distance
From http://www.geometryalgorithms.com
Vector wc perpendicular
to u and v or
Two equations
Two unknowns
P0
u
Q0
v
P(sc)
Q(tc)
wc
Слайд 9
Essential Math for Games
Line-Line Distance
Final equations:
P0
u
Q0
v
P(sc)
Q(tc)
Слайд 10
Essential Math for Games
Segment-Segment Distance
Determine closest point between
lines
If lies on both segments, done
Otherwise clamp against nearest
endpoint and recompute
See references for details
Слайд 11
Essential Math for Games
Bounding Objects
Detecting intersections with complex
objects expensive
Provide simple object that surrounds them to cheaply
cull out obvious cases
Use for collision, rendering, picking
Cover in increasing order of complexity
Слайд 12
Essential Math for Games
Bounding Sphere
Tightest sphere that surrounds
model
For each point, compute distance from center, save max
for radius
Слайд 13
Essential Math for Games
Bounding Sphere (Cont’d)
What to use
for center?
Local origin of model
Centroid (average of all points)
Center
of bounding box
Want a good fit to cull as much as possible
Linear programming gives smallest fit
Слайд 14
Essential Math for Games
Sphere-Sphere Collision
Compute distance d between
centers
If d < r1 + r2, colliding
Note: d2 is
not necessarily < r12 + r22
want d2 < (r1 + r2)2
d
r1
r2
Слайд 15
Essential Math for Games
Bounding Box
Tightest box that surrounds
model
Compare points to min/max vertices
If element less/greater, set element
in min/max
(min x, min y)
(max x, max y)
Слайд 16
Essential Math for Games
Axis-Aligned Bounding Box
Box edges aligned
to world axes
Recalc when object changes orientation
Collision checks are
cheaper though
Слайд 17
Essential Math for Games
Axis-Aligned Box-Box Collision
Compare x values
in min,max vertices
If min2 > max1 or min1 >
max2, no collision (separating plane)
Otherwise check y and z directions
min1
max1
min2
max2
Слайд 18
Essential Math for Games
Object-Oriented Bounding Box
Box edges aligned
with local object coordinate system
Much tighter, but collision calcs
costly
Слайд 19
Essential Math for Games
OBB Collision
Idea: determine if separating
plane between boxes exists
Project box extent onto plane vector,
test against projection btwn centers
c∙v
b∙v
a∙v
a
b
c
Слайд 20
Essential Math for Games
OBB Collision
To ensure maximum extents,
take dot product using only absolute values
Check against axes
for both boxes, plus cross products of all axes
See Gottschalk for more details
Слайд 21
Essential Math for Games
Capsule
Cylinder with hemispheres on ends
One
way to compute
Calc bounding box
Use long axis for length
Next
largest width for radius
Слайд 22
Essential Math for Games
Capsule
Compact
Only store radius, endpoints of
line segment
Oriented shape w/faster test than OBB
Test path collision
Слайд 23
Essential Math for Games
Capsule-Capsule Collision
Key: swept sphere axis
is line segment with surrounding radius
Compute distance between line
segments
If less than r1 + r2, collide
Слайд 24
Essential Math for Games
Caveat
Math assumes infinite precision
Floating point
is not to be trusted
Precision worse farther from 0
Use
epsilons
Careful of operation order
Re-use computed results
More on floating point on website
Слайд 25
Essential Math for Games
Which To Use?
As many as
necessary
Start with cheap tests, move up the list
Sphere
Swept Sphere
Box
May
not need them all
Слайд 26
Essential Math for Games
Recap
Sphere -- cheap, not a
good fit
AABB -- still cheap, but must recalc and
not a tight fit
Swept Sphere -- oriented, cheaper than OBB but generally not as good a fit
OBB -- somewhat costly, but a better fit
Слайд 27
Essential Math for Games
Collision Detection
Naïve: n2 checks!
Two part
process
Broad phase
Cull out non-colliding pairs
Narrow phase
Determine penetration and contact
points between pairs
Слайд 28
Essential Math for Games
Broad Phase
Obvious steps
Only check each
pair once
Flag object if collisions already checked
Only check moving
objects
Check against other moving and static
Check rough bounding object first
AABB or sphere
Слайд 29
Essential Math for Games
Hierarchical Systems
Can break model into
hierarchy and build bounds for each level of hierarchy
Finer
level of detection
Test top level, cull out lots of lower levels
Слайд 30
Essential Math for Games
Hierarchical Systems
Can use scene graph
to maintain bounding information
Propagate transforms down to children
Propagate bound
changes up to root
Слайд 31
Essential Math for Games
Spatial Subdivision
Break world into separate
areas
Only check your area and neighbors
Simplest: uniform
Slabs
Grid
Voxels
Слайд 32
Essential Math for Games
Sweep and Prune
Store sorted x
extents of objects
Sweep from min x to max x
As
object min value comes up, make active, test against active objects
Can extend to more dimensions
Слайд 33
Essential Math for Games
Spatial Subdivision
Other methods:
Quadtrees, octrees
BSP trees,
kd-trees
Room-portal
Choice depends on your game type, rendering engine, memory
available, etc.
Слайд 34
Essential Math for Games
Temporal Coherence
Objects nearby generally stay
nearby
Check those first
Can take memory to store information
Слайд 35
Essential Math for Games
Narrow Phase
Have culled object pairs
Need
to find
Contact point
Normal
Penetration (if any)
Слайд 36
Essential Math for Games
Contact Region
Two objects interpenetrate, have
one (or more) regions
A bit messy to deal with
Many
try to avoid interpenetration
Слайд 37
Essential Math for Games
Contact Features
Faceted objects collide at
pair of contact features
Only consider E-E and F-V pairs
Infinite
possibilities for normals for others
Can generally convert to E-E and F-V
Ex: V-V, pick neighboring face for one
Слайд 38
Essential Math for Games
Contact Features
For E-E:
Point is intersection
of edges
Normal is cross product of edge vectors
For F-V:
Point
is vertex location
Normal is face normal
Слайд 39
Essential Math for Games
Contact Points
Can have multiple contact
points
Ex: two concave objects
Store as part of collision detection
Collate as part of collision resolution
Слайд 40
Essential Math for Games
Example: Spheres
Difference between centers gives
normal n (after you normalize)
Penetration distance p is p =
(r1+r2) - ||c2-c1||
c1
c2
Слайд 41
Essential Math for Games
Example: Spheres
Collision point: average of
penetration distance along extended normal
If touching, where normal
crosses sphere
v = ½(c1 + r1n + c2 - r2n)
^
^
c1
c2
Слайд 42
Essential Math for Games
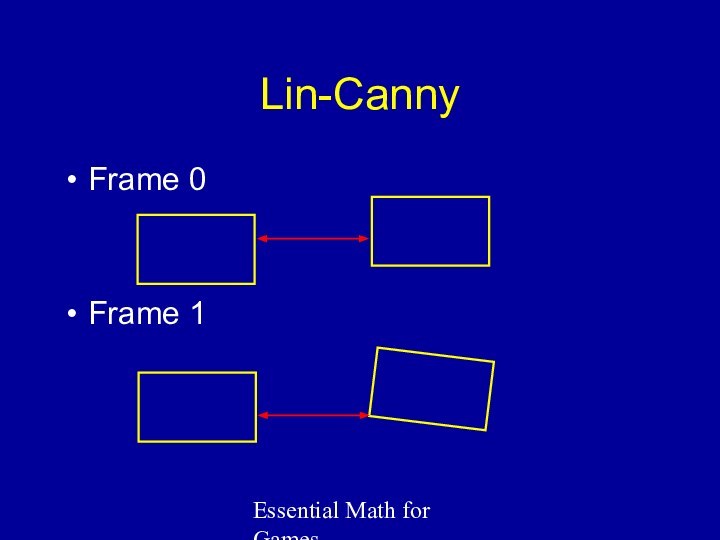
Lin-Canny
For convex objects
Easy to understand,
hard to implement
Closest features generally same from frame to
frame
Track between frames
Modify by walking along object
Слайд 43
Essential Math for Games
Lin-Canny
Frame 0
Frame 1
Слайд 44
Essential Math for Games
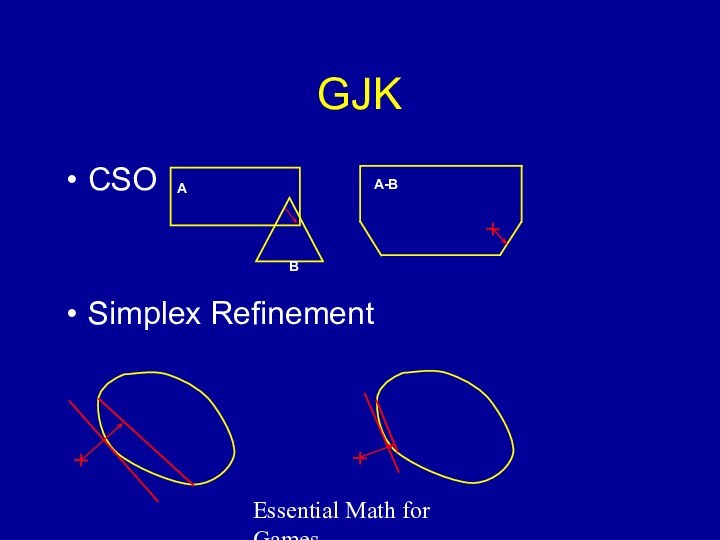
GJK
For Convex Objects
Hard to understand,
easy to implement
Finds point in Configuration Space Obstacle closest
to origin. Corresponds to contact point
Iteratively finds points by successive refinement of simplices
Слайд 45
Essential Math for Games
GJK
CSO
Simplex Refinement
Слайд 46
Essential Math for Games
Missing Collision
If time step is
too large for object speed, two objects may pass
right through each other without being detected (tunneling)
Слайд 47
Essential Math for Games
Missing Collision
One solution: slice time
interval
Simulate between slices
Same problem, just reduced frequency
Слайд 48
Essential Math for Games
Missing Collision
Another solution: use swept
volumes
If volumes collide, may collide in frame
With more work
can determine time-of-impact (TOI), if any
Слайд 49
Essential Math for Games
Recap
Collision detection complex
Combo of math
and computing
Break into two phases: broad and narrow
Be careful
of tunneling
Слайд 50
Essential Math for Games
References
Preparata, Franco P. and Michael
Ian Shamos, Computational Geometry: An Introduction, Springer-Verlag, New York,
1985.
O’Rourke, Joseph, Computational Geometry in C, Cambridge University Press, New York, 1994.
Eberly, David H., 3D Game Engine Design, Morgan Kaufmann, San Francisco, 2001.
Gottschalk, Stephan, Ming Lin and Dinesh Manocha, “OBB-Tree: A Hierarchical Structure for Rapid Interference Detection,” SIGGRAPH ‘96.