- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Удивительный мир симметрии
Содержание
- 3. Герман Вейль"Симметрия, как бы широко или узко
- 4. В.И. Вернадский“Симметрия устанавливает забавное и удивительное родство
- 5. АристотельМатематика выявляет порядок, симметрию и определенность, а это - важнейшие виды прекрасного.
- 6. Виды геометрических симметрий Основные виды:Зеркальная симметрияОсевая симметрияВращательная
- 7. Зеркальная симметрия Зеркальная симметрия — это тип
- 8. Осевая симметрия Фигура называется симметричной относительно прямой
- 9. Вращательная симметрия Вращательная симметрия- термин, означающий симметрию
- 10. Центральная симметрия Центральная симметрия - фигура называется
- 11. Винтовая симметрия Винтовая симметрия - это симметрия
- 12. Симметрии в физикеСимметрия - одно из фундаментальных
- 13. Симметрии в биологииСимметрия в биологии проявляется в
- 14. Симметрия в биологииВ XX веке усилиями российских
- 15. Симметрия в биологии
- 16. Симметрия в биологии
- 17. Симметрия в биологии
- 18. Симметрия в химииСимметрия в химии проявляется в
- 19. Симметрия в химии
- 20. Симметрия в химии
- 21. Симметрия в архитектуреЛе Корбюзье, в своей книге
- 22. Симметрия в архитектуре
- 23. Симметрия в архитектуре
- 24. Симметрия в архитектуре
- 25. Симметрия в религииПредполагается, что тенденция людей видеть
- 26. Симметрия в религии
- 27. Симметрия в религии
- 28. Симметрия в живописи
- 29. Симметрия в живописи
- 30. Симметрия в живописи
- 31. Симметрия в живописи
- 32. Симметрия в музыкеПонятие симметрии в музыке появилось
- 33. Виды симметрии в музыкеРакоходное отражениеОбращение интервалаРакоходное обращениеТрансляционный видСеквенцияРакоходное обращении с зеркальным отражением
- 34. Ракоходное отражениеВ этом случае зеркальная плоскость ориентирована
- 35. Обращение интервалаЭто самый редковстречающийся вид. Обращение исходит
- 36. Ракоходное обращениеПри этом в зеркальной части снова
- 37. Трансляционный видЭто самый распространенный вид симметрии в
- 38. СеквенцияРазновидность трансляции. Многократное повторение небольшого мотива разных
- 39. Ракоходное обращении с зеркальным отражениемПри этом нотный
- 40. Симметрия в жизни человека
- 41. Скачать презентацию
- 42. Похожие презентации
СимметрияСимметрия (от греч. symmetria - соразмерность) - свойство форм предмета иметь части, повторяющиеся при повороте на определенный угол вокруг своей оси и, отражения его в плоскости или точке.




































Слайд 2
Симметрия
предмета иметь части, повторяющиеся при повороте на определенный угол вокруг своей оси и, отражения его в плоскости или точке.
Слайд 3
Герман Вейль
"Симметрия, как бы широко или узко мы
не понимали это слово, есть идея, с помощью которой
человек пытался объяснить и создать порядок, красоту и совершенство".
Слайд 4
В.И. Вернадский
“Симметрия устанавливает забавное и удивительное родство между
предметами, явлениями и теориями, внешне никак не связанными: земным
магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, скарабеями, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности.Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности”
Слайд 5
Аристотель
Математика выявляет порядок, симметрию и определенность, а
это - важнейшие виды прекрасного.
Слайд 6
Виды геометрических симметрий
Основные виды:
Зеркальная симметрия
Осевая симметрия
Вращательная симметрия
Центральная
симметрия
Винтовая симметрия
Так же есть другие виды:
Фрактальные симметрии
Неизометричная симметрия
Поступательная симметрия
Точечная
симметрияСкользящая симметрия
Но к ним нужен более детальный подход
Слайд 7
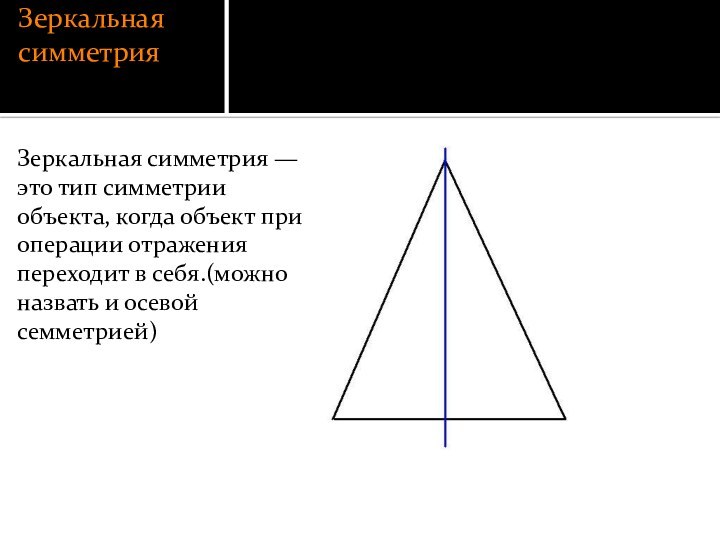
Зеркальная симметрия
Зеркальная симметрия — это тип симметрии объекта,
когда объект при операции отражения переходит в себя.(можно назвать
и осевой семметрией)
Слайд 8
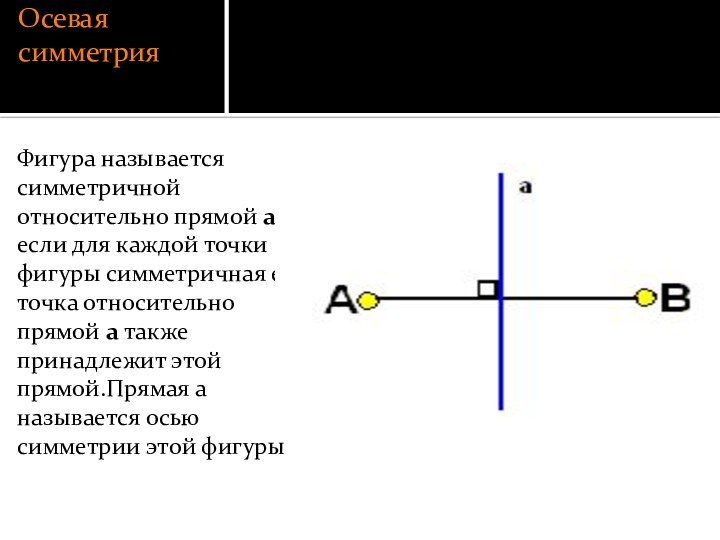
Осевая симметрия
Фигура называется симметричной относительно прямой a, если
для каждой точки фигуры симметричная ей точка относительно прямой
a также принадлежит этой прямой.Прямая a называется осью симметрии этой фигуры
Слайд 9
Вращательная симметрия
Вращательная симметрия- термин, означающий симметрию объекта относительно
всех или некоторых собственных вращений m-мерного евклидова пространства.
Слайд 10
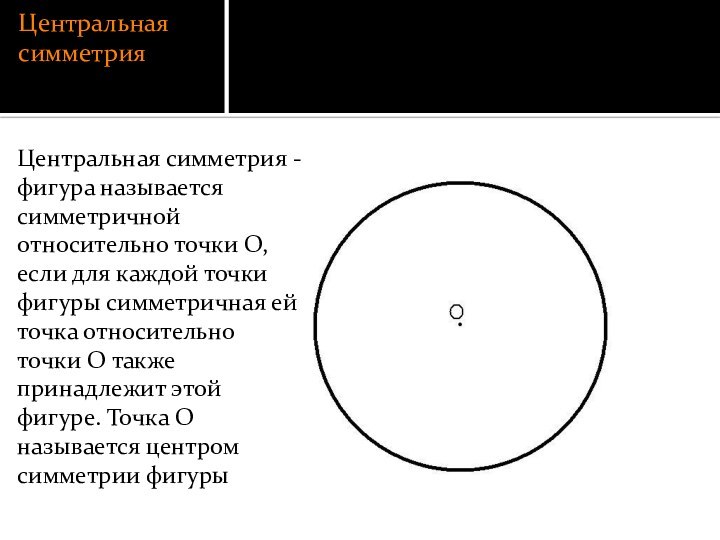
Центральная симметрия
Центральная симметрия - фигура называется симметричной относительно
точки О, если для каждой точки фигуры симметричная ей
точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры
Слайд 11
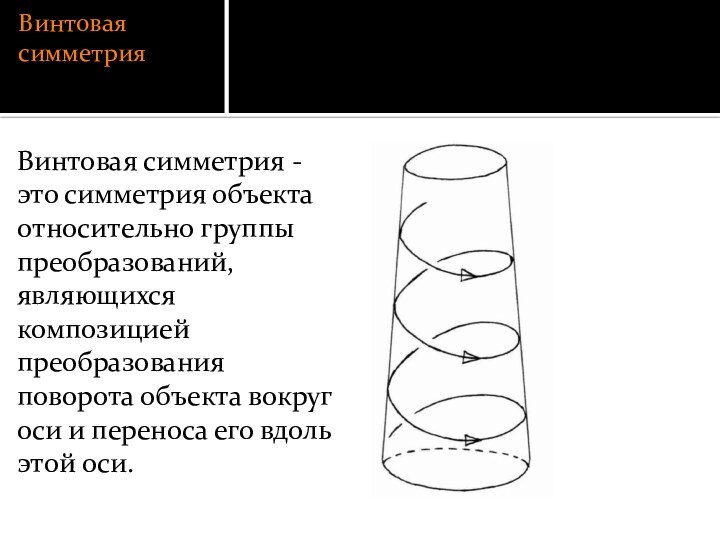
Винтовая симметрия
Винтовая симметрия - это симметрия объекта относительно
группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси
и переноса его вдоль этой оси.
Слайд 12
Симметрии в физике
Симметрия - одно из фундаментальных понятий
в современной физике, играющее важнейшую роль в формулировке современных
физических теорий. Симметрии, учитываемые в физике, довольно разнообразны, начиная с симметрий обычного трёхмерного «физического пространства» (такими, например, как зеркальная симметрия), продолжая более абстрактными и менее наглядными (такими как калибровочная инвариантность).Принципы симметрии являются в физике инструментом для отыскания новых законов природы. К числу симметричных принципов относится принцип относительности Галилея и Эйнштейна
Слайд 13
Симметрии в биологии
Симметрия в биологии проявляется в закономерном
расположении подобных (одинаковых) частей тела или форм живого организма,
совокупности живых организмов относительно центра или оси симметрии.
Слайд 14
Симметрия в биологии
В XX веке усилиями российских учёных
- В Беклемишева, В Вернадского, В Алпатова, Г.Гаузе -
было создано новое направление в учении о симметрии - биосимметрика
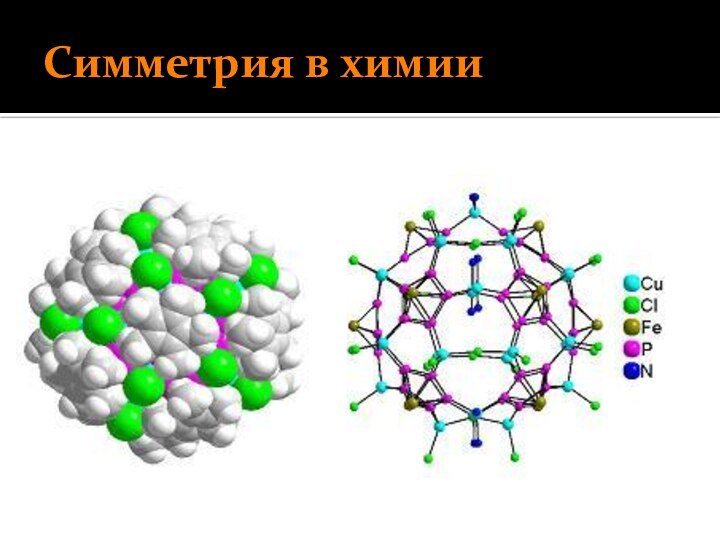
Слайд 18
Симметрия в химии
Симметрия в химии проявляется в геометрической
конфигурации молекул, что сказывается на специфике физических и химических
свойств молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами.
Слайд 21
Симметрия в архитектуре
Ле Корбюзье, в своей книге «Архитектура
XX века» писал: «Человеку необходим порядок: без него все
его действия теряют согласованность, логическую взаимность. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядок, который продиктован ему потребностями его психики, это творческий процесс. Творчество есть акт упорядочения».
Слайд 25
Симметрия в религии
Предполагается, что тенденция людей видеть цель
в симметрии, является одной из причин, почему симметрия часто
является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.
Слайд 32
Симметрия в музыке
Понятие симметрии в музыке появилось благодаря
музыкальному деятелю Э.К. Розенову. Во второй половине 19 века
анализируя произведения Баха он пришёл к выводу, что в них «господствуют закон золотого сечения и закон симметрии .»« Мы с тем большим правом можем приложить к музыкальному произведению понятие симметрии, что это произведение записывается при помощи нот, т. е. получает пространственный геометрический образ, части которого мы можем обозревать.» Г.В.Вульф
Слайд 33
Виды симметрии в музыке
Ракоходное отражение
Обращение интервала
Ракоходное обращение
Трансляционный вид
Секвенция
Ракоходное
обращении с зеркальным отражением
Слайд 34
Ракоходное отражение
В этом случае зеркальная плоскость ориентирована перпендикулярно
к нотным линейкам. Отраженные ноты кажутся такими, какими они
действительно выглядели бы в зеркале. Начиная от зеркальной плоскости, оригинал проигрывается в обратном направлении.Примерами являются все мажорные и минорные гаммы кроме мелодического вида, а также некоторые отрывки произведений. Например, песня "Священная война" композитора А.В. Александрова и поэта В.И. Лебедева-Кумача, И.С. Бах "Музыкальное приношение".
Слайд 35
Обращение интервала
Это самый редковстречающийся вид. Обращение исходит из
звуковой последовательности, которая испытывает зеркальное отражение в плоскости, параллельной
средней линии нотного стана, так что направления музыкальных интервалов изменяются на обратные. Если мелодия оригинала повышается, то в обращении - понижается на такой же интервал, и наоборот.Примерами могут служить следующие отрывки произведений: "Тарантелла", "Концерт для фортепиано с оркестром" Г. Фоглер.
Слайд 36
Ракоходное обращение
При этом в зеркальной части снова меняется
направленность звукового ряда по высоте. Понижающаяся мелодия ракохода становится
повышающейся, и наоборот.Примером является " Концерт для фортепиано с оркестром" Г. Фоглер.
Слайд 37
Трансляционный вид
Это самый распространенный вид симметрии в музыке.
В этом случае музыкальная фраза (мелодия или более крупные
отрывки музыкального произведения) повторяется, оставаясь неизменной. Но в некоторых случаях возможна асимметрия, то есть отступление от оригинала, для красоты звучания.Примерами служат все песни, в которых куплет (припев) повторяется без изменения несколько раз. Например, песня "Катюша" М. Исаковсковского (слова), Блантера (музыка).
Слайд 38
Секвенция
Разновидность трансляции. Многократное повторение небольшого мотива разных ступеней
лада, как в восходящем, так и в нисходящем направлении.
Беркович
"Второй концерт для фортепиано с оркестром.1 часть"
Слайд 39
Ракоходное обращении с зеркальным отражением
При этом нотный лист
с написанной мелодией можно повернуть на 180°, но мелодия
останется неизменной.Примерами являются отрывки из следующих произведений: Моцарт "Соната № 9". Бетховен "Шесть вариаций",





























