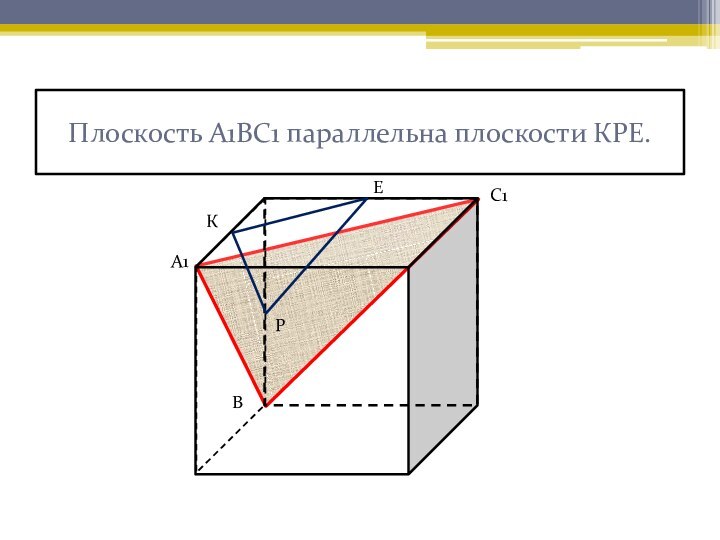
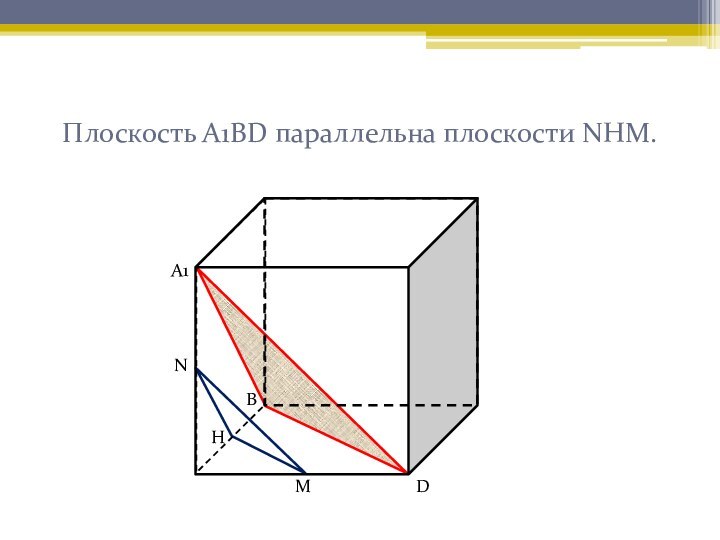
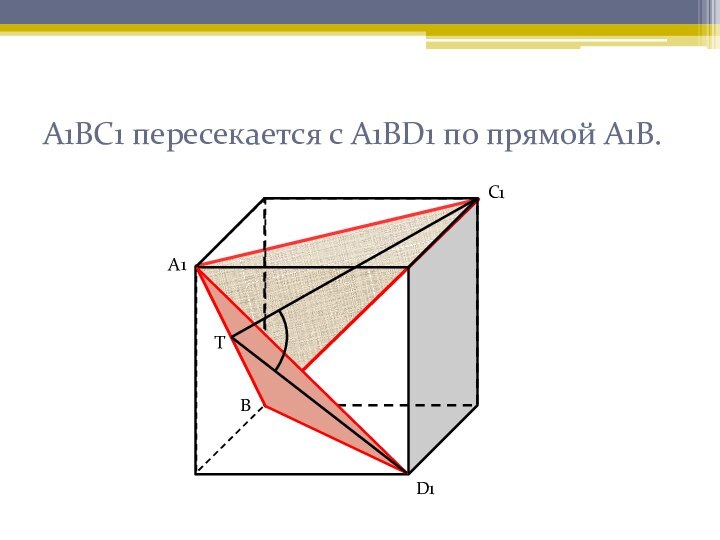
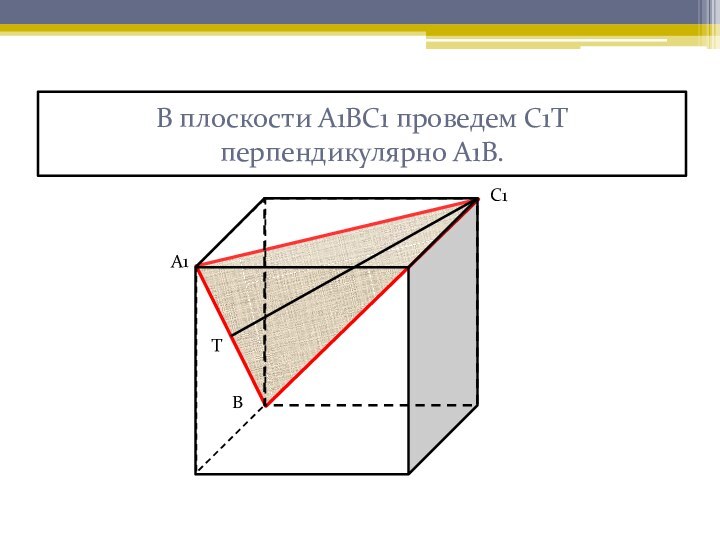
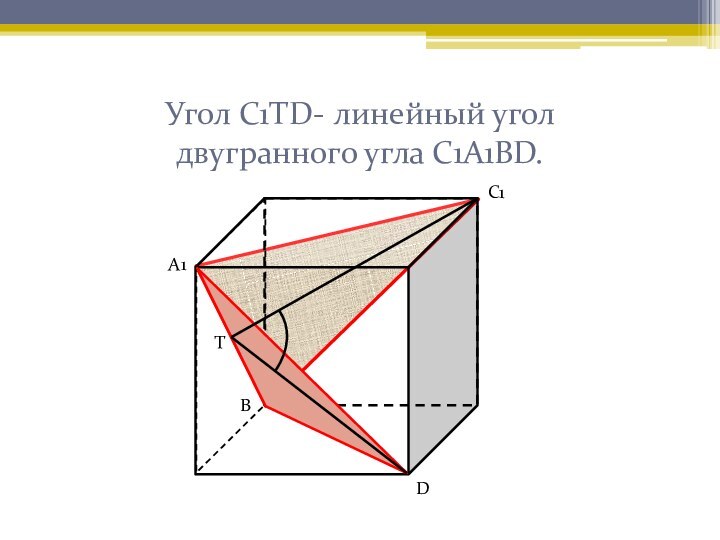
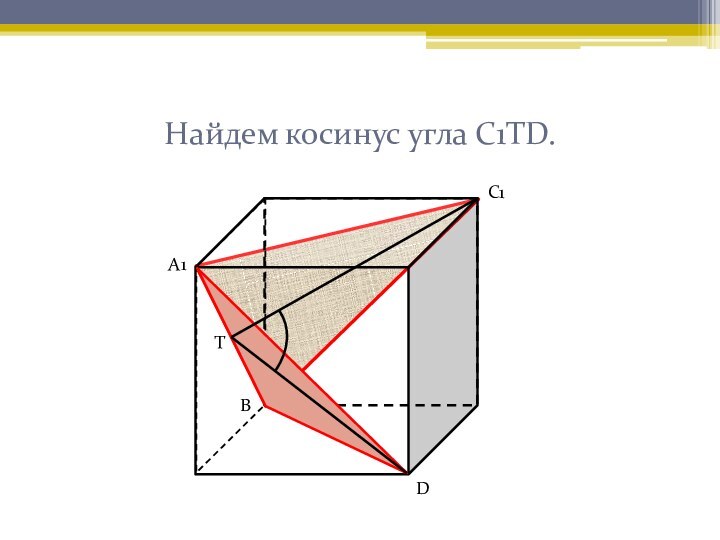
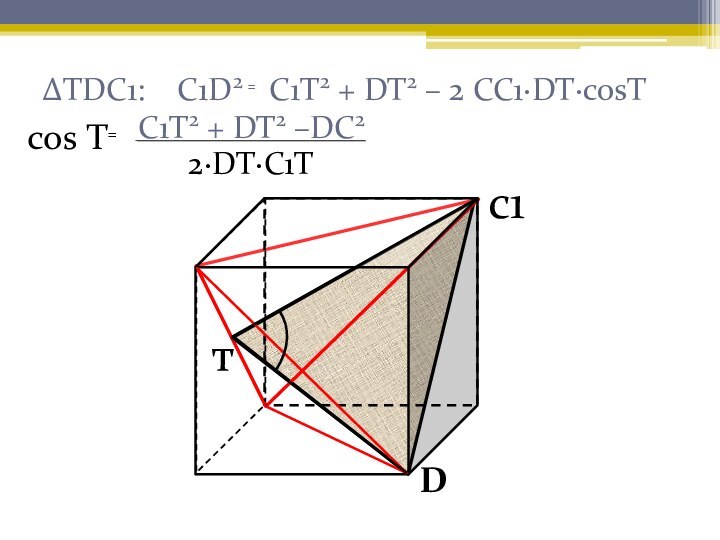
развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают
затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач.Нахождение угла между скрещивающимися прямыми и угла между плоскостями