- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Угол между прямой и плоскостью
Содержание
- 2. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮТеорема. Угол между
- 3. Упражнение 1Прямые a и b образуют с
- 4. Упражнение 2Две плоскости образуют с данной прямой
- 5. Упражнение 3Под каким углом к плоскости нужно
- 6. Упражнение 4Может ли катет равнобедренного прямоугольного треугольника
- 7. Упражнение 5Одна из двух скрещивающихся прямых пересекает
- 8. Упражнение 6В кубе найдите угол между: а)
- 9. Упражнение 7Найдите угол между ребром правильного тетраэдра и не содержащей его гранью.
- 10. Упражнение 8В правильной треугольной пирамиде сторона основания
- 11. Упражнение 9Будут ли в пирамиде боковые ребра
- 12. Упражнение 10Через сторону квадрата проведена плоскость, составляющая
- 13. Упражнение 11Основание равнобедренного треугольника лежит в плоскости
- 14. Скачать презентацию
- 15. Похожие презентации
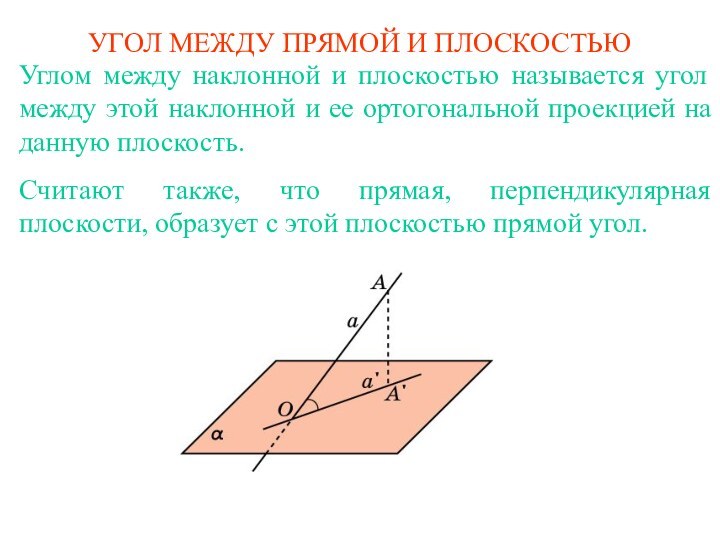
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮТеорема. Угол между наклонной и плоскостью является наименьшим из всевозможных углов между этой наклонной и прямыми, лежащими в данной плоскости.













Слайд 3
Упражнение 1
Прямые a и b образуют с плоскостью
α равные углы. Будут ли эти прямые параллельны?
Ответ: Нет.
Слайд 4
Упражнение 2
Две плоскости образуют с данной прямой равные
углы. Как расположены плоскости относительно друг друга?
Ответ: Параллельны или
пересекаются.
Слайд 5
Упражнение 3
Под каким углом к плоскости нужно провести
отрезок, чтобы его ортогональная проекция на эту плоскость была
вдвое меньше самого отрезка?Ответ: 60о.
Слайд 6
Упражнение 4
Может ли катет равнобедренного прямоугольного треугольника образовать
с плоскостью, проходящей через гипотенузу, угол в 60°? Каков
наибольший угол между катетом и этой плоскостью?Ответ: Нет, 45о.
Слайд 7
Упражнение 5
Одна из двух скрещивающихся прямых пересекает плоскость
под углом 60°, а другая перпендикулярна этой плоскости. Найдите
угол между данными скрещивающимися прямыми.Ответ: 30о.
Слайд 8
Упражнение 6
В кубе найдите угол между: а) диагональю
боковой грани и плоскостью основания; б) диагональю куба и
плоскостью основания; в) диагональю боковой грани и диагональным сечением.Ответ: а) 45о;
в) 30о.
Слайд 10
Упражнение 8
В правильной треугольной пирамиде сторона основания равна
а, а боковое ребро b. Найдите угол наклона бокового
ребра к плоскости основания.
Слайд 11
Упражнение 9
Будут ли в пирамиде боковые ребра равны,
если они образуют равные углы с плоскостью основания?
Ответ:
Да.
Слайд 12
Упражнение 10
Через сторону квадрата проведена плоскость, составляющая с
диагональю квадрата угол 30°. Найдите углы, которые образуют с
плоскостью стороны квадрата, наклонные к ней.Ответ: 45о.
Слайд 13
Упражнение 11
Основание равнобедренного треугольника лежит в плоскости α
(плоскость треугольника не совпадает с плоскостью α). Какой из
углов больше: угол наклона боковой стороны к плоскости α или угол наклона высоты, опущенной на основание треугольника, к плоскости α?Ответ: Угол наклона высоты.