Презентация на тему Умножение и деление степеней 7 класс

шаги современного урока
Организация демонстрации овладение учащимися имеющимися знаниями (шаг

1)

Организация самооценивания обучаемого степенью владения актуальным опытом (шаг 2)

Учебно – практическая задача (шаг 3)

Установление связи, формулирование свойства. Сообщение учащимися пределов познания(шаг 4)

Организация изучения нового материала (шаг 5)

Обобщение изученного, проведение диагностической работы (шаг 6)

различать свойства умножения и деления степеней с натуральным показателем;

применять свойства в случае с одинаковыми основаниями.
Ученик получит возможность уметь выполнять преобразования степеней с разными основаниями и уметь выполнять преобразования в комбинированных заданиях.

уровень воспроизведения посредством выполнения упражнений различного типа
Организовать проверку по

самооценке учащихся посредством тестирования

Шаг 1
а) Актуализация знаний:

1) Верно ли, что: 2 •2• 2 = 23 ;
5 •5•5•5 =45; (-3)3=9, 71=7, 250=25, x •x •x •x •x=4x
Обосновать.
2) Сформулировать определение степени с натуральным показателем.
an = …. n - ? а - ?
3)Верно ли, что: an =a•a•a•a•…•а
(а повторяется n-раз)
bk=b•b•b•b •a…•b (b повторяется k – раз)
Обосновать ответ.

Шаг 2
Тест для самопроверки: (индивидуальная

работа в двух вариантах.)
А1) Представьте произведение 7•7•7•7•x•x•x в виде степени:
(7х4) ; 2) 74 х ; 3) 74х³; 4)7х
А2) Представить в виде произведения степень (-3)3 х2
1)-3• х• х; 2) -3• 3•3 •х•х ; 3)(-3)(-3)(-3)х•х 4) -3•х
A3) Вычислите: -2• 32 + 4• 53
464; 2) 482; 3) 518; 4) -1018
Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.
К тесту даю ключ для самопроверки. Критерии: зачёт – не зачёт.

Шаг 3 и Шаг

4

Задача: 1)вычислите: 2 2 •2 3 = ? 33 •32 •3 =?
2)Упростите: а 2 а 20 = ? b 30 •b 10 •b 15 = ?
В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.
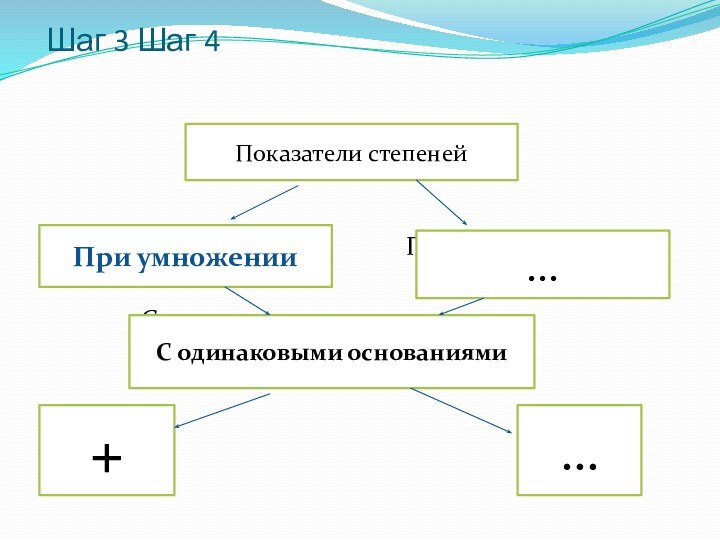
На кластере появляется запись:
показатели степеней
 
При умножении При делении
+ -
С одинаковыми основаниями

 
Формулируется тема урока. Умножение степеней.

показатели степеней

 
При умножении При делении

С одинаковыми основаниями

Показатели степеней

При умножении

...

С одинаковыми основаниями

+

…

Шаг 3,4
Формулируется тема

урока. Умножение степеней.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждения: каким действием проверяется деление?
а5 : а 3 = ? , что а2• а3 = а5
Возвращаюсь к схеме – кластер и дополняем запись - … при делении вычитаем и дописываем тему урока. … и деление степеней.
4)Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: аm• аn = аm+n ; аm : аn = аm-n

показатели

степеней

 
При умножении При делении

С одинаковыми основаниями

Показатели степеней

При умножении

При делении

С одинаковыми основаниями

+

-

Шаг 5
а) По учебнику:

№403 (а, в, д) задания с разными формулировками
№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи.
б) При каком значении m справедливо равенство? а16 • аm = а32 ; хh • х14 = х28; х8 •(*) = х14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а)
Ловушки для учеников: х 3 • х n= х3n ; 3 4 •3 2 = 96;
а 16: а 8 = а2.
6) Обобщение изученного, проведение диагностической работы ( что побуждает учеников, а не учителя изучать данную тему ) (шаг 6)

Шаг 6
6) Обобщение изученного,

проведение диагностической работы ( что побуждает учеников, а не учителя изучать данную тему ) (шаг 6)

Диагностическая работа.
Тест ( ключи поместить на обратной стороне теста).
Варианты заданий:
представьте в виде степени частное х15: х3;
представьте в виде степени произведение (-4)2(-4)5(-4)7; при каком m справедливо равенство а16• аm = а32; найдите значение выражения h0 : h2 при h =0,2; вычислите значение выражения (52 •50 ) : 52.

аргументы I группа : в пользу знания свойств степени,

а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств . Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
Средний человек съедает 32• 10 2 кг огурцов в течение жизни.
Оса способна совершить беспосадочный перелёт на 3,2• 10 2 км.
Когда стекло трескается, трещина распространяется со скоростью около 5 •10 3 км/ч.
Лягушка съедает за свою жизнь более 3 тонн комаров. Используя степень, запишите в кг.
Наиболее плодовитой считается океанская рыба – луна ( Моlа mola), которая откладывает за один нерест до 300000000 икринок диаметром около 1,3 мм. Запишите это число, используя степень.

числами Ферма.
П.19. №403, №408, №417

Используемая литература:
1) Учебник «Алгебра

-7» , авторы Ю.Н.Макарычев, Н.Г.Миндюк и др.
2)Дидактический материал для 7 класса, Л.В.Кузнецова, Л.И. Звавич, С.Б.Суворова.
3)Энциклопедия по математике.
4) Журнал «Квант»
5) СМИ
 

для урока?

и систематизации учащимся информации;
помочь соотнести старые знания с новыми;
обеспечить

учащемуся возможность задуматься о природе изучаемого объекта, научиться формулировать вопросы по мере соотнесения старой и новой информации


Из технологии критического мышления

написать ключевое слово или тезис, который является «сердцем» текста.
Вокруг

«накидать» слова или предложения, выражающие идеи, факты, образы, подходящие для данной темы.
По мере записи, появившиеся слова соединяются прямыми линиями с ключевым  понятием. У каждого из «спутников» в свою очередь тоже появляются «спутники», устанавливаются новые логические связи.

что приходит на ум. Дать волю воображению и интуиции.

Продолжать работу, пока не кончится время или идеи не иссякнут.
Постараться построить как можно больше связей. Не следовать по заранее определенному плану.

некоторые сведения по теме и ориентируются в ряде базовых

понятий, связанных с изучаемым материалом;
«Вопросительные слова» помогают им создать так называемое «поле интереса»;
учащиеся учатся задавать вопросы