какая точка
является началом, какая - концом
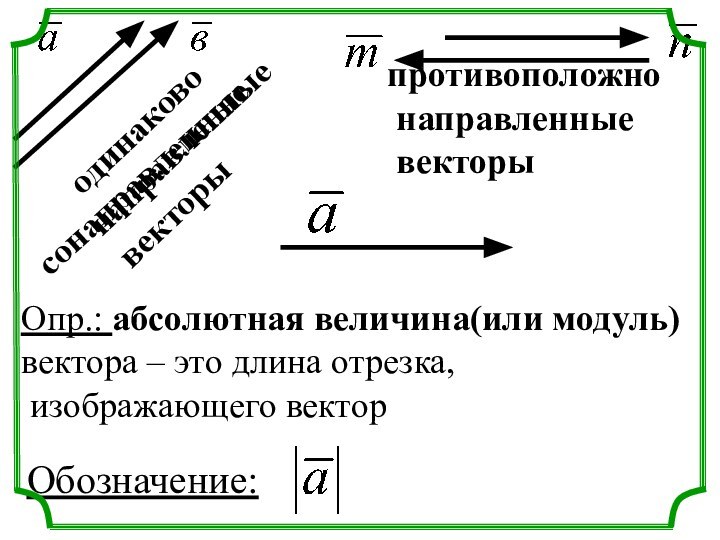
Опр.: Векторная величина
- это величина, которая характеризуется
указанием направления и числового
значения.
М
С
Д
Обозначение: