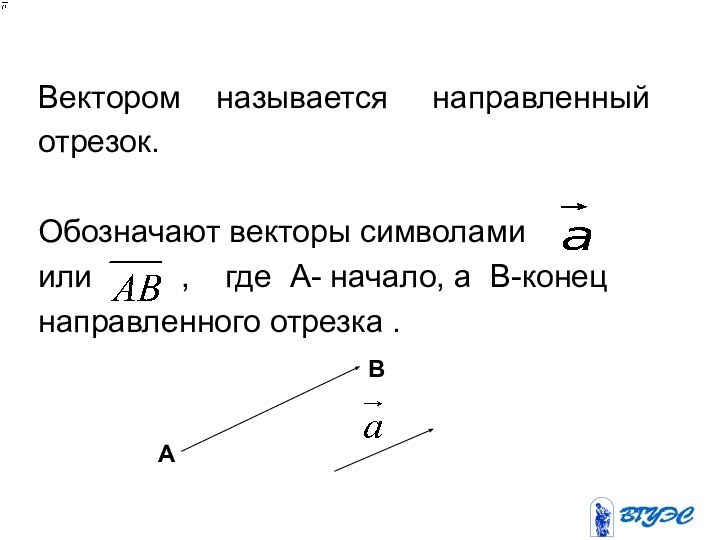
векторы символами
или , где
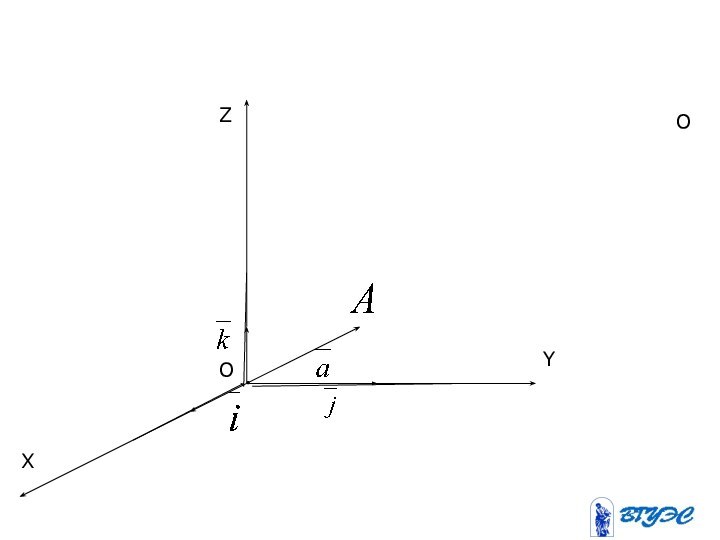
А- начало, а B-конецнаправленного отрезка .
А
В
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











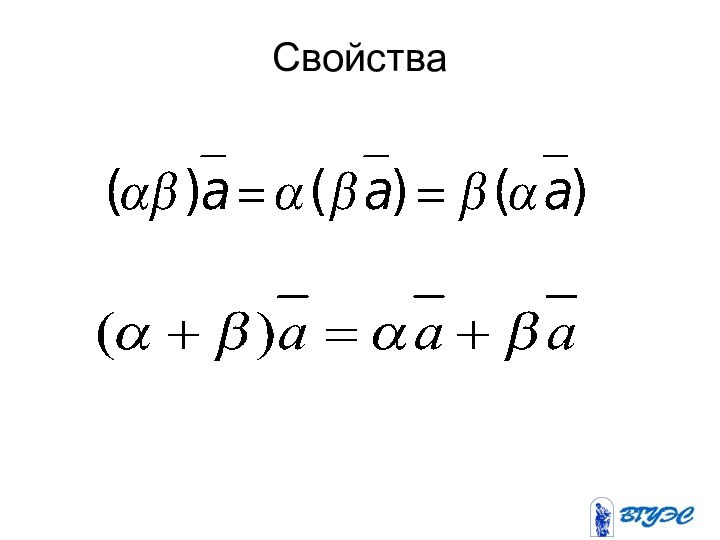
























































А
В
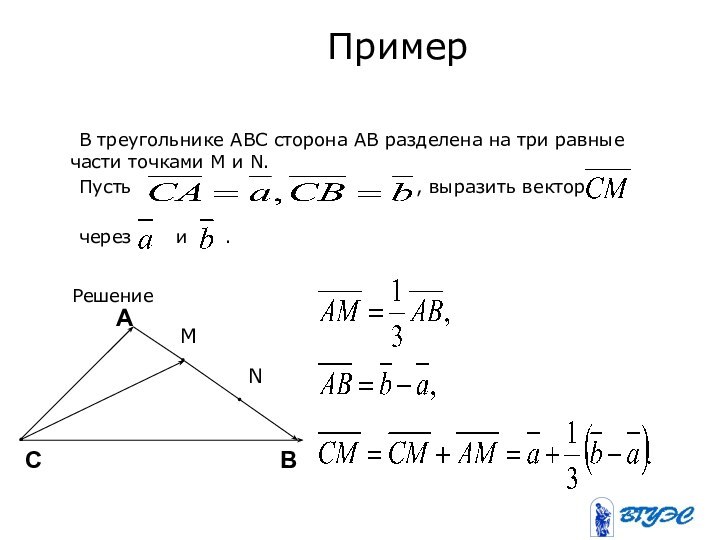
Решение
А
В
С