Слайд 2
Математические понятия, как правило, проходят длительный путь исторического
развития.
Первоначально они возникают в процессе решения практических задач.
Аксиоматический метод в математике
Слайд 3
При этом понятия не имеют еще строгих определений.
Даются расплывчатые приблизительные пояснения, указания на наглядные представления.
Слайд 4
Следующий этап в развитии математических понятий наступает, когда
место наглядных рассмотрений занимают рассуждения, отличающиеся, однако, отсутствием строгой
логичности.
Возникает необходимость в уточнении понятий, установлении связей между ними, в сведении сложных понятий к более простым.
Слайд 5
При аксиоматическом построении какой-нибудь теории поступают так:
Выбирают некоторые
объекты, изучаемые теорией, и некоторые отношения между ними. Эти
объекты и отношения не определяются, а принимаются за исходные и называются основными (неопределяемыми) понятиями рассматриваемой теории. Каждое понятие, которое не содержится в списке основных, должно быть определено.
Слайд 6
Вслед за основными понятиями и отношениями формулируются основные
предложения, их называют аксиомами, которые в данной теории принимаются
без доказательства, и на их основе доказываются другие предложения данной теории – теоремы. В аксиомах дается описание отношений между основными понятиями, они представляют по существу неявные определения основных понятий.
Каждое предложение рассматриваемой теории, которого нет в списке аксиом, должно быть доказано на основе аксиом и ранее доказанных теорем.
Слайд 7
Система аксиом должна быть:
а) непротиворечивой, т.е. мы
должны быть уверены, что делая всевозможные выводы из данной
системы аксиом никогда не придем к противоречию;
б) независимой, т.е. никакая аксиома не должна быть следствием остальных аксиом этой системы.
Первым опытом аксиоматического построения теории можно считать изложение геометрии Евклидом в его «Началах».
Слайд 8
Аксиоматическое определение натурального числа
Как и все математические понятия,
натуральные числа возникли из потребностей практики.
Со временем люди
научились не только называть числа, но и обозначать их, а также выполнять над ними действия. Многие трудности в решении этих проблем были преодолены с созданием в Древней Индии десятичной системы записи чисел и понятия нуля.
Слайд 9
Наука, которая изучает числа и действия над ними,
получила название «арифметика» - от греческого аrithmos - «число».
Во
второй половине 19 века натуральные числа оказались фундаментом всей математической науки, от состояния которого зависела и прочность всего здания математики. Внимание ученых было обращено на построение и логическое обоснование математических теорий числа.
Слайд 10
Известными также считаются понятия множества и другие теоретико-множественные
понятия, а также правила логики
Слайд 11
Элемент, непосредственно следующий за элементом а, обозначается а´
Отношение «непосредственно следовать за» удовлетворяет следующим аксиомам:
Слайд 15
Множество N, для элементов которого установлено отношение «непосредственно
следовать за», удовлетворяющее аксиомам 1- 4, называется множеством натуральных
чисел, а его элементы – натуральными числами.
Слайд 16
Выбирая в качестве множества N некоторое конкретное множество,
на котором задано конкретное отношение «непосредственно следовать за», удовлетворяющее
аксиомам 1-4, получают различные интерпретации (модели) данной системы аксиом:
1) ряд чисел 1, 2, 3, …
2) {O O}, {O О O}, {O O О О}, …
Слайд 17
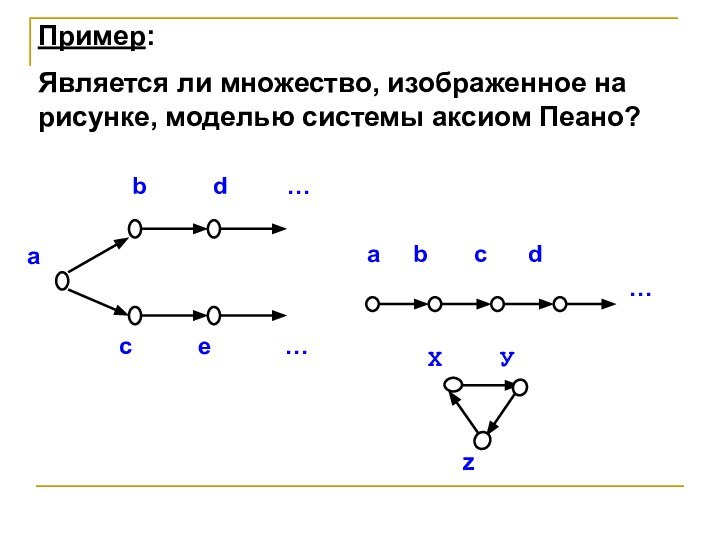
Пример:
Является ли множество, изображенное на рисунке, моделью
системы аксиом Пеано?
Слайд 19
Отношение «непосредственно предшествовать»
Если натуральное число b непосредственно следует
за натуральным числом а, то число а называется непосредственно
предшествующим (или просто предшествующим) числу b.
Свойства отношения «непосредственно предшествовать»
1. Единица не имеет предшествующего натурального числа 2. Каждое натуральное число а 1, имеет предшествующее число b, такое, что b' = а
Слайд 20
Те свойства отношения «непосредственно следовать за, которые отражены
в аксиомах 1 – 4, изучаются в начальных классах
и используются при решении задач. Уже в 1 классе при рассмотрении чисел первого десятка выясняется, как может быть получено каждое число. При этом широко используются понятия «следует», «предшествует», прибавление и вычитание 1.
Слайд 21
Каждое новое число с самого начала выступает как
продолжение ранее изученного отрезка натурального ряда чисел.
Любое натуральное
число может быть получено прибавлением 1 к тому числу, которое встречается при счете перед ним, или вычитанием 1 из числа, которое идет при счете сразу после него.
Любое число на 1 больше предшествующего.
Таким образом, уже в начальных классах учащиеся убеждаются в том, что за каждым числом идет следующее и притом только одно, что натуральный ряд чисел бесконечен.
Слайд 22
Упражнения.
Покажите, что множество целых неотрицательных чисел является
моделью системы аксиом Пеано. Какое число выполняет при этом
роль единицы? Можно ли считать моделью системы аксиом Пеано множество 3, 4, 5, 6, …? множество 3, 6, 9, 12, …?
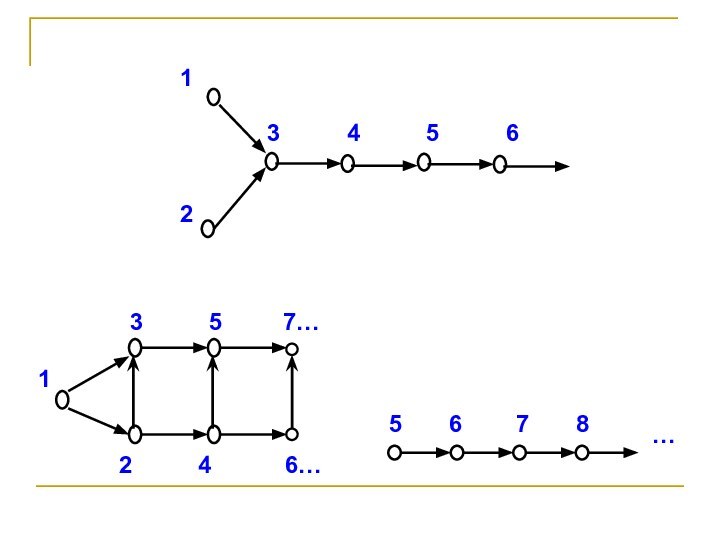
Установите, какие из множеств, приведенных на рисунке, являются моделями системы аксиом Пеано.