- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Возрастание и убывание функции
Содержание
- 2. Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал
- 3. Функция f(x) называется возрастающей на некотором промежутке,
- 4. Функция f(x) называется убывающей на некотором промежутке,
- 5. Теорема Лагранжа Пусть функция f(х) непрерывна
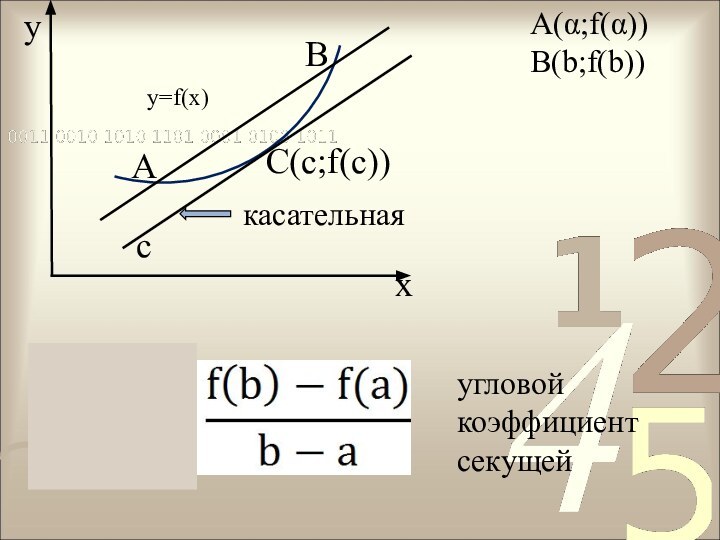
- 6. yxABкасательнаясA(α;f(α))B(b;f(b))y=f(x)угловой коэффициент секущейC(c;f(с))
- 7. Достаточные условия возрастания и убывания функции
- 8. Скачать презентацию
- 9. Похожие презентации
Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал

![Возрастание и убывание функции Числовые промежутки[α;b] – отрезок(α;b) – интервал(α;b] – полуинтервал[α;b) - полуинтервал](/img/tmb/13/1241397/fc1309b26539b9d92d4137d9147577ec-720x.jpg)


![Возрастание и убывание функции Теорема Лагранжа Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема](/img/tmb/13/1241397/c38a5c2b40cc32a36d2cd88f17d9fc78-720x.jpg)

![Возрастание и убывание функции доказательство: Пусть х1 и х2 - произвольные точки отрезка [α;b] , такие,](/img/tmb/13/1241397/46175200b4aa47bb85ee2c5115f64284-720x.jpg)
Слайд 3 Функция f(x) называется возрастающей на некотором промежутке, если
большему значению аргумента соответствует большее значение функции.
x1 >
x2 f(x1 ) > f(x2)Слайд 4 Функция f(x) называется убывающей на некотором промежутке, если
большему значению аргумента соответствует меньшее значение функции.
x1 >
x2 f(x1 ) < f(x2)
Слайд 5
Теорема Лагранжа
Пусть функция f(х) непрерывна на
отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует
точка с € (α;b), такая, чтоf(b) – f(α) = f ′(c) (b - α)
Слайд 7
Достаточные условия возрастания и убывания функции
Пусть
функция f(х) непрерывна на отрезке [α;b] и дифференцируема на
интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) ,то функция f(x) возрастает на отрезке [α;b] ,
а если f′(x)<0 для всех х € (α;b) ,
то функция f(x) убывает на отрезке [α;b] .