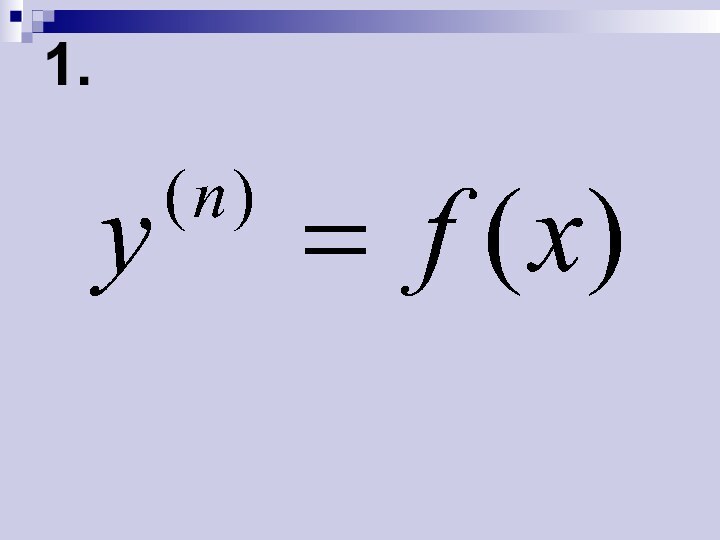Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Дифференциальные уравнения высших порядков

Содержание

1. Общие сведения.
Глава 2. Дифференциальные уравнения высших порядков. 1. Общие сведения. Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным Теорема: Дано дифференциальное уравнение 2.Типы уравнений, допускающих понижение порядка. 1. 2. Дифференциальное уравнение не содержащее явно 3. Уравнение вида 4. Если левая часть уравнения есть точная правая, то порядок уравнения поднимается Линейное дифференциальное уравнение высшего порядка. Линейным дифференциальным уравнением n-го порядка называется уравнение вида: Теорема Пусть коэффициент , . Определение: Уравнение вида называется линейным однородным дифференциальным уравнением. Определение. Обозначим линейную часть уравнения через , Свойства линейного дифференциального оператора.1.Постоянный множитель можно выносить за знак оператора, то есть Определение: Линейное дифференциальное однородное уравнение можно записать в виде Теоремы о свойствах частичных решений Теорема1. Если функция является решением уравнения Теорема2. Если функции и являются решениями уравнения Теорема3. Если - частные решения Линейная зависимость и независимость функций. Определитель Вронского и его применение. Определение. Система функций определенных и непрерывных на Теорема. Если уравнение линейно зависимо, то хотя бы одну из них можно выразить через остальные. Если функции системы дифференцируемы n-1 то из них можно построить определитель n-го Теорема1.Если функции линейно зависимы, Теорема 2.Если - линейно независимые функции, Определение.Систему частных решений линейного однородного дифференциального Теорема.Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством фундаментальных систем. Теорема Если функции образуют фундаментальную систему Линейное однородное уравнение с постоянным коэффициентом. Определение. Уравнение вида Определение. называется характеристическим членом линейного однородного дифференциального уравнения. Определение. Уравнение называется характеристическим уравнением линейного однородного дифференциального уравнения. Все корни уравнения действительны и различны линейная комбинация является общим решением линейного однородного дифференциального уравнения. Все корни различны, но среди них есть комплексные формулы Эйлера : паре комплексных сопряженных корней можно поставить в соответствие частных решений Доказать самостоятельно линейную независимость системы частных решений При доказательстве нигде не учитывается, что - Вывод: Задача нахождения общего решения линейного однородного дифференциального уравнения n – го 3.Линейные неоднородные дифференциальные уравнения. Определение Линейным неоднородным дифференциальным уравнением называется уравнение вида Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения): Общее решение линейного Теорема2: Если правая часть неоднородного уравнения есть сумма двух функций, т.е.
Слайды презентации

Слайд 2 1. Общие сведения.

1. Общие сведения.

Слайд 3 Определение.
Дифференциальное уравнение содержащее производную функции двух и

Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется

более порядков, называется дифференциальным уравнением порядка высшее первого.
Уравнение порядка

“ ”- или




Слайд 4 Теорема:
Дано дифференциальное уравнение

Теорема: Дано дифференциальное уравнение и система

и система начальных

условий , ,…., Если функция непрерывна в окрестностях начального условия и имеет непрерывные частные производные по , то существует и притом единственное решение уравнения, определенное и непрерывное в некотором интервале содержащем , и удовлетворяющее заданной системе начальных условий.








Слайд 5 2.Типы уравнений, допускающих понижение порядка.

2.Типы уравнений, допускающих понижение порядка.

Слайд 6 1.

1.

Слайд 7 2.
Дифференциальное уравнение

2. Дифференциальное уравнение не содержащее явно и младших

не содержащее явно и младших производных до

(k-1) порядка включительно, допускает понижение порядка на k единиц





Слайд 8 3.
Уравнение вида

3. Уравнение вида также допускает

также

допускает понижение порядка путем замены обоих переменных.




Слайд 9 4.
Если левая часть уравнения есть точная правая,

4. Если левая часть уравнения есть точная правая, то порядок уравнения

то порядок уравнения поднимается на единицу путем непосредственного интегрирования.

(Это уравнение встречается редко, но к этому виду приводятся некоторые уравнения.)

Слайд 10 Линейное дифференциальное уравнение высшего порядка.

Линейное дифференциальное уравнение высшего порядка.

Слайд 11 Линейным дифференциальным уравнением n-го порядка называется уравнение вида:

Линейным дифференциальным уравнением n-го порядка называется уравнение вида:



Слайд 12 Теорема
Пусть коэффициент ,

Теорема Пусть коэффициент , . Линейное дифференциальное уравнение

. Линейное дифференциальное уравнение непрерывно на

некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и любой системе начальных условий, если только значение принадлежит интервалу (a;b).






Слайд 13 Определение:
Уравнение вида

называется

Определение: Уравнение вида называется линейным однородным дифференциальным уравнением.

линейным однородным дифференциальным уравнением.

Слайд 14 Определение.
Обозначим линейную часть уравнения через

Определение. Обозначим линейную часть уравнения через ,

,

. .
Выражение называется линейным дифференциальным оператором от функции .






Слайд 15 Свойства линейного дифференциального оператора.
1.Постоянный множитель можно выносить за

Свойства линейного дифференциального оператора.1.Постоянный множитель можно выносить за знак оператора, то

знак оператора, то есть для любого n размерной дифференциальной

функции
- свойство однородности.
2.Оператор от суммы двух функций и равен сумме операторов от каждого из слагаемых в отдельности, то есть для любых n раз дифференцируемых функций и верно равенство:
- свойство аддитивности






Слайд 16 Определение:
Линейное дифференциальное однородное уравнение можно записать в

Определение: Линейное дифференциальное однородное уравнение можно записать в виде

виде

Слайд 17 Теоремы о свойствах частичных решений

Теоремы о свойствах частичных решений

Слайд 18 Теорема1.
Если функция является решением уравнения

Теорема1. Если функция является решением уравнения , то

, то и функция

есть решение этого уравнения.




Слайд 19 Теорема2.
Если функции и

Теорема2. Если функции и являются решениями уравнения

являются решениями уравнения ,

то и функция есть решение этого уравнения.






Слайд 20 Теорема3.
Если

Теорема3. Если - частные решения линейного однородного дифференциального

- частные решения линейного однородного дифференциального уравнения, то

их линейная комбинация
есть также решение этого уравнения.



Слайд 21 Линейная зависимость и независимость функций. Определитель Вронского и

Линейная зависимость и независимость функций. Определитель Вронского и его применение.

его применение.

Слайд 22 Определение.
Система функций

Определение. Система функций определенных и непрерывных на отрезке [a;b]

определенных и непрерывных на отрезке [a;b] называется линейно зависимой

на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) .







Слайд 23 Теорема.
Если уравнение линейно зависимо, то хотя бы

Теорема. Если уравнение линейно зависимо, то хотя бы одну из них можно выразить через остальные.

одну из них можно выразить через остальные.

Слайд 24 Если функции системы дифференцируемы n-1 то из них

Если функции системы дифференцируемы n-1 то из них можно построить определитель

можно построить определитель n-го порядка, который имеет вид



Этот определитель

является функцией от х и обозначается
Этот определитель называется определителем Вронского




Слайд 25 Теорема1.
Если функции

Теорема1.Если функции линейно зависимы, то определитель Вронского тождественно равен 0.

линейно зависимы, то определитель Вронского тождественно равен

0.


Слайд 26 Теорема 2.
Если

Теорема 2.Если - линейно независимые функции, удовлетворяющие некоторому

- линейно независимые функции, удовлетворяющие некоторому однородному дифференциальному уравнению

n-го порядка, то определитель системы не обращается в ноль ни в одной точке.



Слайд 27 Определение.
Систему частных решений

Определение.Систему частных решений линейного однородного дифференциального уравнения n-го

линейного однородного дифференциального уравнения n-го порядка называют фундаментальной,

если она состоит из n независимых функций.


Слайд 28 Теорема.
Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством

Теорема.Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством фундаментальных систем.

фундаментальных систем.

Слайд 29 Теорема
Если функции

Теорема Если функции образуют фундаментальную систему решений уравнения,то

образуют фундаментальную систему решений уравнения

,то их линейная комбинация

- является общим решением этого уравнения.




Слайд 30 Линейное однородное уравнение с постоянным коэффициентом.

Линейное однородное уравнение с постоянным коэффициентом.

Слайд 31 Определение.
Уравнение вида

Определение. Уравнение вида

, г де =const, называется линейным однородным дифференциальным уравнением с постоянным коэффициентом.



Слайд 32 Определение.

называется характеристическим членом линейного однородного дифференциального

Определение. называется характеристическим членом линейного однородного дифференциального уравнения.

уравнения.

Слайд 33 Определение.
Уравнение

называется характеристическим уравнением линейного однородного дифференциального

Определение. Уравнение называется характеристическим уравнением линейного однородного дифференциального уравнения.

уравнения.

Слайд 34 Все корни уравнения


действительны и различны


Все корни уравнения действительны и различны

Слайд 35
линейная комбинация


является общим решением линейного однородного дифференциального

линейная комбинация является общим решением линейного однородного дифференциального уравнения.

уравнения.

Слайд 36 Все корни различны, но среди них есть комплексные

Все корни различны, но среди них есть комплексные



Слайд 37 формулы Эйлера :


формулы Эйлера :

Слайд 38 паре комплексных сопряженных корней

можно поставить в

паре комплексных сопряженных корней можно поставить в соответствие частных решений

соответствие частных решений



Слайд 39 Доказать самостоятельно линейную независимость системы частных решений

Доказать самостоятельно линейную независимость системы частных решений

Слайд 40 При доказательстве нигде не учитывается, что

При доказательстве нигде не учитывается, что - действительное число

- действительное число поэтому когда пара

корней является двойной, то ей соответствует четыре частных решения следующих видов:






Слайд 41 Вывод:
Задача нахождения общего решения линейного однородного дифференциального

Вывод: Задача нахождения общего решения линейного однородного дифференциального уравнения n –

уравнения n – го порядка с постоянным коэффициентом сводится

к нахождению всех корней алгебраического уравнения n-ой степени.

Слайд 42 3.Линейные неоднородные дифференциальные уравнения.

3.Линейные неоднородные дифференциальные уравнения.

Слайд 43 Определение
Линейным неоднородным дифференциальным уравнением называется уравнение вида

Определение Линейным неоднородным дифференциальным уравнением называется уравнение вида

Слайд 44 Теорема (о структуре общего решения линейного неоднородного дифференциального

Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения): Общее решение

уравнения):
Общее решение линейного неоднородного дифференциального уравнения представляет сумму

частного решения этого уравнения и общего решения соответствующего однородного (при g=0), .


  • Имя файла: differentsialnye-uravneniya-vysshih-poryadkov.pptx
  • Количество просмотров: 103
  • Количество скачиваний: 0
- Предыдущая Конус. Стереометрия
Следующая - Буря ураган

Похожие презентации

Определение подобных треугольников Определение подобных треугольников 104
Формула одновременного движения Формула одновременного движения 173
Трехзначные числа. Запись трехзначных чисел в виде суммы разрядных слагаемых Трехзначные числа. Запись трехзначных чисел в виде суммы разрядных слагаемых 167
Действия с десятичными дробями Действия с десятичными дробями 116
Окружность и круг 5 класс Окружность и круг 5 класс 140
Компоненты сложения и вычитания. Презентация 1 класс презентация к уроку по математике (1 класс) по теме Компоненты сложения и вычитания. Презентация 1 класс презентация к уроку по математике (1 класс) по теме 126
Методи розподілу витрат на змінну та постійну частини. (Тема 4) Методи розподілу витрат на змінну та постійну частини. (Тема 4) 108
Презентация к творческому проекту по математике на тему: Математика и живопись Презентация к творческому проекту по математике на тему: Математика и живопись 207
Презентация по математике в 6 классе на тему Симметрия в окружающем мире Презентация по математике в 6 классе на тему Симметрия в окружающем мире 156
Математические диктанты Математические диктанты 164
урок Математика 1 класс Ломаная линия план-конспект урока по математике (1 класс) по теме урок Математика 1 класс Ломаная линия план-конспект урока по математике (1 класс) по теме 121
Число и цифра 6 презентация к уроку по математике по теме Число и цифра 6 презентация к уроку по математике по теме 115
Числовые и буквенные выражения Числовые и буквенные выражения 118
Алгоритмически неразрешимые проблемы. Машина Тьюринга Алгоритмически неразрешимые проблемы. Машина Тьюринга 158
Презентация по математике Матрица. Типы матриц. Действия над матрицами Презентация по математике Матрица. Типы матриц. Действия над матрицами 159
Презентация по математике на тему Построение графиков функций и уравнений с модулем Презентация по математике на тему Построение графиков функций и уравнений с модулем 109
Сложение и вычитание дробей с одинаковыми знаменателями Сложение и вычитание дробей с одинаковыми знаменателями 91
Образовательный квест Путешествие с Райдером и щенками к королю Математики. презентация к уроку по математике (старшая группа) по теме Образовательный квест Путешествие с Райдером и щенками к королю Математики. презентация к уроку по математике (старшая группа) по теме 124
Разнообразный мир линий Разнообразный мир линий 96
Презентация по математике Цифра 7 Презентация по математике Цифра 7 107
Занимательная математика презентация урока для интерактивной доски по математике Занимательная математика презентация урока для интерактивной доски по математике 110
Презентация для ГМО учителей математики Применение традиционной технологии на уроках математики Презентация для ГМО учителей математики Применение традиционной технологии на уроках математики 116
Игра Математический ринг 5- 6 класс Игра Математический ринг 5- 6 класс 133
Тайны совершенных чисел Тайны совершенных чисел 127
Моя математика Моя математика 131
Перемещение. Путь. Траектория 9 класс Перемещение. Путь. Траектория 9 класс 97
Как построить график функции y = f(x+1)+m, если известен график функции y = f(x) Как построить график функции y = f(x+1)+m, если известен график функции y = f(x) 96
Повторение планиметрии Повторение планиметрии 177
Квадратный трехчлен и его корни Квадратный трехчлен и его корни 113
Презентация по математике на тему Меры времени Презентация по математике на тему Меры времени 108