- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вписанные шары
Содержание
- 2. Историческая справка: Пифагор (580 до
- 3. Настоящий расцвет Геометрии в Греции начинается с
- 4. Первый дошедший
- 5. Работы Архимеда (287-212) относятся преимущественно к так
- 6. Понятие термина «сфера» и «шар».Определение 1.
- 7. Комбинации шара с различными фигурами
- 8. Комбинация шара с другими телами. 1.
- 9. Комбинация шара с призмой:Теорема 1. Шар можно
- 10. Комбинация шара с круглыми телами. Теорема
- 11. Шары Данделена. Данделен Жерминаль Пьер
- 12. Задачи: 1.
- 13. Решение: В этой, как и в других
- 14. 1) площадь одной из боковых граней2) полная
- 15. 2.
- 17. 3) По условию задачи имеем
- 18. Использование знаний о вписанных шарах.Египетские пирамиды.Самая высокая
- 19. Известно несколько теорий по поводу отношений между
- 20. Вывод:В данной работе была рассмотрена тема «вписанные
- 21. Скачать презентацию
- 22. Похожие презентации
Историческая справка: Пифагор (580 до Р. X.), основал в Италии известную школу, носящую его имя. Пифагору принадлежат: замечание о несоизмеримости диагонали и стороны квадрата, теорема о квадрате гипотенузы, свойство круга быть maximum между фигурами



















Слайд 3 Настоящий расцвет Геометрии в Греции начинается с Платона
(430-347). Платон первый указал на важное значение Геометрии в
кругу других наук, написав на дверях академии: "пусть не знающий геометрии не входит сюда". Не будучи геометром, по специальности, Платон способствовал прогрессу Геометрии введением в науку так называемого аналитического метода, изучением свойств конических сечений и установкой плодотворного учения о геометрических местах.Слайд 4 Первый дошедший
до нас полный трактат по Геометрии, представляющий собрание и систематизацию открытий греческих математиков, принадлежит знаменитому александрийскому геометру Эвклиду (285 до Р. X.). Это бессмертное сочинение носит название"Начала" (Elementa) и представляет полный курс так называемой элементарной Геометрии, имеющий, за весьма немногими исключениями, объем, в котором Геометрия входит в настоящее время в круг преподавания средних учебных заведений. Новинкой этого трактата является метода доказательства, состоящая в доказательстве абсурдности противоположного. В нем автор обнаруживает образцовую последовательность изложения и строгость доказательств.
Слайд 5 Работы Архимеда (287-212) относятся преимущественно к так называемой
Геометрии меры.
У Архимеда нет такой основополагающей работы, как
«Элементы» у Евклида. Дошедшие до нас сочинения Архимеда (их тринадцать) решают частные проблемы. Это «О сфере и цилиндре», «Измерение круга», «Коноиды и сфероиды», «Спирали», «Равновесие плоскостей», «Квадратура параболы», «Плавающие тела», «Книга лемм», «Стомахион» (геометрические головоломки), «Псаммит», «Скотская проблема», наконец, «Метод», открытый лишь в 1907 г. датским ученым Иоганом Гейбергом (1854—1928) в константинопольском палимпсесте и «Правильный семиугольник» (в 1926 г.).
Слайд 6
Понятие термина «сфера» и «шар».
Определение 1.
Сфера
радиуса R есть множество точек пространства, удаленных от данной
точки на положительное расстояние R. В координатном пространстве сфера с центром O(a;b;c) и радиусом R задается уравнением:(x-a)2+(y-b)2+(z-c)2=R2
Сфера является фигурой вращения. При вращении полуокружности радиуса R вокруг её диаметра получается сфера радиуса R. Определение 2.
Шар радиуса R есть геометрическое место точек пространства, удаленных от данной точки не более чем на расстояние R (R>0).
Слайд 7 Комбинации шара с различными фигурами
Пирамида и шар:
Определение 1.
Пирамида называется описанной около шара (сферы), если все её грани касаются поверхности шара - сферы.Теорема 1.
Центр вписанной в пирамиду сферы лежит на пересечении биссекторных плоскостей внутренних двугранных углов пирамиды.
Теорема 2.
Для того чтобы в пирамиду можно было вписать шар (сферу), необходимо и достаточно, чтобы биссекторные плоскости внутренних двугранных углов пирамиды пересекались в одной точке.
Теорема 3.
В любой тетраэдр (треугольную пирамиду) можно вписать шар (сферу).
Теорема 4.
В любую правильную пирамиду можно вписать шар (сферу).
Теорема 5.
В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований.
Слайд 8
Комбинация шара с другими телами.
1. Шар называется вписанным
в многогранник, если поверхность шара касается всех граней многогранника.
2.
Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус) – описанным около шара, если поверхность шара касается оснований (основания) и всех образующих цилиндра, усеченного конуса (конуса).
Слайд 9
Комбинация шара с призмой:
Теорема 1.
Шар можно вписать
в прямую призму в том и только в том
случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.Следствие 1.
Центр шара, вписанного в прямую призму, лежит в середине высоты призмы, проходящей через центр окружности, вписанной в основание.
Следствие 2.
Шар, в частности, можно вписать в прямые: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии Н = 2r, где Н – высота призмы, r – радиус круга, вписанного в основание.
Слайд 10
Комбинация шара с круглыми телами.
Теорема 1.
1.В цилиндр
(прямой круговой) можно вписать шар в том и только
в том случае, если цилиндр равносторонний.2. В цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания.
Теорема 2.
1. В любой конус (прямой круговой) можно вписать шар.
2.Сфера называется вписанной в конус, если она касается образующих конуса и его основания.
3. В любой конус можно вписать сферу.
Теорема 3.
1.В усеченный конус (прямой круговой) можно вписать шар в том и только в том случае, если его образующая равна сумме радиусов оснований.
2.Сфера называется вписанной в усеченный конус, если она касается всех образующих и обоих оснований конуса.
3.Очевидно справедливо утверждение: в усеченный конус можно вписать сферу тогда и только тогда, когда образующая усеченного конуса равна сумме радиусов оснований. Тогда диаметр сферы равен высоте усеченного конуса.
Слайд 11
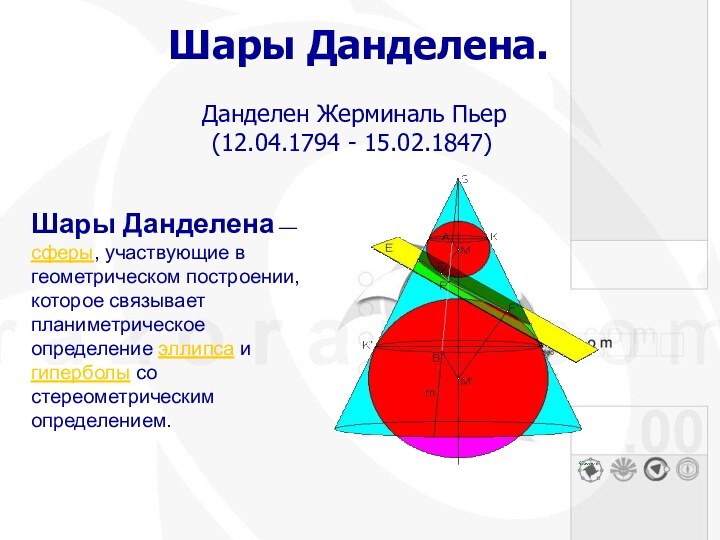
Шары Данделена.
Данделен Жерминаль Пьер
(12.04.1794 - 15.02.1847)
Шары Данделена
— сферы, участвующие в геометрическом построении, которое связывает планиметрическое определение эллипса и гиперболы со стереометрическим определением.
Слайд 12
Задачи:
1.
Условие.
Найти объем шара, вписанного в правильную
треугольную пирамиду с ребром основания, равным а, и плоским углом при вершине, равным α.
Слайд 13
Решение:
В этой, как и в других аналогичных
задачах, полезно использовать общее замечание, относящееся к вычислению радиуса
шара, вписанного в выпуклый многогранник (т. е. касающегося каждой из граней). Представим себе, что в центре шара мы поместим вершину ряда пирамид, основаниями которых будут грани многогранника. Радиус шара будет служить высотой каждой из этих пирамид. Тогда объем многогранника V можно вычислить как сумму объемов указанных пирамид; объем каждой из них будет равен одной трети произведения ее высоты (т. е. радиуса вписанного в многогранник шара) на площадь ее основания (т. е. на площадь соответствующей грани многогранника). Сумма объемов пирамид будет равна одной трети произведения радиуса вписанногошара на полную поверхность многогранника: . В нашем
случае площадь основания пирамиды (т.к. основание
пирамиды – правильный треугольник).
Слайд 14
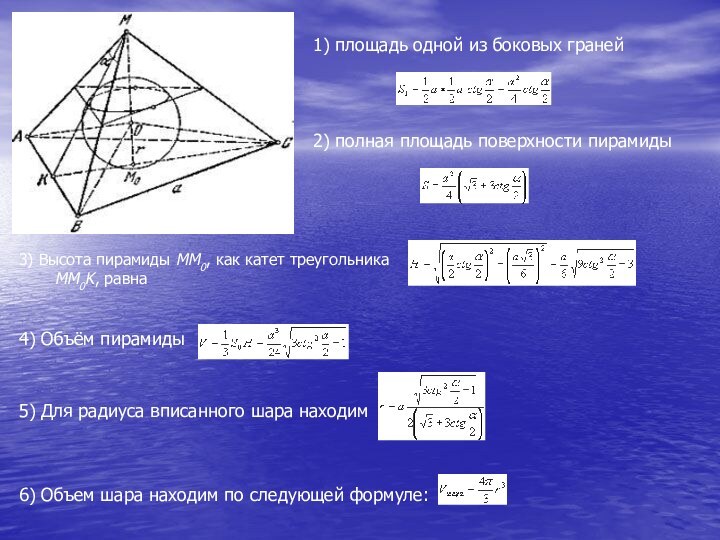
1) площадь одной из боковых граней
2) полная площадь
поверхности пирамиды
3) Высота пирамиды MM0, как катет треугольника
MM0K, равна4) Объём пирамиды
5) Для радиуса вписанного шара находим
6) Объем шара находим по следующей формуле:
Слайд 15 2.
Условие:
Боковая поверхность
конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, еслирадиус шара равен .
Слайд 16
Решение:
1) Введем для удобства угол, а между высотой и образующей конуса. Найдем для высоты, радиуса основания и образующей конуса выражения
2) Площадь боковой поверхности конуса равна
Слайд 17
3) По условию задачи имеем уравнение
4)
откуда для
получается квадратное уравнение
5) решая его, имеем
для два значения:
и
6) которым отвечают два условия поставленной задачи
и
Ответ:
,
.
Слайд 18
Использование знаний о вписанных шарах.
Египетские пирамиды.
Самая высокая пирамида
мира представляет собой еще и самый исследованный в геометрическом
отношении памятник. Тем не менее, в египтологии не существует теории, которая бы объясняла конкретные значения параметров пирамид. В самом деле, нельзя же думать, что такое огромное и чрезвычайно сложное сооружение имеет высоту, которая получилась случайно, или что между фараонами проводилось соревнование "чья пирамида выше".Слайд 19 Известно несколько теорий по поводу отношений между параметрами
пирамид.
Как ни странно, но древние архитекторы Египта уклонились
от идеальной формы пирамиды. Чтобы понять, зачем они это сделали, впишем в пирамиду шар и вычислим его радиус. В идеальной пирамиде он будет равен 55,9720 м, а в пирамиде с измеренным углом 51°51'30" – 56,010 м. А теперь поделим высоту пирамиды "золотым сечением" так, чтобы меньшая часть была внизу:
Она будет равна 56,034 м.
Таким образом, центр вписанного шара совпадает с точкой "золотого сечения" высоты пирамиды. А радиус шара равен 56 м. Ровно!
Полезно выразить радиус вписанного шара в канонических царских локтях в 28 пальцев (0,5185 (185).... м):
56 м : 0,5185 (185).... м = 108 локтей.
Хороший и понятный результат.
Точное значение 56,00 м радиус вписанного шара будет иметь при угла в 51°51' и высоте пирамиды 146,42 м. Таким образом, точное выражение радиуса числом 56 в метрах, может быть достаточно сильным мотивом для выбора угла. Но почему 56, не потому ли, что 56 м = 108 локтей? Ключ к этой тайне пирамид лежит в числе рядов кладки и их высоте. Археологи дважды проводили замеры и расчеты. Общее число рядов кладки до вершины геометрической пирамиды – их 220.
Верхняя поверхность ряда № 215 образует площадку, которая играет важную роль в геометрии пирамиды. Длина стороны квадратной площадки составит 4,24 м. Примечательно, что идеальная пирамида (с α = 51°49'38",25) будет иметь на этом уровне площадку 3,98 м х 3,98 м. Четырехметровая (4,00 м х 4,00 м) площадка будет при α = 51°49'43",5 и высоте 146,54 м, что нечувствительно отличается от идеальной пирамиды.





























