- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вписанные в окружность и описанные около окружности четырехугольники
Содержание
- 2. Четырехугольник, все вершины которого лежат на окружности,
- 3. Теорема 1. Сумма противоположных углов
- 4. Теорема обратная теореме 1. Если
- 5. Если все стороны четырехугольника касаются окружности, то
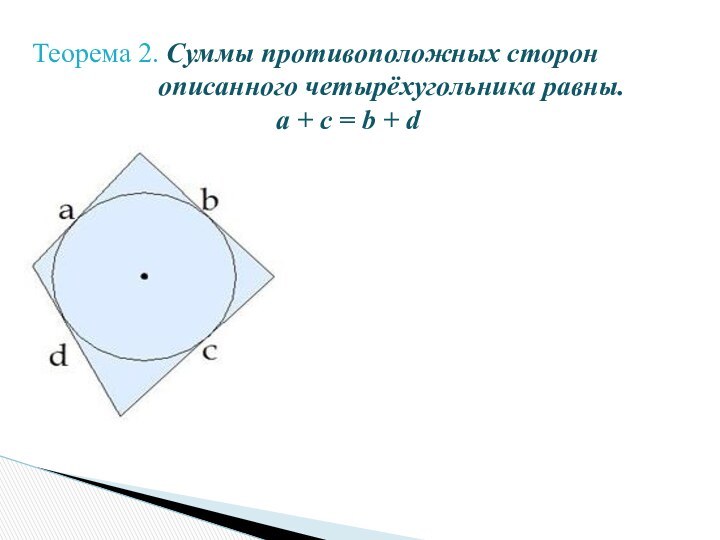
- 6. Теорема 2. Суммы противоположных сторон
- 7. Теорема обратная теореме 1. Если суммы противоположных
- 8. 1. Четырёхугольник ABCD описан около окружности с центром О. Найдите сумму углов АОВ и COD. ABCDO
- 9. Скачать презентацию
- 10. Похожие презентации
Четырехугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырехугольника.







Слайд 2 Четырехугольник, все вершины которого лежат на окружности, называется вписанным в
эту окружность, а окружность называется описанной около четырехугольника.
Слайд 4 Теорема обратная теореме 1. Если сумма
противоположных углов четырехугольника равна 180°, то около него можно
описать окружность.Следствие. Не во всякий четырёхугольник можно вписать окружность.