Презентация на тему Введение в мир фракталов

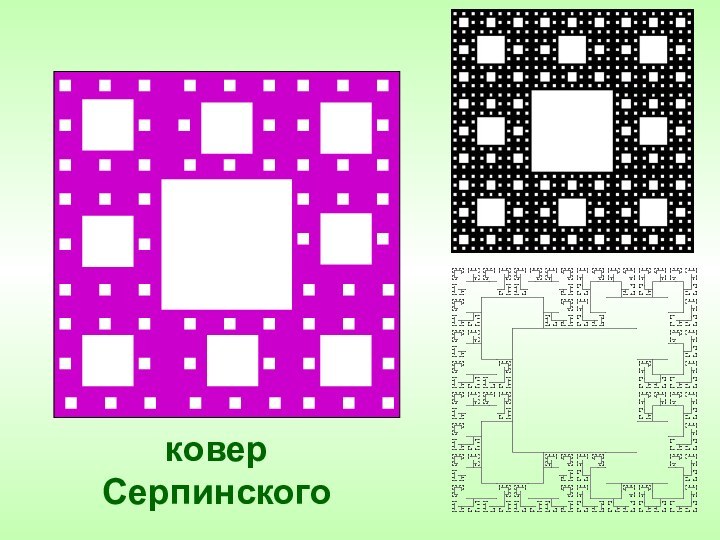
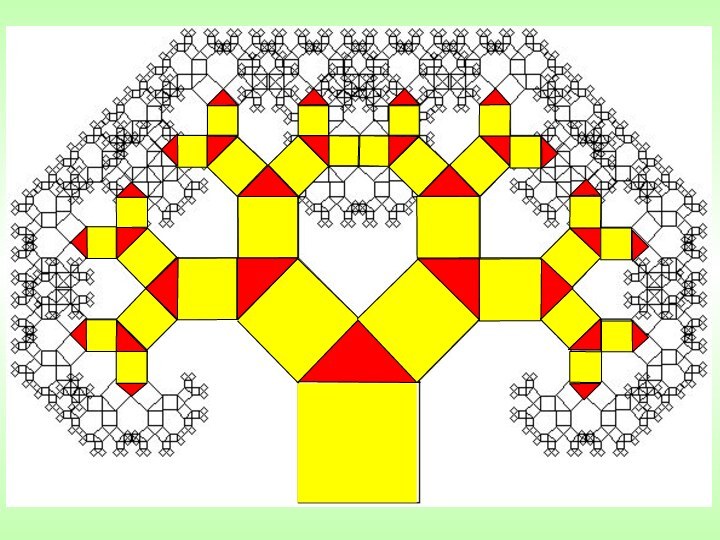
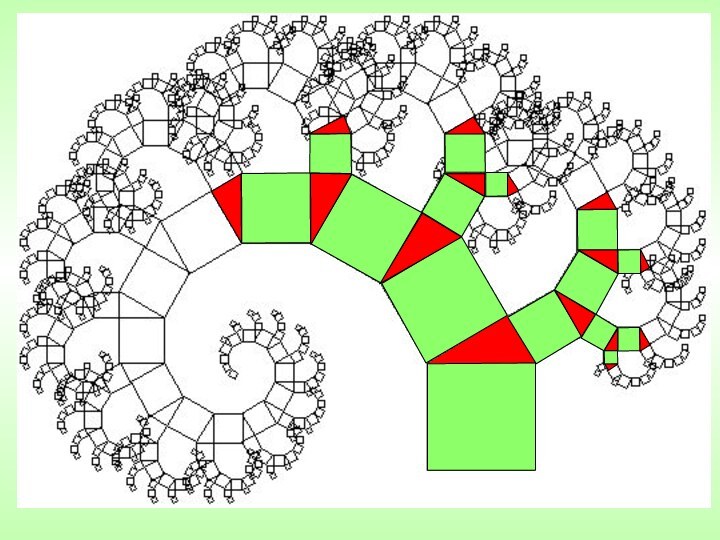
с математическим обоснованием графической интерпретации фрактальных образов
МЕТОДЫ ИЗУЧЕНИЯ
Анализ литературы

по теме исследования,
Изучение фракталов различного вида,
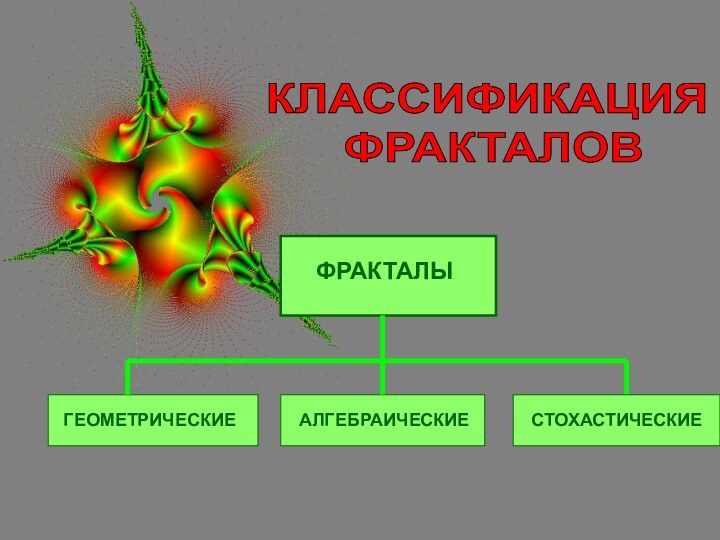
Разработать классификацию фракталов,
Собрать коллекцию фрактальных образов.

Фракталы в природе

которые могут быть поделены на части, каждая из которых

будет представлять уменьшенную копию целого.
Fractal от латинского слова fractus, означает разбитый (поделенный на части).
Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.

ПОНЯТИЕ
ФРАКТАЛА

за недифференцируемость в каждой точке.

Геометрические фракталы являются также

самыми наглядными, т.к. сразу видна самоподобность.

Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.

ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ

Серпинского

формулы.

Получают их с помощью нелинейных процессов в n–мерных пространствах.

Самыми

известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона

АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ

итераций комплексной функции

может быть сделано, пока точка z не

выйдет за пределы круга радиуса r 


Здесь z — комплексное число, соответствующее точке .

Множество Жюлиа — это множество таких точек, что отображения вида

не отображают их в окрестность бесконечности. На рисунке эти точки окрашены лиловым цветом.
Картинка получена выбором параметров a = 1.8, и b = 0.2 i и поворотом на 900

помощью той же процедуры, что и выше. Различие состоит

в том, что начальное значение для точки z берётся всегда равным нулю, а точке с координатами (х; у) на картинке соответствует комплексный параметр b = x + y i.

любого натурального числа n, то получим многочисленный класс фрактальных

множеств высокой симметрии, порядок которой определяется натуральной степенью. Для составления программы Fractal5, которая вычисляет каждую итерацию по формуле f(z)=zn+c, где с=a+ib, пришлось использовать тригонометрическую форму задания комплексного числа

Фракталы множеств комплексных степеней.

п = 9

итеративной системе случайным образом изменяются какие-либо параметры.

Эти фракталы используются

при моделировании рельефов местности и поверхности морей, процесса электролиза.

Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.

СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ