Презентация на тему Задачи оптимизации

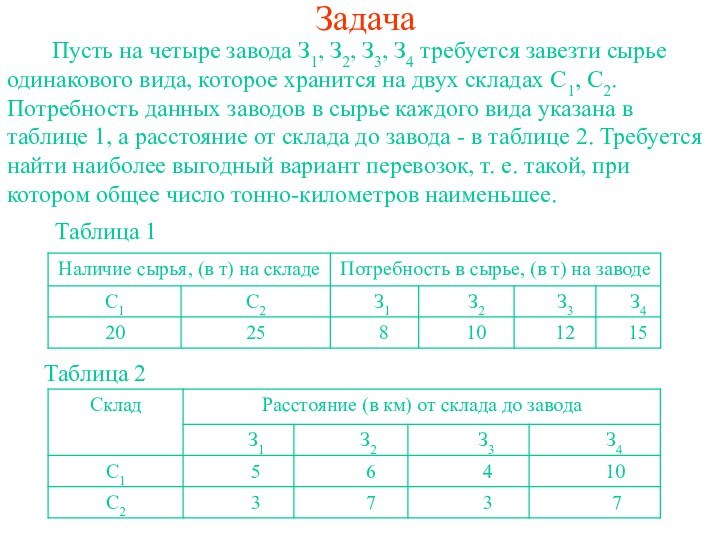
завода З1, З2, З3, З4 требуется завезти сырье одинакового

вида, которое хранится на двух складах С1, С2. Потребность данных заводов в сырье каждого вида указана в таблице 1, а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок, т. е. такой, при котором общее число тонно-километров наименьшее.

Таблица 1

Таблица 2

задачи, в первую очередь, проанализируем ее условие и переведем

его на язык математики, т. е. составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y и z соответственно. Тогда на четвертый завод с этого склада нужно будет перевезти 20 - x – y - z сырья в тоннах, а со второго склада нужно будет перевезти соответственно 8 - x, 10 - y, 12 - z, x + y + z - 5 сырья в тоннах. Запишем эти данные в таблицу 3.

Таблица 3

величины, входящие в эту таблицу, должны быть неотрицательными, получим

следующую систему неравенств

Эта система неравенств определяет многогранник M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12).

6y + 4z + 10(20 - x - y

- z) + 3(8 - x) + 7(10 - y) + 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.
Таким образом, задача сводится к отысканию наименьшего значения функции F = 295 - x - 4y - 2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.

Для нахождения наибольшего значения линейной функции на многограннике, достаточно вычислить значения функции в вершинах многогранника и выбрать из них наибольшее. Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограниче­ний: f(M1) = 52, f(M2) = 60, f(M3) = 56, f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24. Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точке M2(0,10,10).

4.
Таблица 4
Заметим, что число независимых переменных в этой задаче

было равно трем и поэтому в процессе ее решения получился многогранник. Если бы число независимых переменных равнялось двум, то получился бы многоугольник. В реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются электронно-вычислительные машины.

является графиком линейной функции z = ax + by

+ c?

Ответ: Плоскость.

график линейной функции z = ax + c по

отношению к оси Oy?

Ответ: Параллелен.

график линейной функции z = ax + by по

отношению к началу координат?

Ответ: Проходит через начало координат.

с графиком линейной функции z = ax + by

+ c, если c: а) увеличить на единицу; б) уменьшить на единицу?

Ответ: а) Поднимется на единицу;

б) опустится на единицу.

модель некоторой задачи представляется следующей системой ограничений
Ответ: -2.

На множестве решений этой системы найдите наименьшее значение функции F = y - x.

складах хранится сырье одинакового вида в количествах соответственно 10

т, 20 т, 30 т. На завод нужно завезти 35 т сырья. Найдите наиболее выгодный вариант перевозок, если расстояния от складов до завода равны 7 км, 5 км, 8 км.

Ответ: С 1-го склада – 10 т, со 2-го – 20 т, с 3-го – 5 т.

задачу при дополнительном требовании: со второго склада вывозится сырья

не больше, чем с третьего.

Ответ: С 1-го склада – 0 т, со 2-го и 3-го – 17,5 т.