- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи по многогранникам
Содержание
- 2. Параллелепипед – поверхность, составленная из шести параллелограммов.
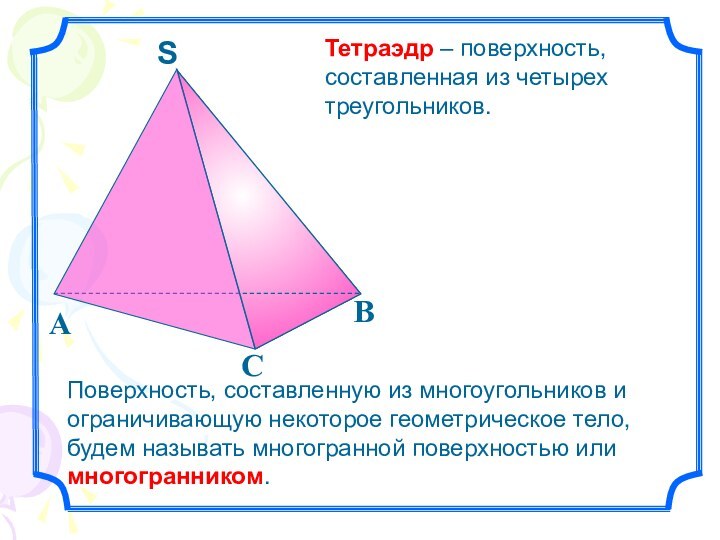
- 3. Тетраэдр – поверхность, составленная из четырех треугольников.
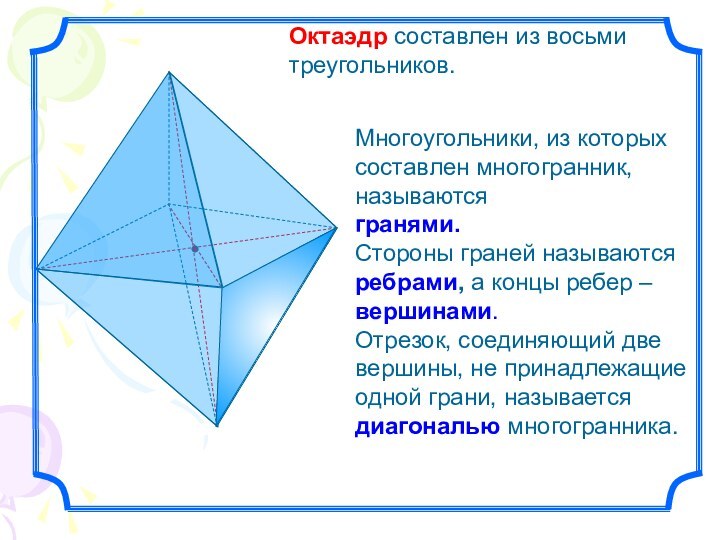
- 4. Октаэдр составлен из восьми треугольников.Многоугольники, из которых
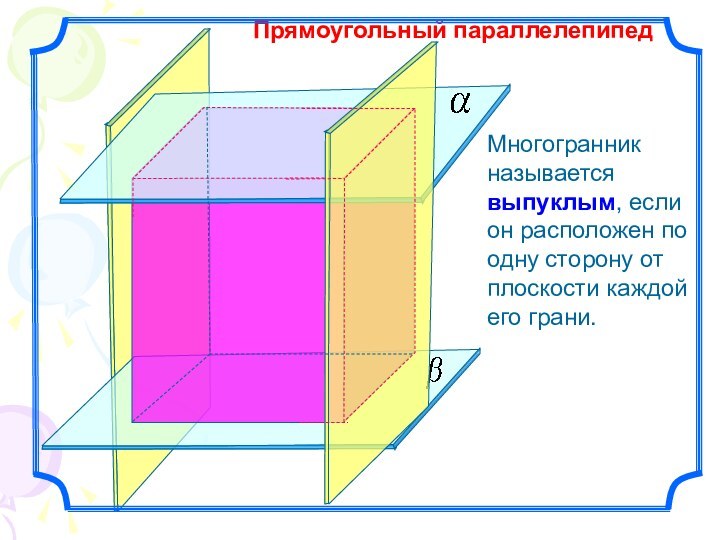
- 5. Прямоугольный параллелепипедМногогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
- 6. Невыпуклый многогранник
- 7. ПризмаА1А2АnB1B2BnB3А3Многогранник, составленный из двух равных многоугольников А1А2…Аn
- 8. ПризмаА1А2АnB1B2BnB3А3Отрезки А1В1, А2В2 и т.д. - боковые
- 9. Если боковые ребра перпендикулярны к основаниям, то
- 10. Прямая призма называется правильной, если ее основания
- 11. Площадью полной поверхности призмы называется сумма площадей
- 15. 1. Сторона основания правильной треугольной призмы равна
- 17. D Высота правильной четырехугольной призмы
- 23. АB C1B1А1 C
- 24. 1200А1
- 26. АB 24 C1B1А1 C 3512
- 27. Dd
- 30. АВСС1В1А12D
- 31. Скачать презентацию
- 32. Похожие презентации




















Слайд 4
Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен
многогранник, называются
гранями.
Стороны граней называются ребрами, а концы ребер
– вершинами.Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 5
Прямоугольный параллелепипед
Многогранник называется выпуклым, если он расположен по
одну сторону от плоскости каждой его грани.
Слайд 7
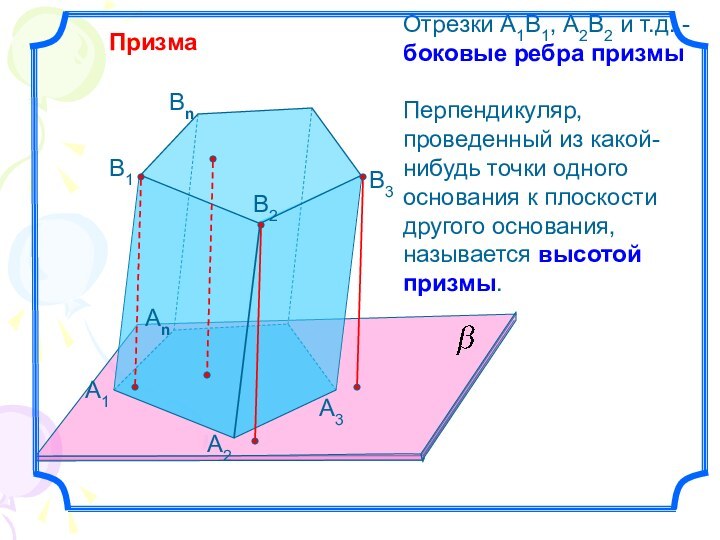
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и
В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется
призмой.n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn –
основания призмы.
Параллелограммы
А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
Слайд 8
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра
призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости
другого основания, называется высотой призмы.Слайд 9 Если боковые ребра перпендикулярны к основаниям, то призма
называется прямой, в противном случае наклонной.
Высота прямой призмы равна
ее боковому ребру.Слайд 10 Прямая призма называется правильной, если ее основания -
правильные многоугольники. У такой призмы все боковые грани –
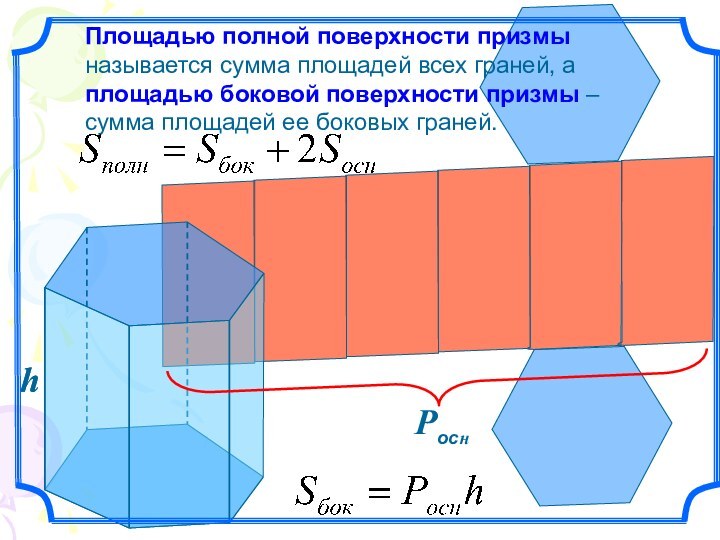
равные прямоугольники.Слайд 11 Площадью полной поверхности призмы называется сумма площадей всех
граней, а площадью боковой поверхности призмы – сумма площадей
ее боковых граней.h
h
Pocн
Слайд 12
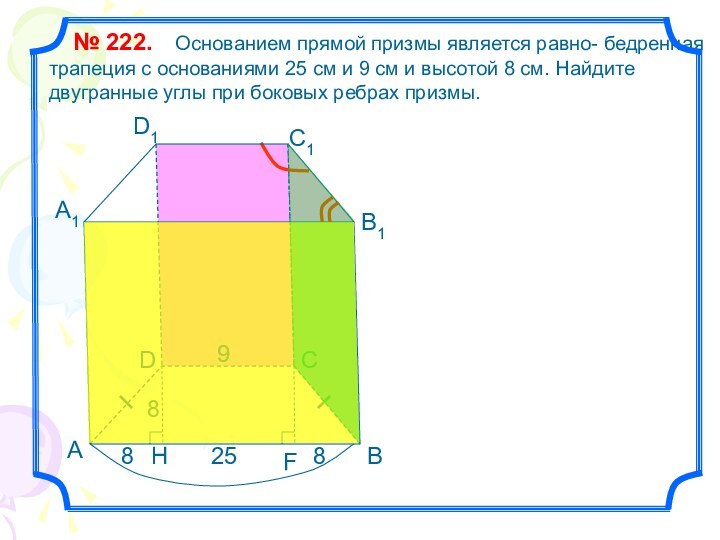
Основанием прямой призмы является равно- бедренная трапеция
с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.№ 222.
25
9
8
H
В
С
D
А1
D1
С1
В1
А
9
Слайд 13
В прямоугольном параллелепипеде стороны основания равны 12 см
и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.№ 219.
В
С
А1
D1
С1
В1
?
D
А
12 см
5 см
Слайд 14
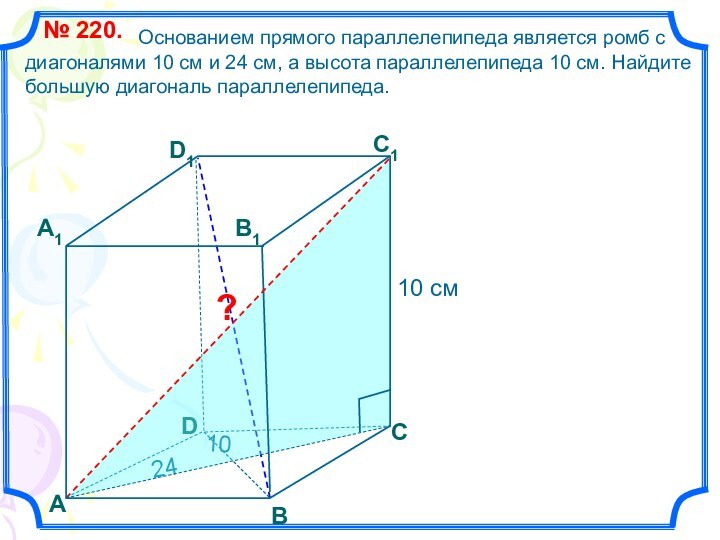
Основанием прямого параллелепипеда является ромб с диагоналями 10
см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.№ 220.
В
С
А1
D1
С1
В1
?
D
А
24
10
10 см
Слайд 15 1. Сторона основания правильной треугольной призмы равна 8
см, а диагональ боковой грани равна 10 см. Найдите
площадь боковой и полной поверхности призмы.2. Основание прямой призмы – параллелограмм со сторонами 8 и 15 см и углом 120о. Боковая поверхность призмы имеет площадь 460 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с катетами 13 и 12 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Слайд 16
Сторона основания правильной треугольной призмы
равна
8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.№ 221.
А
В
С
С1
В1
А1
8
6
8
8
8
10
Слайд 17
D
Высота правильной четырехугольной призмы равна
, а сторона основания – 8
см. Найдите расстояние между вершиной А и точкой пересечения диагоналей грани DD1С1С.С1
В1
А1
D1
С
В
А
О
8
8
Слайд 18
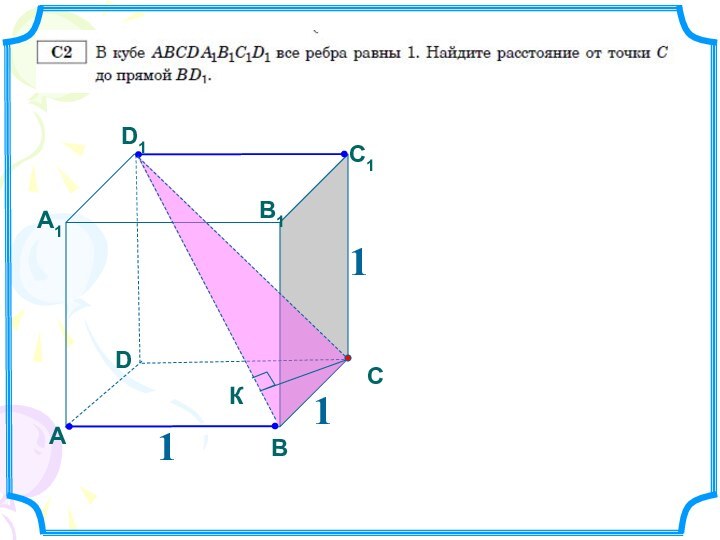
Через два противолежащих ребра проведено сечение,
площадь которого равна см2. Найдите ребро куба и егодиагональ.
№ 223.
D
А
В
С
А1
D1
С1
В1
a
a
a
S=
Слайд 19
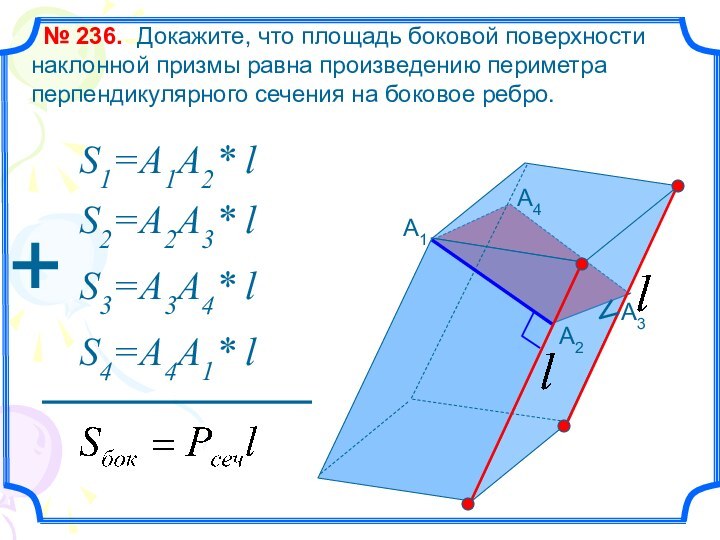
Докажите, что площадь боковой поверхности наклонной призмы равна произведению
периметра перпендикулярного сечения на боковое ребро.№ 236.
A3
A4
S1=A1A2* l
S2=A2A3* l
S3=A3A4* l
S4=A4A1* l
Слайд 20
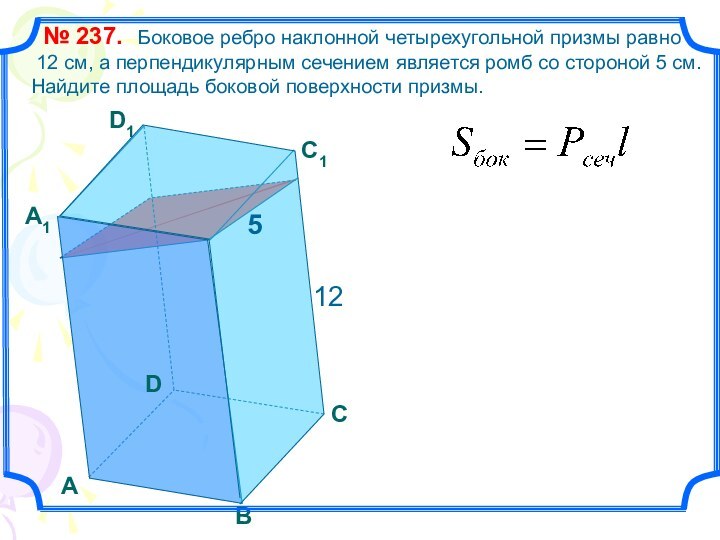
Боковое ребро наклонной четырехугольной призмы равно
12 см, а
перпендикулярным сечением является ромб со стороной 5 см. Найдите площадь боковой поверхности призмы.№ 237.
А
В
С
D
А1
D1
С1
12
5
Слайд 21
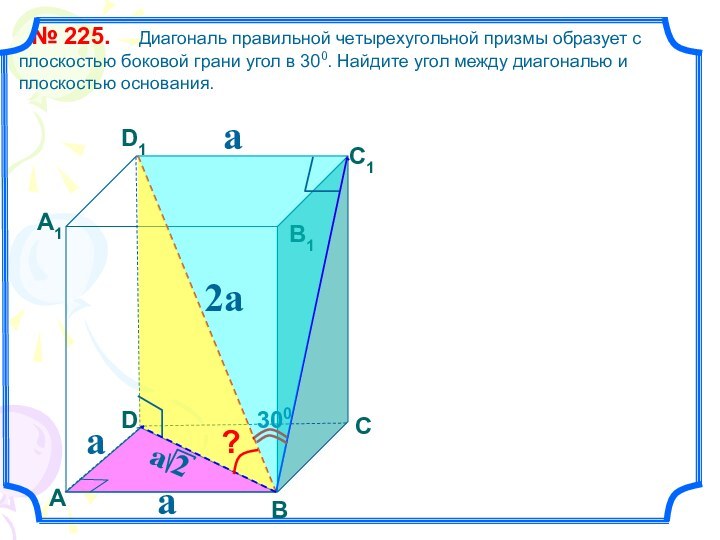
Диагональ правильной четырехугольной призмы образует с плоскостью боковой
грани угол в 300. Найдите угол между диагональю и плоскостью основания.№ 225.
В
С
А1
D1
С1
В1
D
А
a
2a
Слайд 22
В правильной четырехугольной призме через диагональ основания проведено сечение
параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2 см, а ее высота 4 см. № 226.
D
А
В
С
D1
С1
В1
А1
2
2
4
O
N
Слайд 23
А
B
C1
B1
А1
C
Основанием наклонной призмы
АВСА1В1С1 является равнобедренный треугольник АВС, в котором АС=АВ=13см, ВС=10см,а боковое ребро призмы образует с плоскостью основания угол в 450. Проекцией вершины А1 является точка пересечения медиан треугольника АВС. Найдите площадь грани СС1В1В.№ 228.
13
13
10
Слайд 24
1200
А1
Основание
прямой призмы – треугольник со сторонами 5 см и
3 см и углом в 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.№ 230.
А
В
С
С1
В1
3
5
S=35 см2
Слайд 25
Стороны основания прямого параллелепипеда равны 8 см и
15
см и образуют угол в 600. Меньшая из площадей диагональных сечений равна 130 см2. Найдите площадь поверхности параллелепипеда.№ 231.
В
С
А1
D1
С1
В1
D
8
15
600
S=130см2
А
Слайд 26
А
B
24
C1
B1
А1
C
35
12
В наклонной треугольной призме две
боковые грани взаимно перпендикулярны, а их общее ребро, отстоящее от двух других боковых ребер на 12 см и 35 см, равно 24 см. Найдите площадь боковой поверхности призмы.№ 238.
Слайд 27
D
d
Диагональ прямоугольного параллелепипеда, равная d, образует с
плоскостью основания угол , а с одной из боковых граней – угол . Найдите площадь боковой поверхности параллелепипеда.№ 232.
А1
В1
С1
D1
А
В
С
Слайд 28
Основание прямой призмы АВСА1В1С1 является прямоугольный треугольник АВС
с прямым углом В. Через ребро ВВ1 проведено сечение ВВ1D1D, перпендикулярное кплоскости грани АА1С1С.
Найдите площадь сечения,
если АА1=10см, АD=27см,
DC= 12см.
№ 233.
А
С
В
В1
А1
С1
10
27
12
Sсеч = 10 * 18
Слайд 29
Основанием прямой призмы является прямоугольный треугольник. Через середину
гипотенузы перпендикулярно к ней проведена плоскость. Найдите Sсеч , если катеты равны 20см и 21см,а боковое ребро равно 42 см.
№ 234.
А
С
В
В1
А1
С1
42
20
21