- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Замечательные кривые
Содержание
- 2. Оглавление:ВведениеВыбор темы. Замечательные кривые Конус. Конические сеченияЭллипсГиперболаПараболаСпираль АрхимедаСинусоидаЦиклоидыГипоциклоидыКардиоида и улитка Паскаля
- 3. Введение Актуальность темы заключается в демонстрации применения
- 4. Выбор темы. Замечательные кривые. Я хочу познакомить
- 5. Все замечательные кривые - эллипс, гипербола и
- 6. ЭЛЛИПСПРАКТИКА: Возьмите плотный лист бумаги, прикрепите
- 7. ГИПЕРБОЛАПРАКТИКА: Используя определение гиперболы, нетрудно изготовить простейший
- 8. ПАРАБОЛА ПРАКТИКА: Парабола – одно из конических
- 9. СПИРАЛЬ АРХИМЕДАПРАКТИКА: Пусть по радиусу равномерно
- 10. СИНУСОИДАПРАКТИКА: Сделайте из плотной бумаги, свернув ее
- 11. ЦИКЛОИДАПРАКТИКА: Представьте, что по прямой линии
- 12. ГИПОЦИКЛОИДЫ ПРАКТИКА:Возьмите кусок толстого картона и
- 13. КАРДИОИДА и УЛИТКА ПАСКАЛЯТЕОРИЯ: Понаблюдаем за
- 14. Скачать презентацию
- 15. Похожие презентации











Слайд 2
Оглавление:
Введение
Выбор темы. Замечательные кривые
Конус. Конические сечения
Эллипс
Гипербола
Парабола
Спираль Архимеда
Синусоида
Циклоиды
Гипоциклоиды
Кардиоида
и улитка Паскаля
Слайд 3
Введение
Актуальность темы заключается в демонстрации применения математических знаний
в практической деятельности человека. В школьном курсе математики не
изучаются свойства замечательных кривых, которые широко используются в жизни.Гипотеза: Использование данного материала на уроках математики расширяет кругозор учащихся по кривым, изучаемым по школьной программе – окружность, парабола и гипербола, и показывает их практическое применение в жизни.
Цель данной работы: Составить компьютерную презентацию для применения на уроках математики по свойствам замечательных кривых.
Задачи: В помощь учителю. Используя минимум времени, принести максимум пользы.
Практическая значимость работы: Я считаю, что моя работа пригодится учителям доступно и красочно продемонстрировать учащимся практическое применение свойств замечательных кривых, научить строить кривые при помощи несложных школьных инструментов.
Слайд 4
Выбор темы.
Замечательные кривые.
Я хочу познакомить вас с некоторыми
поистине замечательными кривыми, населяющими удивительный мир геометрии, которые встречаются
в нашей жизни гораздо чаще, чем кажется. Они не так уж редки в природе, имеют практическое приложение в жизни человека. Знание их замечательных свойств используется в различных механизмах, применяемых человеком в жизни.Я выбрала эту тему, так как считаю её, интересной и содержательной, развивающей познавательный интерес к урокам математики, открывающей практическое приложение математики в жизни. Использование данного материала на уроках математики расширяет кругозор учащихся по кривым, изучаемым по школьной программе. В школьном курсе математики рассматриваются кривые – гипербола, парабола, синусоида, окружность. Но ни где не говорится о замечательных свойствах данных кривых, а тем более об их практическом применении. Я считаю, что очень важно учащимся знать замечательные свойства данных кривых, которые широко применяются в жизни. Изучая и даже просто знакомясь с этими свойствами, учащиеся видят действительно практическое применение математики. А эллипс нужно обязательно ввести в курс математики, так как это отправная тема в изучении кривых, которая расширяется и теоретически обосновывается уже в 11 классе при изучении темы «Конус».
Для этого я познакомилась с материалом о замечательных кривых и их свойствах в различных пособиях и энциклопедиях по математике.
Мои исследования.
Я считаю, что составила компьютерное приложение к урокам математики. В данной работе собран материал с уклоном на практическое построение кривых, большое внимание уделяется применению свойств кривых в жизни. В своей работе изучение каждой кривой я рассмотрела в трёх направлениях:
Практика – как построить ученику данную кривую при помощи школьных инструментов,
Теория – определение кривой и его замечательного свойства,
Приложение – практическое применение данной кривой в жизни человека.
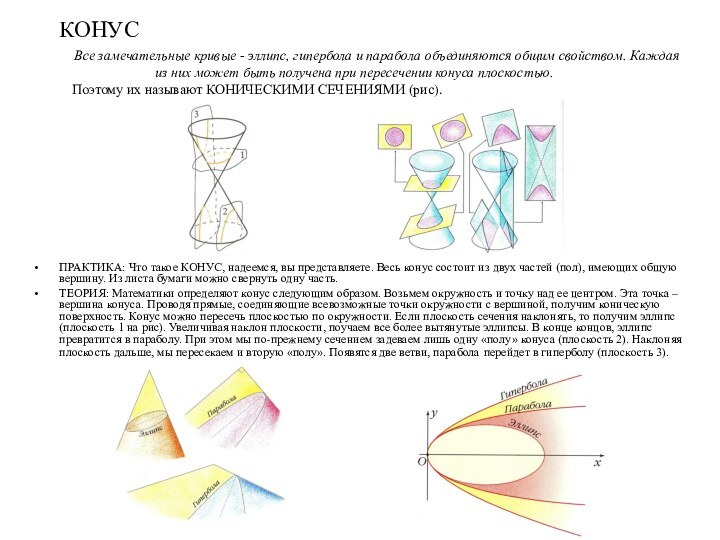
Слайд 5 Все замечательные кривые - эллипс, гипербола и парабола
объединяются общим свойством. Каждая из них может быть получена
при пересечении конуса плоскостью.Поэтому их называют КОНИЧЕСКИМИ СЕЧЕНИЯМИ (рис).
КОНУС
ПРАКТИКА: Что такое КОНУС, надеемся, вы представляете. Весь конус состоит из двух частей (пол), имеющих общую вершину. Из листа бумаги можно свернуть одну часть.
ТЕОРИЯ: Математики определяют конус следующим образом. Возьмем окружность и точку над ее центром. Эта точка – вершина конуса. Проводя прямые, соединяющие всевозможные точки окружности с вершиной, получим коническую поверхность. Конус можно пересечь плоскостью по окружности. Если плоскость сечения наклонять, то получим эллипс (плоскость 1 на рис). Увеличивая наклон плоскости, поучаем все более вытянутые эллипсы. В конце концов, эллипс превратится в параболу. При этом мы по-прежнему сечением задеваем лишь одну «полу» конуса (плоскость 2). Наклоняя плоскость дальше, мы пересекаем и вторую «полу». Появятся две ветви, парабола перейдет в гиперболу (плоскость 3).
Слайд 6
ЭЛЛИПС
ПРАКТИКА: Возьмите плотный лист бумаги, прикрепите к
нему в двух точках нитку и натяните карандашом эту
нитку. Нарисуйте линию, двигая карандаш и натягивая нитку, получите эллипс.ПРИЛОЖЕНИЕ: На самом деле эллипсы в нашей жизни встречаются гораздо чаще, чем кажется. Например, когда мы режем наискосок колбасу, то получающееся сечение имеет эллиптическую форму. Планеты движутся вокруг Солнца по эллиптическим орбитам, причем Солнце находится в одном из фокусов. О свойствах эллипсов во всех подробностях могут рассказать специалисты, изучающие движение небесных тел. Согласно закону, открытому в начале XVII в. немецким астрономом Иоганном Кеплером, все планеты движутся вокруг Солнца по орбитам, имеющим форму эллипса.
У эллипса есть целый ряд свойств, которые могут иметь самые неожиданные применения. Так, если мы сделаем зеркало в форме эллипса и поместим в одном из фокусов источник света, то лучи, отразившись от зеркала, соберутся в другом фокусе. У эллипса есть замечательное оптическое свойство: прямые, соединяющие любую его точку с фокусами, составляют с касательной к эллипсу в этой точке равные углы. Если представить себе, что эллипс, подобно зеркалу, может отражать световые лучи, и поместить в один из его фокусов источник света, то лучи, отражаясь от эллипса, соберутся в другом его фокусе (рис).
Так же распространяются и акустические волны, что используют архитекторы для создания поразительных звуковых эффектов: «говорящих» бюстов, «магического» шёпота, «потусторонних» звуков (рис). Это свойство лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружений, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико (рис).
ТЕОРИЯ: Эта линия называется ЭЛЛИПСОМ. Все точки эллипса, как видно из построения, обладают одним свойством: Сумма расстояний от них до двух заданных точек плоскости (эти точки называются ФОКУСАМИ эллипса) постоянна. Окружность – частный случай эллипса, она получается, если фокусы эллипса совпадают.
Слайд 7
ГИПЕРБОЛА
ПРАКТИКА: Используя определение гиперболы, нетрудно изготовить простейший прибор
для её вычерчивания. Нужно взять линейку, нить и три
кнопки. Две кнопки воткнуть в лист бумаги (рис) – и в этих точках будут фокусы гиперболы – и к ним привязать концы нити. Третью кнопку втыкают в линейку около её края, привязав к ней нить недалеко от середины нити, но не в середине. Если теперь, прижимая нить к краю линейки кончиком карандаша и держа нить всё время в натянутом состоянии, двигать карандаш, то её графит будет вычерчивать на бумаге одну из ветвей гиперболы. Заметим, что если нить привязать к третьей кнопке ровно в середине нити то гипербола вырождается в прямую – срединный перпендикуляр отрезка F1F2.ТЕОРИЯ: Для этой кривой мы не можем предложить, как в предыдущем случае, достаточно простой «гиперболический циркуль», позволяющий вычерчивать гиперболу и одновременно показывающий ее основное свойство. Поэтому начнем с указания основного свойства, задающего гиперболу.
Гипербола – эта линия, для всех точек, которой разность расстояний до двух заданных точек плоскости (фокусов гиперболы) есть величина постоянная (рис).
Гипербола состоит из двух частей (двух отдельных ветвей). Все точки одной ветви ближе к одному фокусу (соответствующим образом берется и разность расстояний), а другой ветви к другому.
Ещё пример – зона слышимости звука пролетающего самолёта. Если самолёт движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует конус (рис). Поверхность Земли может приближённо считаться плоскостью, рассекающей этот конус.
ПРИЛОЖЕНИЕ:
Гипербола, как и другие конические сечения, обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса (рис).
Если сделать зеркало изогнув зеркально отполированный лист металла по дуге гиперболы, а на прямой, соответствующей фокусу гиперболы, поместить свечу (рис, то наблюдатель, находящийся по ту сторону от зеркала, что и свеча, увидит её отражение как бы в одном и том же месте, точно так же, как и при отражении от плоского зеркала (вспомним, что прямая является частным случаем гиперболы, и соответствующее зеркало будет плоским).
Слайд 8
ПАРАБОЛА
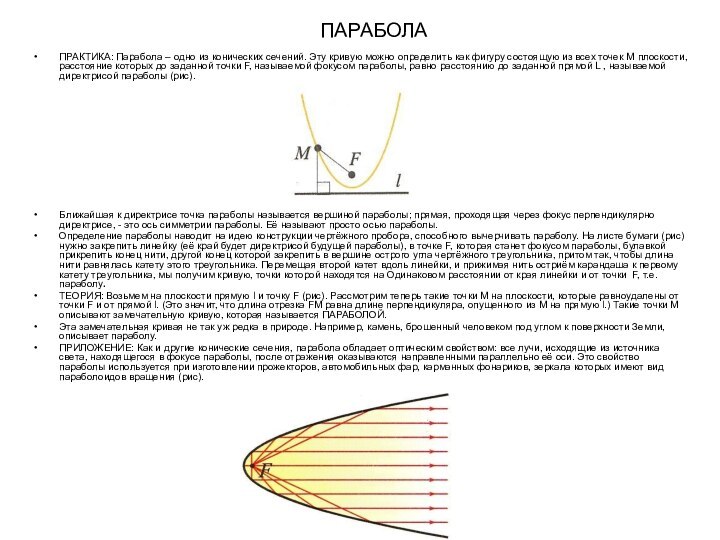
ПРАКТИКА: Парабола – одно из конических сечений. Эту
кривую можно определить как фигуру состоящую из всех точек
М плоскости, расстояние которых до заданной точки F, называемой фокусом параболы, равно расстоянию до заданной прямой L , называемой директрисой параболы (рис).Ближайшая к директрисе точка параболы называется вершиной параболы; прямая, проходящая через фокус перпендикулярно директрисе, - это ось симметрии параболы. Её называют просто осью параболы.
Определение параболы наводит на идею конструкции чертёжного пробора, способного вычерчивать параболу. На листе бумаги (рис) нужно закрепить линейку (её край будет директрисой будущей параболы), в точке F, которая станет фокусом параболы, булавкой прикрепить конец нити, другой конец которой закрепить в вершине острого угла чертёжного треугольника, притом так, чтобы длина нити равнялась катету этого треугольника. Перемещая второй катет вдоль линейки, и прижимая нить остриём карандаша к первому катету треугольника, мы получим кривую, точки которой находятся на Одинаковом расстоянии от края линейки и от точки F, т.е. параболу.
ТЕОРИЯ: Возьмем на плоскости прямую l и точку F (рис). Рассмотрим теперь такие точки М на плоскости, которые равноудалены от точки F и от прямой l. (Это значит, что длина отрезка FM равна длине перпендикуляра, опущенного из M на прямую l.) Такие точки М описывают замечательную кривую, которая называется ПАРАБОЛОЙ.
Эта замечательная кривая не так уж редка в природе. Например, камень, брошенный человеком под углом к поверхности Земли, описывает параболу.
ПРИЛОЖЕНИЕ: Как и другие конические сечения, парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (рис).
Слайд 9
СПИРАЛЬ АРХИМЕДА
ПРАКТИКА: Пусть по радиусу равномерно вращающегося
диска с постоянной скоростью ползет муравей. Проползая вперед, он
одновременно смещается в сторону вращения диска.ТЕОРИЯ: Таким образом, путь муравья представляет кривую (рис.). Она называется СПИРАЛЬЮ АРХИМЕДА (в переводе с латыни спираль означает «изгиб», «извив»). Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между витками; каждое из которых равно 2πα (рис).
ПРИЛОЖЕНИЕ: По спирали Архимеда идёт, например звуковая дорожка. Одна из деталей швейной машинки – механизм для равномерного наматывания нити на шпульку – имеет форму спирали Архимеда (рис).
Слайд 10
СИНУСОИДА
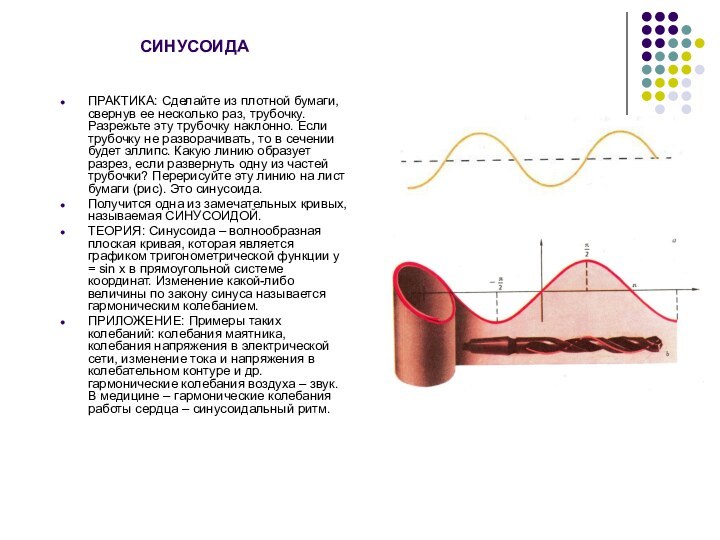
ПРАКТИКА: Сделайте из плотной бумаги, свернув ее несколько
раз, трубочку. Разрежьте эту трубочку наклонно. Если трубочку не
разворачивать, то в сечении будет эллипс. Какую линию образует разрез, если развернуть одну из частей трубочки? Перерисуйте эту линию на лист бумаги (рис). Это синусоида.Получится одна из замечательных кривых, называемая СИНУСОИДОЙ.
ТЕОРИЯ: Синусоида – волнообразная плоская кривая, которая является графиком тригонометрической функции y = sin x в прямоугольной системе координат. Изменение какой-либо величины по закону синуса называется гармоническим колебанием.
ПРИЛОЖЕНИЕ: Примеры таких колебаний: колебания маятника, колебания напряжения в электрической сети, изменение тока и напряжения в колебательном контуре и др. гармонические колебания воздуха – звук. В медицине – гармонические колебания работы сердца – синусоидальный ритм.
Слайд 11
ЦИКЛОИДА
ПРАКТИКА: Представьте, что по прямой линии без
скольжения катится круг. Проследите за траекторией, которую опишет при
этом точка А, взятая на окружности этого круга (рис. а). Начертите получившуюся кривую.ТЕОРИЯ: Она называется ЦИКЛОИДОЙ (рис.). Циклоида обладает многими замечательными свойствами. Вот одно из них. Давно математики пытались решить такую задачу: какой формы должен быть гладкий желоб, соединяющий две точки А и В (А выше, чем В), чтобы гладкий металлический шарик скатился по этому желобу из точки А в точку В под действием своего веса за кратчайшее время? Можно подумать, что желоб должен быть прямолинейным. Но это не так. Может быть, желоб следует выгнуть по дуге окружности, как думал великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже XVI-XVII вв.? Нет, Галилей ошибался. Только в 1696 г. швейцарский математик Иоганн Бернулли установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (рис. в).
ПРИЛОЖЕНИЕ: В связи с циклоидами расскажем об одном интересном парадоксе (слово «парадокс» означает неожиданное явление, не соответствующее обычным представлениям). Допустим, что пассажирский поезд едет из Москвы в Киев. Оказывается, в каждый момент времени в этом поезде, более того, в каждом вагоне есть точки, движущиеся в обратном направлении. Вы можете удивляться, но это так. Все дело в устройстве железнодорожных колес. Если смотреть вдоль рельс, то можно увидеть выступ на колесе (рис. г), который опускается ниже рельса. Роль этого выступа очень велика, он не позволяет колесам сойти с рельс. Так вот, самая нижняя часть колеса, находящаяся ниже его опорной точки, движется в направлении, обратном движению всего колеса.
Если выбрать крайнюю точку колеса, то линия, описываемая ею, будет выглядеть, как на рисунке д. Обратное движение это точка совершает в нижних частях маленьких петель.
Перевернём циклоиду выпуклостью вниз и представим, что по ней скатывается тяжёлая частица. Из какой бы точки циклоиды ни начинала движение частица, она скатится вниз за одно и то же время. Замечательное свойство изохронности (от греческого «изос» - «равный» и «хронос» - «время») циклоиды навело Христиана Гюйгенса, нидерландского математика, физика и механика (1629-1695) на мысль использовать её в часовом маятнике. Он предложил подвесить шарик на нити и ограничить свободу его перемещения доской, край которой имеет форму циклоиды (рис).
Оказывается, в таком случае движение шарика также происходит по циклоиде, и, следовательно, на период его колебаний не влияет отклонения шарика от вертикали, т.е. амплитуда колебаний. В 1696 году Даниил Бернулли (1700-1782) швейцарский учёный открыл другое замечательное свойство этой кривой. По циклоиде при отсутствии трения частица под действием силы тяжести скатывается из заданной точки в другую за наименьшее время. Это кривая наибыстрейшего спуска. Иначе говоря, скатываясь по снежной горке, профиль которой выполнен в виде циклоиды, мы окажемся у основания горки быстрее, чем в случае другой формы горки.
Слайд 12
ГИПОЦИКЛОИДЫ
ПРАКТИКА:Возьмите кусок толстого картона и вырежьте
в нем круг радиусом 12 см. Из того же
материала вырежьте три круга радиусами 4 см, 3 см и 2 см. Положите кусок картона с вырезанным в нем отверстием на лист бумаги, вложите в этот вырез первый из трех кружков, чтобы он касался края, и отметьте на окружности маленького круга точку (рис. а). Проследите за тем, какую линию опишет отмеченная точка, когда кружок катится по окружности выреза без скольжения. Проделайте то же самое со вторым и третьим кругами.ТЕОРИЯ: Получившиеся линии – ГИПОЦИКЛОИДЫ (рис.б). Все кривые, которые вычерчивает точка на окружности, катящейся внутри другой окружности, принадлежит семейству гипоциклоид (от греческого «гипо» - «под», «внизу» и «киклоидес» - «кругообразный»).
ЗАДАНИЕ НА САМОСТОЯТЕЛЬНОЕ РЕШЕНИЕ: о что превратится гипоциклоида, если радиус меньшего круга равен 6 см, а большего – 12 см? Как выглядит гипоциклоида для кругов с радиусом 8 см, 9 см и 10 см?
Слайд 13
КАРДИОИДА и УЛИТКА ПАСКАЛЯ
ТЕОРИЯ: Понаблюдаем за какой-нибудь
точкой окружности, когда последняя катится по внешней стороне неподвижной
окружности равного радиуса. Траекторией точки будет КАРДИОИДА.КАРДИОИДА. Такое название она получила из-за сходства с сердцем (греческое слово «кардио» означает «сердце»). Если, точку, описывающую кривую, взять не на самой окружности, а несколько сбоку, то получим кривую, называемую улиткой Паскаля.
ПРАКТИКА: Вырежьте два одинаковых картонных круга. Один из них закрепите неподвижно. Второй приложите к первому, отметьте на его краю точку А, наиболее удаленную от центра первого круга (рис. а). Прокатите без скольжения подвижный круг по неподвижному, и понаблюдайте, какую линию опишет точка А. Начертите эту линию.
ПРИЛОЖЕНИЕ: Улитка Паскаля применяется для вычерчивания профиля эксцентрика, если требуется, чтобы скользящий по профилю стержень совершал гармонические колебания (рис). Такие механизмы отличаются плавностью возвратно-поступательного движения стержня ( например, в механике автомашин).