Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Знакомьтесь, уравнение

Содержание

Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья
Карл Фридрих Гаусс (1777-1855) немецкий математик, астроном, геодезист и физик, иностранный член-корреспондент Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья Определение квадратного уравненияназывается квадратным уравнением где х – переменная, а, b МОУ Тулиновская средняя общеобразовательная школаназывается дискриминантомВыражение МОУ Тулиновская средняя общеобразовательная школаaх2 + вх + с = 0, а≠0D Исторические сведенияНеобходимость решать уравнения не только первой, но и второй степени в Цель исследования:Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейкиМОУ Тулиновская средняя общеобразовательная школа ГипотезаПо данным действительным коэффициентам a, b, c уравнения ax2 + bx + Ход исследования:1. Изучив теоретический материал учебника и дополнительных источников информации выяснить, способы Задача. По данным действительным коэффициентам a, b, Ход решения задачиух(х1;0) (х2;0)FBKEAOC(0;1) S(;)(0;)МОУ Тулиновская средняя общеобразовательная школа План нахождения корней квадратного уравнения с помощью циркуля и линейкиВ системе координат ух(х1;0)KEAO(0;1) S(0;)Радиус окружности больше ординаты центраВ этом случае окружность пересекает ось Ох ух(х1;0)EAO(0;1) S(0;)Радиус окружности равен ординате центраВ этом случае уравнение имеет равные действительные ухEAO(0;1) S(0;)Радиус окружности меньше ординаты центраВ этом случае окружность не имеет общих Примеры:а) 2x2 + 3x + 1 = 0Определим координаты точки центра Примеры:б) x2 - 5x + 6 = 0Определим координаты точки центра Выводы1. Квадратные уравнения можно решать с помощью циркуля и линейки.2. По данным Способы решения квадратных уравненийИзучаемые в школе: Разложение левой части на множители Метод Способы решения квадратных уравненийПродвинутые способы: Способ переброски По свойству коэффициентов С помощью Глейзер Г.И. История математики в школе. – М., Просвещение, 1982. Лиман
Слайды презентации

Слайд 2 Знакомьтесь, уравнение!
Работу выполнила
ученица 9-го класса
Лёвина Дарья

Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья

Слайд 3 Определение квадратного уравнения
называется квадратным уравнением
где х –

Определение квадратного уравненияназывается квадратным уравнением где х – переменная, а, b

переменная,
а, b и c – некоторые числа,


причем а  0

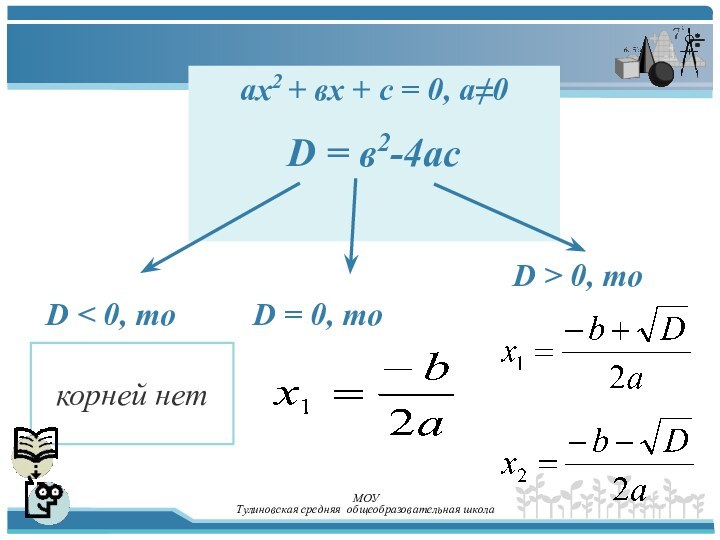
Уравнение вида

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 4 МОУ
Тулиновская средняя общеобразовательная школа
называется дискриминантом
Выражение

МОУ Тулиновская средняя общеобразовательная школаназывается дискриминантомВыражение

Слайд 5 МОУ
Тулиновская средняя общеобразовательная школа
aх2 + вх +

МОУ Тулиновская средняя общеобразовательная школаaх2 + вх + с = 0,

с = 0, а≠0
D = в2-4ас

D < 0, то
D

= 0, то

D > 0, то

корней нет

Слайд 6 Исторические сведения
Необходимость решать уравнения не только первой, но

Исторические сведенияНеобходимость решать уравнения не только первой, но и второй степени

и второй степени в древности была вызвана потребностью решать

задачи, связанные с нахождением площадей земельных участков и работами военного характера, с развитием астрономии и математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Web - сайт

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 7 Цель исследования:
Выяснить, можно ли решать квадратное уравнение с

Цель исследования:Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейкиМОУ Тулиновская средняя общеобразовательная школа

помощью циркуля и линейки
МОУ
Тулиновская средняя общеобразовательная школа

Слайд 8 Гипотеза
По данным действительным коэффициентам a, b, c уравнения

ГипотезаПо данным действительным коэффициентам a, b, c уравнения ax2 + bx

ax2 + bx + c = 0 (a ≠

0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 9 Ход исследования:
1. Изучив теоретический материал учебника и дополнительных

Ход исследования:1. Изучив теоретический материал учебника и дополнительных источников информации выяснить,

источников информации выяснить, способы решения квадратных уравнений с помощью

циркуля и линейки.
2. Изучить историю квадратных уравнений.
3. Оформить результаты, сделать соответствующие выводы.

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 10 Задача.
По данным

Задача. По данным действительным коэффициентам a, b, c уравнения

действительным коэффициентам a, b, c уравнения
ax2 + bx

+ c = 0 (a ≠ 0) определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения .

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 11 Ход решения задачи
у
х
(х1;0)
(х2;0)
F
B
K
E
A
O
C
(0;1)
S
(
;
)
(0;
)
МОУ
Тулиновская средняя общеобразовательная

Ход решения задачиух(х1;0) (х2;0)FBKEAOC(0;1) S(;)(0;)МОУ Тулиновская средняя общеобразовательная школа

школа

Слайд 12 План нахождения корней квадратного уравнения с помощью циркуля

План нахождения корней квадратного уравнения с помощью циркуля и линейкиВ системе

и линейки
В системе координат построим

точки

и А (0;1).
Проведём окружность с радиусом SA.
3. Абсциссы точек пересечения окружности с осью Ох являются корнями исходного квадратного уравнения.

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 13 у
х
(х1;0)
K
E
A
O
(0;1)
S
(0;
)
Радиус окружности больше ординаты центра
В этом случае

ух(х1;0)KEAO(0;1) S(0;)Радиус окружности больше ординаты центраВ этом случае окружность пересекает ось

окружность пересекает ось Ох в точках В(х1;0)

С(х2;0)

(х2;0)

С

В

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 14 у
х
(х1;0)
E
A
O
(0;1)
S
(0;
)
Радиус окружности равен ординате центра
В этом случае

ух(х1;0)EAO(0;1) S(0;)Радиус окружности равен ординате центраВ этом случае уравнение имеет равные

уравнение имеет равные действительные корни, абсцисса точки касания

х1,2 =

В

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 15 у
х
E
A
O
(0;1)
S
(0;
)
Радиус окружности меньше ординаты центра
В этом случае

ухEAO(0;1) S(0;)Радиус окружности меньше ординаты центраВ этом случае окружность не имеет

окружность не имеет общих точек с осью Ох и

уравнение имеет комплексные и сопряжённые корни х1,2 =
=

В

С

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 16 Примеры:
а) 2x2 + 3x + 1 =

Примеры:а) 2x2 + 3x + 1 = 0Определим координаты точки центра

0
Определим координаты точки центра окружности по формулам:
x =
y

=

Проведём окружность радиуса SA, где А(0;1). Корни уравнения -1 и - 0,5.

О

у

х

А

-0,5

S

-1

1

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 17 Примеры:
б) x2 - 5x + 6 =

Примеры:б) x2 - 5x + 6 = 0Определим координаты точки центра

0
Определим координаты точки центра окружности по формулам:
x =
y

=

Проведём окружность радиуса SA, где А(0;1). Корни уравнения 2 и 3.

О

у

х

А

3

1

2

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 18 Выводы
1. Квадратные уравнения можно решать с помощью циркуля

Выводы1. Квадратные уравнения можно решать с помощью циркуля и линейки.2. По

и линейки.
2. По данным действительным коэффициентам a, b, c

уравнения
ax2 + bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 19 Способы решения квадратных уравнений
Изучаемые в школе:
Разложение левой

Способы решения квадратных уравненийИзучаемые в школе: Разложение левой части на множители

части на множители
Метод выделения полного квадрата

С применением формул корней квадратного уравнения
С применением теоремы Виета
Графический способ

МОУ
Тулиновская средняя общеобразовательная школа

Слайд 20 Способы решения квадратных уравнений
Продвинутые способы:
Способ переброски
По

Способы решения квадратных уравненийПродвинутые способы: Способ переброски По свойству коэффициентов С

свойству коэффициентов
С помощью циркуля и линейки
С помощью

номограммы
Геометрический

МОУ
Тулиновская средняя общеобразовательная школа

  • Имя файла: znakomtes-uravnenie.pptx
  • Количество просмотров: 110
  • Количество скачиваний: 0
- Предыдущая История становления и развития духовной музыки
Следующая - Нарезка овощей

Похожие презентации

Презентация Запоминания таблиц умножения и рассмотрения каждой таблицы в отдельности презентация к уроку по математике (3 класс) Презентация Запоминания таблиц умножения и рассмотрения каждой таблицы в отдельности презентация к уроку по математике (3 класс) 124
Презентация Квадратный см презентация к уроку по математике (3 класс) Презентация Квадратный см презентация к уроку по математике (3 класс) 167
Презентация по ФЭМП презентация урока для интерактивной доски по математике (средняя группа) Презентация по ФЭМП презентация урока для интерактивной доски по математике (средняя группа) 133
Презентация по теме Простые и составные числа. Признаки делимости (Математика - 6 класс) Презентация по теме Простые и составные числа. Признаки делимости (Математика - 6 класс) 160
Математика сложение и вычитание Математика сложение и вычитание 144
Дидактическая игра Считаем устно Дидактическая игра Считаем устно 40
Свойства и признаки равнобедренного треугольника Свойства и признаки равнобедренного треугольника 103
triik 1 triik 1 111
Параллелограмм Вариньона Параллелограмм Вариньона 115
Презентация к уроку-обобщения по математике на тему Дроби Презентация к уроку-обобщения по математике на тему Дроби 107
ДРУЖОК. Правила по математике для начальных классов ДРУЖОК. Правила по математике для начальных классов 132
Внеклассное мероприятие Неделя математики на тему: Знай и умей Внеклассное мероприятие Неделя математики на тему: Знай и умей 119
Сложение двузначных чисел презентация к уроку по математике (2 класс) по теме Сложение двузначных чисел презентация к уроку по математике (2 класс) по теме 118
Великие женщины математики (6 класс) Великие женщины математики (6 класс) 154
Сценарий ООД в ДОУ для детей с ОВЗ (интеллектуальная недостаточность) презентация к уроку по математике (средняя группа) Сценарий ООД в ДОУ для детей с ОВЗ (интеллектуальная недостаточность) презентация к уроку по математике (средняя группа) 213
Математика Приемы умножения на два план-конспект урока по математике (2 класс) Математика Приемы умножения на два план-конспект урока по математике (2 класс) 45
Презентация по математике на тему:Прием устного умножения на двузначное число (4 класс) Презентация по математике на тему:Прием устного умножения на двузначное число (4 класс) 132
Системы счисления Системы счисления 96
Операции с многозначными числами Операции с многозначными числами 143
Порядок и хаос 5 класс Порядок и хаос 5 класс 131
Интерактивные игры для детей. Волшебный счет презентация урока для интерактивной доски по математике (средняя группа) Интерактивные игры для детей. Волшебный счет презентация урока для интерактивной доски по математике (средняя группа) 213
Обобщения опыта работы по теме:Математическое развитие дошкольников на занятиях и в свободной деятельности(младший возраст) материал по математике (младшая группа) Обобщения опыта работы по теме:Математическое развитие дошкольников на занятиях и в свободной деятельности(младший возраст) материал по математике (младшая группа) 98
Презентация Математика и физика в хокее Презентация Математика и физика в хокее 153
Наибольший общий делитель 6 класс Наибольший общий делитель 6 класс 120
Что изучает геометрия Что изучает геометрия 190
УСТНЫЕ ЗАДАНИЯ По теме натуральные числа УСТНЫЕ ЗАДАНИЯ По теме натуральные числа 116
Формы мышления. Алгебра высказываний Формы мышления. Алгебра высказываний 113
Решение неравенств второй степени с одной переменной Решение неравенств второй степени с одной переменной 105
Презентация к дипломной работе по теме Применение непрерывности функции к решению алгебрагических задач Презентация к дипломной работе по теме Применение непрерывности функции к решению алгебрагических задач 163
Граф. Построение графов Граф. Построение графов 86