- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
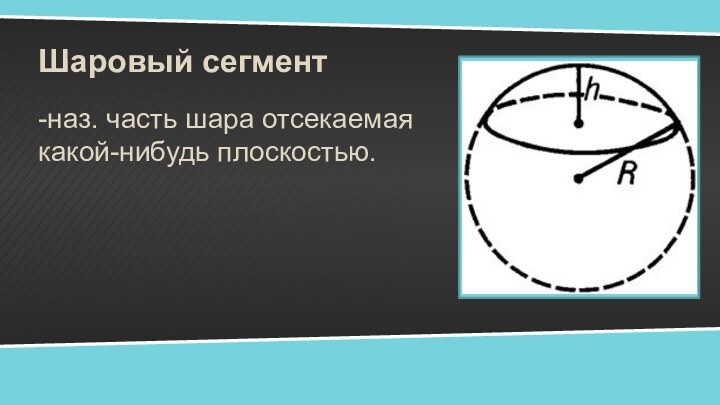
Презентация на тему Шаровый сегмент
Содержание
- 2. Шаровый сегмент вне шара
- 3. h- высота шарового сегментаr- радиус шарового сегментаo- основание сегментаrOЭлементы шарового сегмента
- 4. Формулы шарового сегментаобъем шарового сегмента вычисляется по
- 5. Шаровый сектор-наз. тело, полученное вращением кругового сектора
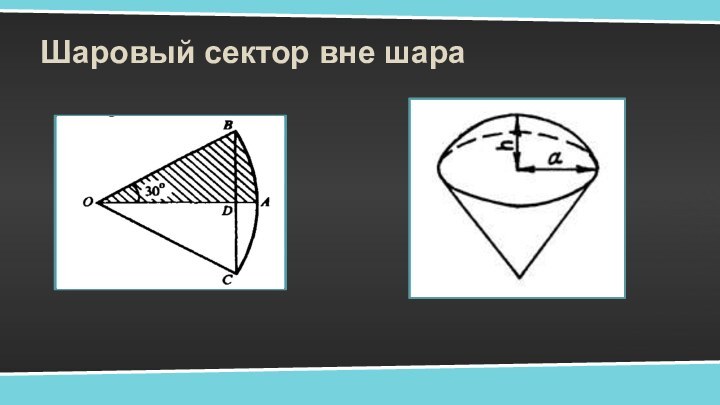
- 6. Шаровый сектор вне шара
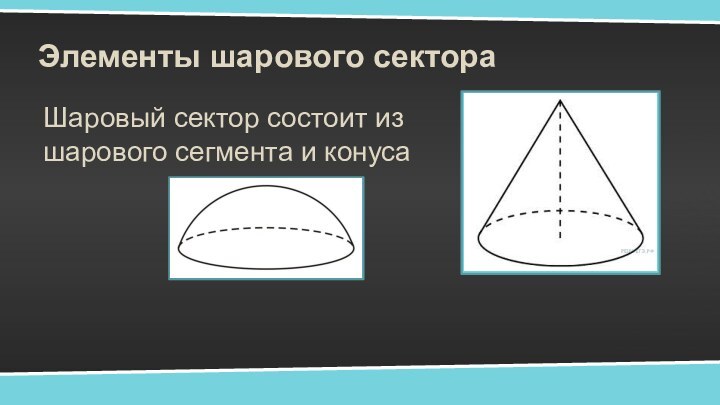
- 7. Элементы шарового сектораШаровый сектор состоит из шарового сегмента и конуса
- 8. Формулы шарового сектораОбъем шарового сектора вычисляется по формуле где r- радиус шара, h- высота сегмента
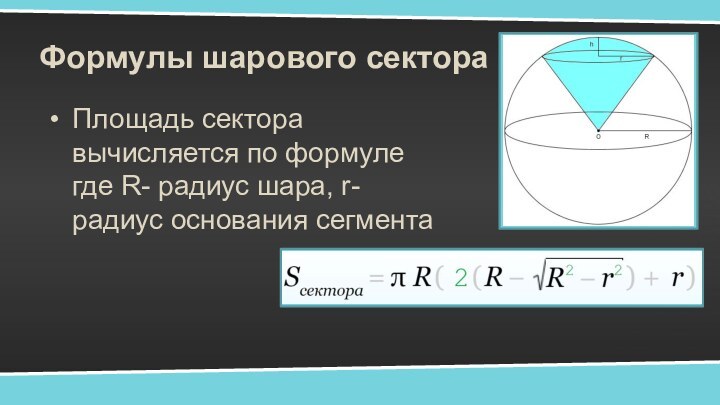
- 9. Формулы шарового сектораПлощадь сектора вычисляется по формуле где R- радиус шара, r- радиус основания сегмента
- 10. Шаровый слой-наз. часть шара заключенная между двумя параллельными секущими плоскостями
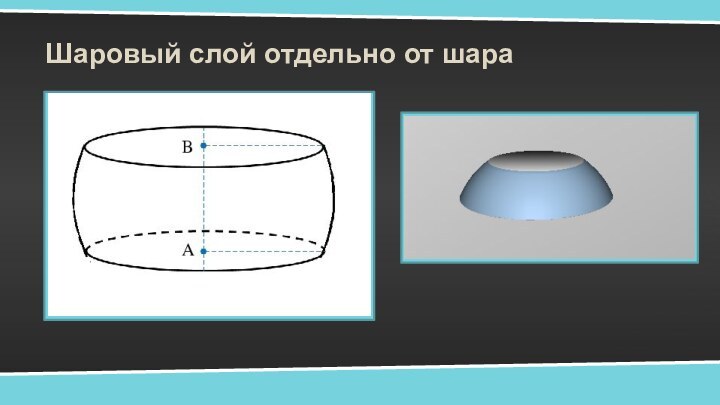
- 11. Шаровый слой отдельно от шара
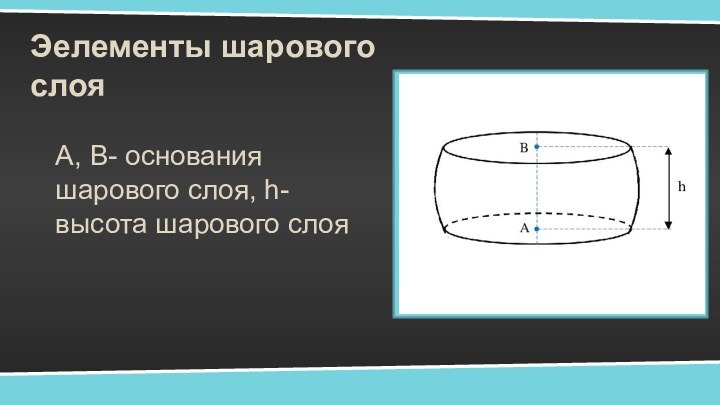
- 12. Эелементы шарового слояА, B- основания шарового слоя, h- высота шарового слоя
- 13. Формулы шаровго слояОбъем шарового слоя вычисляется из разности двух шаровых сегментовV1V2
- 14. Задача о параллелограмме наибольшей площади, который можно
- 15. Скачать презентацию
- 16. Похожие презентации
Шаровый сегмент вне шара
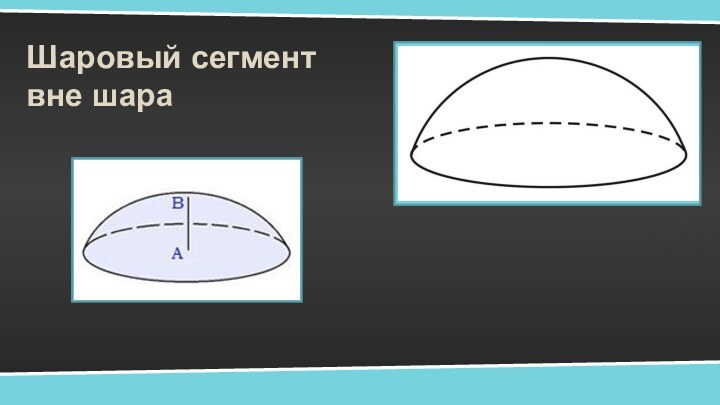








Слайд 4
Формулы шарового сегмента
объем шарового сегмента вычисляется по формуле,
где R-радиус шара, h- высота
площадь поверхности вычисляется по формуле
где R- радиус шара h- высота шарового сегмента
Слайд 5
Шаровый сектор
-наз. тело, полученное вращением кругового сектора с
углом, меньше 90 градусов, вокруг прямой , содержащии один
из ограничивающих круговой сектор радусов один из ограничивающих круговой сектор радиусов
Слайд 8
Формулы шарового сектора
Объем шарового сектора вычисляется по формуле
где r- радиус шара, h- высота сегмента
Слайд 9
Формулы шарового сектора
Площадь сектора вычисляется по формуле где
R- радиус шара, r- радиус основания сегмента
Слайд 14
Задача о параллелограмме наибольшей площади, который можно вписать
в треугольник приводится в “Началах” Евклида (III в. до
н. э.); задача о шаровом сегменте максимального объема при заданной площади шаровой части поверхности этого сегмента содержится в сочинениях Архимеда (тоже III в. до н. э.)Историческая справка