Презентация на тему Золотое сечение в математике и в жизни

Пифагора и деление отрезка в крайнем и среднем отношении.

Первое можно сравнить с ценность золота, второе можно назвать драгоценным камнем».
Иоганн Кеплер

происхождения, алгебраическое нахождение «золотого сечения», геометрическое построение «золотого сечения».
2.

Рассмотреть применение «золотого сечения» в архитектуре Древней Греции.
3. Рассмотреть «золотое сечение» как гармоническую пропорцию.
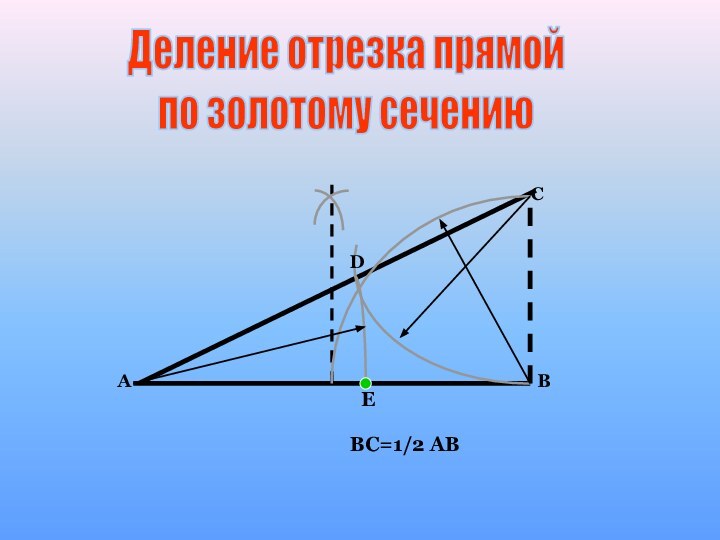
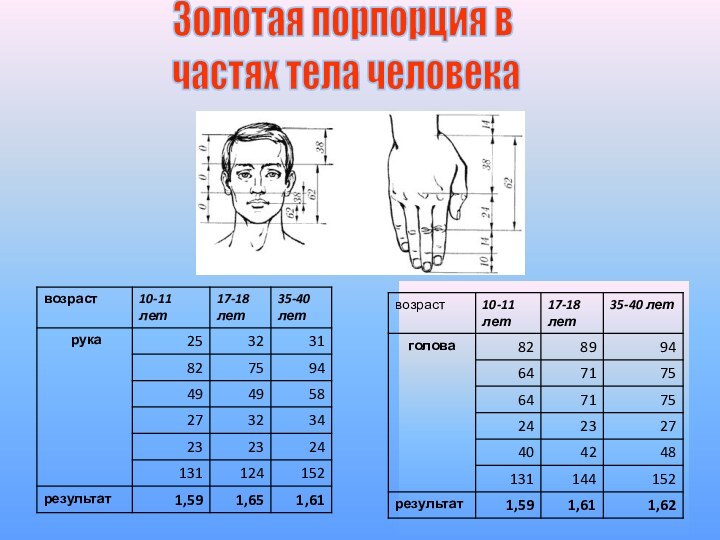
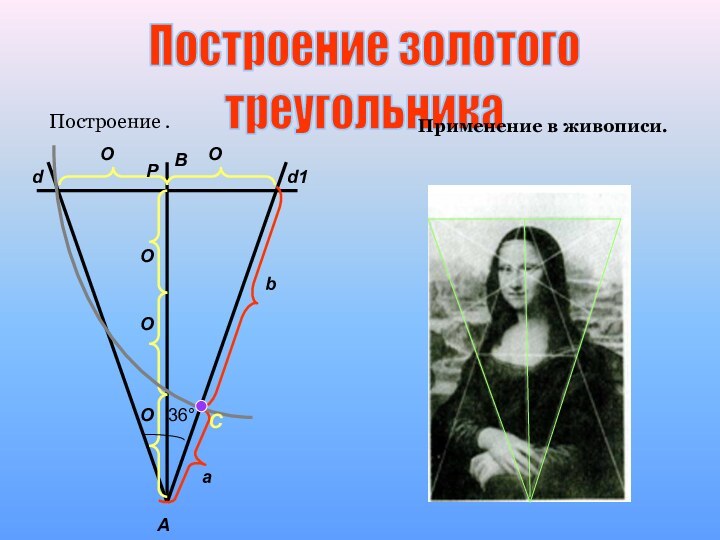
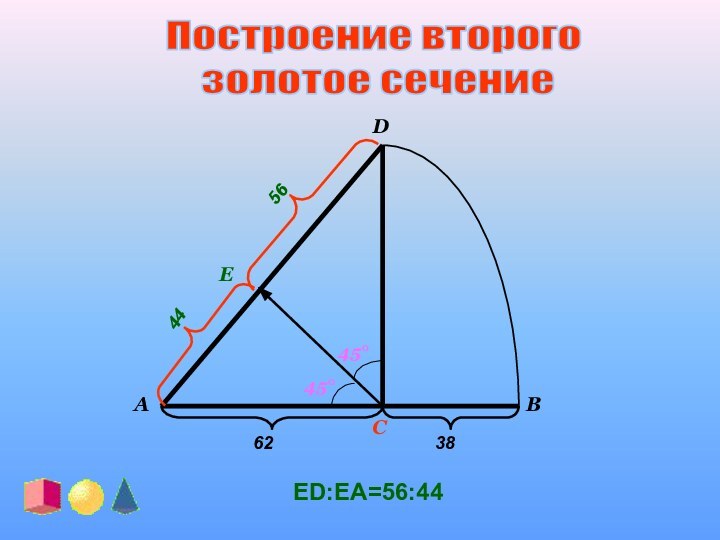
4. Изучить такие понятия как «второе золотое сечение», «золотой треугольник».
5. Постараться найти в окружающем меня мире применение этих понятий.

материалами для более подробного изучения темы «золотое сечение», дать

наиболее полное представление о данной теме; рассмотреть применение «золотого сечения» в архитектуре городов Тверской области.

деление отрезка на неравные части, при котором весь отрезок

так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

- Золотое сечение

Иоанна Богослова

человек интуитивно подстраивал струны так, чтобы они создавали благозвучие.

Пифагору принадлежит математическое объяснение основ гармонии; по его определению, наиболее естественно воспринимаются человеком частоты, которые находятся между собой в простых числовых отношениях. Вот откуда и отношение частот в октаве 1: 2, и благозвучное трезвучие с отношением частот 4: 5: 6. Уменьшая последовательно длины струн, мы получим природный звукоряд из 16 звуков, но почему же древние музыканты приняли звукоряд, состоящий из семи основных звуков, и лишь позже добавили еще пять дополнительных (так появились черные клавиши в пианино).Значение работ Пифагора по научному объяснению основ музыкальной гармонии трудно переоценить. Это была первая научно обоснованная теория гармонии в музыке. Познав истинность и красоту своей музыкальной теории, Пифагор пытался распространить ее на космологию; по его представлениям, и планеты Солнечной системы располагались в соответствии с музыкальной октавой. Эта гипотеза Пифагора не потеряла своей привлекательности и в более поздние времена.

Золотое сечение в музыке

чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим

спиралям, завивающимся навстречу друг другу. Причем числа "правых "и "левых " спиралей, всегда относятся друг к другу, как соседние числа Фибоначчи В формулах листорасположения (филлотаксис) многих растений встречаются числа Фибоначчи, расположенные строго закономерно - через одно, например, орешник -1/3, дуб, вишня - 2/5, облепиха-5/13

роща» с очевидностью просматриваются мотивы золотого сечения. Ярко

освещенная солнцем сосна (стоящая
на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещённыйсолнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины
по золотому сечению и дальше.

от земной поверхности описывается следующей формулой:

где h - высота

над поверхностью Земли, R - ее радиус. При опускании тела в глубь Земли характер зависимости g от h меняется:

Когда gh=g-h? Ясно, что одним из решений будет h=0. Второе решение таково:

Мы видим в решении уже знакомую нам формулу золотого сечения.