- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему мастер-класс Способы решения нестандартных математических задач как средство достижения планируемых результатов статья по математике (4 класс)
Содержание
- 2. Предметные знания и умения, приобретённые при изучении
- 3. Не мыслям надобно учить, а учить мыслить.Э. Кант.
- 4. задачи математического образованиясформировать набор необходимых для дальнейшего
- 5. Арифметический способ1-ый способЕсли за исходное рассмотреть отношение
- 6. Алгебраический способх- вёдер под 1 сливу;3х –
- 7. Графический способИз двух пунктов навстречу друг другу
- 8. Практический способВ гараже 20 легковых и грузовых
- 9. Схематический способЗадача. Собрался Иван-царевич на бой с
- 10. Табличный способБеседуют трое друзей: Белов, Рыжов и
- 11. Перебор вариантов (метод полной или частичной
- 12. Предположение ответа (метод ложного ответа)Отец обещал сыну
- 13. Скачать презентацию
- 14. Похожие презентации










Слайд 4
задачи математического образования
сформировать набор необходимых для дальнейшего обучения
предметных и общеучебных умений на основе решения как предметных,
так и интегрированных жизненных задач;обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования; обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;
сформировать устойчивый интерес к математике на основе дифференцированного подхода к учащимся;
выявить и развить математические и творческие способности на основе заданий, носящих нестандартный, занимательный характер.
Слайд 5
Арифметический способ
1-ый способ
Если за исходное рассмотреть отношение между
количеством деревьев (8 яблонь, 4сливы), то ответ на вопрос
задачи может быть получен путем выполнения следующих действий.1)8 : 4 = 2 (раз) — яблонь больше, чем слив;
2)2*3 = 6 (раз) — воды вылили больше под яблони;
3)1 + 6 = 7 (частей) — в общем объеме воды;
4)140 : 7 = 20 (вед.) — израсходовали на полив всех слив;
5)140 - 20 = 120 (вед.) — израсходовали на полив всех яблонь.
2-ой способ
Если рассуждать, начиная с отношения, зафиксированного в тексте задачи последним (на полив яблони уходит воды в 3 раза больше), то цепочка будет другой
1)8*3 = 24 (сл.) — можно полить вместо 8 яблонь;
2) 24 + 4 = 28 (сл.) — можно полить вместо 8 яблонь и 4слив
3)140 : 28 = 5 (вед.) — нужно для полива одной сливы;
4)5*4 =20 (вед.) — вылили под сливы;
5) 140 - 20 = 120 (вед.) — вылили под яблони.
Для полива 8 яблонь и 4 слив мальчики принесли 140 ведер воды. Сколько ведер воды вылили под яблони и сколько под сливы, если на полив одной яблони уходит воды в 3 раза больше, чем на полив одной сливы?
Всего 6 арифметических способов решения задачи
Слайд 6
Алгебраический способ
х- вёдер под 1 сливу;
3х – вёдер
под 1 яблоню;
4х- вёдер под 4 сливы;
3х*8=24х- вёдер под
8 яблонь.Всего: 4х+24х=140 вёдер
Решив уравнение, находим х=5, значит,
на полив слив израсходовали 20 вёдер, а на полив яблонь - 120 вёдер.
Слайд 7
Графический способ
Из двух пунктов навстречу друг другу выехали
два велосипедиста. Первый проехал 1/3пути, второй —5/8 пути. Произошла
ли встреча велосипедистов?Находим 1/3 пути (делим отрезок на 3 равные части и берём 1 часть)
Находим 5/8пути (делим на 8 частей и показываем 5 таких частей)
Как показывает чертёж, встреча не произошла.
1/3=8/24
5/8=15/24
Слайд 8
Практический способ
В гараже 20 легковых и грузовых автомобилей,
причем на каждую легковую машину приходится 4 грузовые. Сколько
легковых и сколько грузовых машин в гараже?Изобразим, что на 1 легковую машину приходится 4 грузовые:
Л-Г-Г-Г-Г-5 машин,
дальше нетрудно сообразить, что 20 машин разделить на 5, получится 4 раза:
Л-Г-Г-Г-Г-5 машин
Л-Г-Г-Г-Г-5 машин
Л-Г-Г-Г-Г-5 машин
Подсчитаем количество легковых машин (4) и грузовых: 4*4=16(грузовых)
Слайд 9
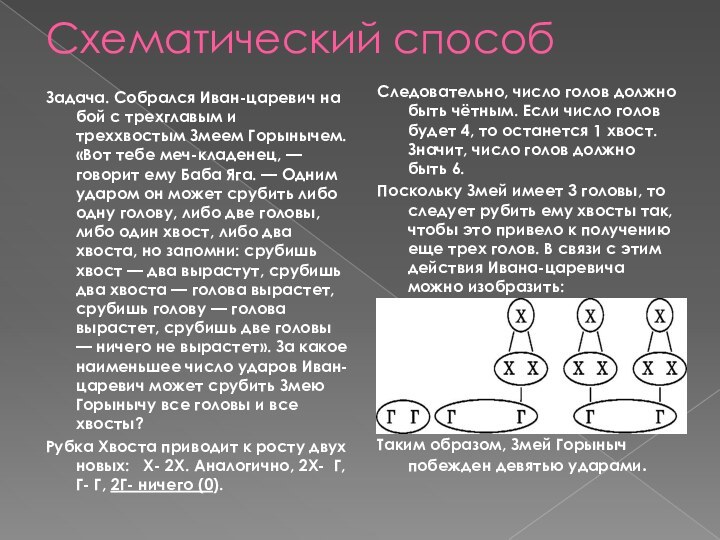
Схематический способ
Задача. Собрался Иван-царевич на бой с трехглавым
и треххвостым Змеем Горынычем. «Вот тебе меч-кладенец, — говорит
ему Баба Яга. — Одним ударом он может срубить либо одну голову, либо две головы, либо один хвост, либо два хвоста, но запомни: срубишь хвост — два вырастут, срубишь два хвоста — голова вырастет, срубишь голову — голова вырастет, срубишь две головы — ничего не вырастет». За какое наименьшее число ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?Рубка Хвоста приводит к росту двух новых: Х- 2Х. Аналогично, 2Х- Г, Г- Г, 2Г- ничего (0).
Следовательно, число голов должно быть чётным. Если число голов будет 4, то останется 1 хвост. Значит, число голов должно быть 6.
Поскольку Змей имеет 3 головы, то следует рубить ему хвосты так, чтобы это привело к получению еще трех голов. В связи с этим действия Ивана-царевича можно изобразить:
Таким образом, Змей Горыныч побежден девятью ударами.
Слайд 10
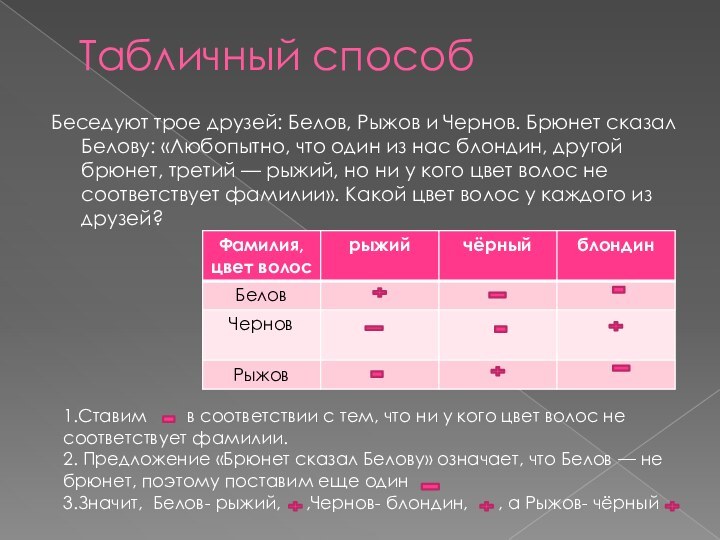
Табличный способ
Беседуют трое друзей: Белов, Рыжов и Чернов.
Брюнет сказал Белову: «Любопытно, что один из нас блондин,
другой брюнет, третий — рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?1.Ставим в соответствии с тем, что ни у кого цвет волос не соответствует фамилии.
2. Предложение «Брюнет сказал Белову» означает, что Белов — не брюнет, поэтому поставим еще один
3.Значит, Белов- рыжий, ,Чернов- блондин, , а Рыжов- чёрный
Слайд 11
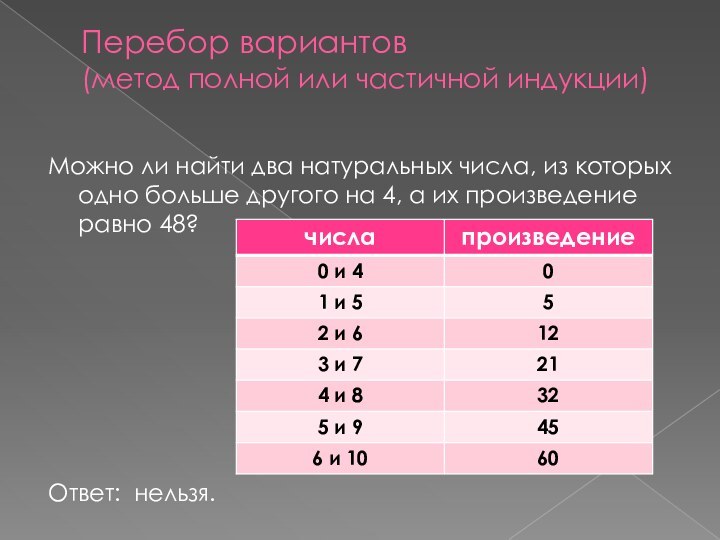
Перебор вариантов
(метод полной или частичной индукции)
Можно ли
найти два натуральных числа, из которых одно больше другого
на 4, а их произведение равно 48?Ответ: нельзя.
Слайд 12
Предположение ответа
(метод ложного ответа)
Отец обещал сыну за каждую
правильно решенную задачу опускать в копилку 10 монет, а
за каждую неправильно решенную задачу сын должен возвращать отцу по 5 монет. После того как было решено 20 задач, у сына в копилке оказалось 80 монет. Сколько задач сын решил неправильно и сколько без ошибок?Пусть 10 задач решено верно. В копилке окажется при этом:
10*10 -5*10=50(мон.).Получили, что 50 < 80 (отклонение отрицательно). При принятой гипотезе количество денег уменьшилось бы на 80 - 50=30(мон.). За каждую правильно решенную задачу вернем по 10+ 5 =15 (мон.).Теперь узнаем, на сколько принятая гипотеза меньше истинного ответа: 30 : 15 =2 (зад.), поэтому количество задач, решенных без ошибок, составит 10 + 2 =12 (зад.), а неправильно решенных 10 - 2 =8(зад.) или 20 - 12 =8(зад.). Способом установления соответствия между данными и искомыми легко определяется правильность решения предложенной задачи: 10*12 - 5*8 =80 (мон.).





























