Слайд 2
Освоение методики расчета индивидуальных режимов дозирования лекарственных препаратов
с помощью реализации на компьютере средствами Microsoft Excel простейших
математических моделей фармакокинетики
ЦЕЛЬ ЗАНЯТИЯ
Слайд 3
Актуальность и доступность для врача решения поставленных задач
с помощью компьютера
Актуальность: Необходимость индивидуали-зации режимов фармакотерапии с учетом фармакокинетики
препарата и особенностей каждого пациента с целью получения наилучшего терапевтического эффекта и исключения токсического действия препарата
Доступность: Решение фармакокинетических задач стандартными программными средствами современных компьютеров не требует специальной компьютерной или математической подготовки
Слайд 4
Базисные знания:
Для успешного освоения материала занятия студенты должны
владеть следующими базисными знаниями и навыками:
Математика: в объеме курса
средней школы
Фармакология (общий курс)
Общая физика (фундаментальные законы природы)
Начальные навыки работы с компьютером
Слайд 5
Компьютерное моделирование для решения задач фармакокинетики.
Математические камерные фармакокинетические
модели внутривенного и внутримышечного введения лекарственных препаратов.
Компьютерная реализация моделей
средствами Microsoft Excel /
Расчет индивидуального режима дозирования лекарственных препаратов с использованием математических моделей фармакокинетики.
Слайд 6
Определим математическую модель некоторой системы, как такое математическое
описание этой системы, которое может быть использовано вместо реальной
системы при решении некоторых практических или научных задач.
Фармакокинетика — раздел клинической фармакологии, предметом которого является изучение процессов всасывания, распределения, связывания с белками, биотрансформации и выведения лекарственных веществ.
Фармакокинетику условно можно разделить на теоретическую и прикладную. Теоретическая ФК изучает закономерности распределения ЛС в организме, а прикладная на основе этих закономерностей решает задачу выбора индивидуального режима введения препарата.
Слайд 7
5
100 mg/min
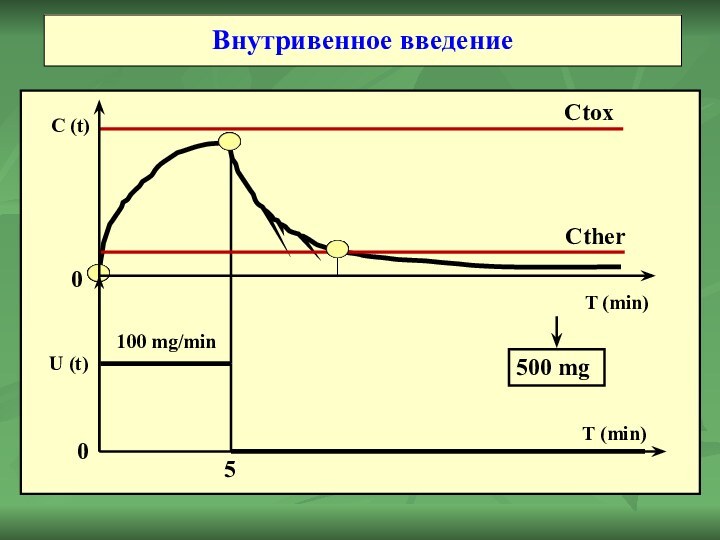
Внутривенное введение
Слайд 8
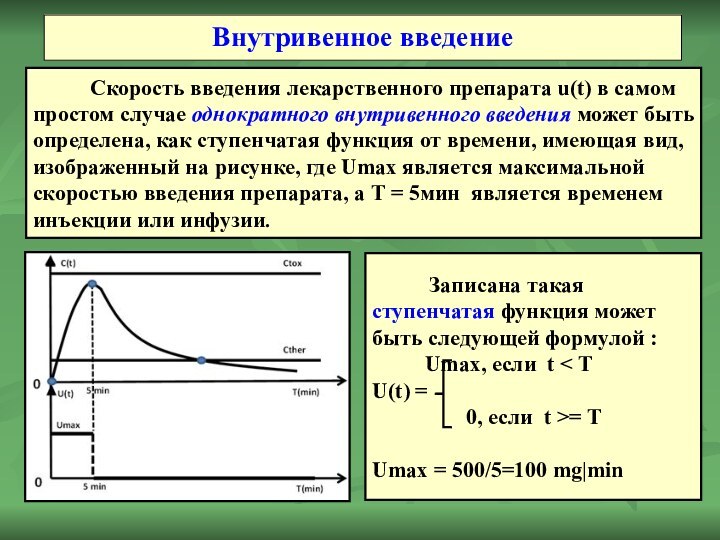
Скорость введения лекарственного препарата u(t) в самом простом
случае однократного внутривенного введения может быть определена, как ступенчатая
функция от времени, имеющая вид, изображенный на рисунке, где Umax является максимальной скоростью введения препарата, а T = 5мин является временем инъекции или инфузии.
Записана такая ступенчатая функция может быть следующей формулой :
Umax, если t < T
U(t) =
0, если t >= T
Umax = 500/5=100 mg|min
Внутривенное введение
создания математических фармакокинети-ческих моделей является понятие «камера».
Начало развития фармакокинетики как самостоятель-ного раздела общей фармакологии связывают с возникно-вением учения о гистогематических барьерах, предложен-ного Л.С. Штерн в 1918 г.
Благодаря этому учению сложилось представление о существовании в организме жидкостей, относительно изолированных друг от друга.
Попадая в какую-либо из них, лекарственное вещество (ЛВ) имеет ограниченную возможность проникновения в другую.
Камера (compartment) представляет собой ограниченный не изменяющийся во времени объем жидкости (ткани), в котором ЛВ распределено равномерно.
Слайд 10
Математические модели, описывающие поведение препарата
в одном или нескольких объемах или камерах называются камерными
(компартментными) моделями.
Наиболее часто в фармакокинетике используется так называемая однокамерная модель распределения лекарства.
Эта модель предполагает, что вся доза препарата, введенного в организм человека, распределяется в одном объеме, который называется «кажущимся» объемом распределения препарата в организме и обозначается как Vd (apparent volume of distribution).
Слайд 11
Volume of distribution From Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Volume_of_distribution
Кажущийся объем распределения определяется, как некоторый гипотетический (идеальный)
объем, в котором распределилось бы общее количество введенного в организм препарата, если бы его концентрация C(t) в любой момент времени t равнялась концентрации в плазме крови.
Слайд 12
Схема ОДНОКАМЕРНОЙ фармакокинетической модели внутривенного введения препарата
На
схеме объем распределения рассматривается как камера, куда препарат поступает
со скоростью U(t) (зависит от заданного лечащим врачом режима дозирования), и откуда препарат выводится со скоростью элиминации Cl*C(t).
Выход препарата из организма хорошо описывается диффузией, т.е. скорость выхода пропорциональна концентрации препарата в объеме и может быть записана как Cl * C(t), где коэффициент Cl
(общий клиренс) еще одна фармакокинетическая константа.
Слайд 13
Определения основных фармакокинетических параметров, приводимых в справочнике лекарственных
препаратов
Кажущийся объем распределения Vd определяется, как некоторый идеальный объем,
в котором следовало бы распределить массу находящегося в организме пациента лекарственного препарата, чтобы его концентрация оказалась такой же, какая наблюдается в плазме крови.
Общий клиренс лекарственного вещества Cl определяется как объем плазмы крови, очищаемой от лекарственного вещества в единицу времени за счет действия всех выделительных систем организма.
Слайд 14
Определения основных фармакокинетических параметров, приводимых в справочнике лекарственных
препаратов
Концентрация терапевтическая Cther определяется как минимальная концентрация препарата
в крови, ниже которой препарат теряет лечебное действие
Концентрация токсическая Ctox определяется как минимальная концентрация препарата в крови, выше которой препарат начинает оказывать токсическое действие.
Слайд 15
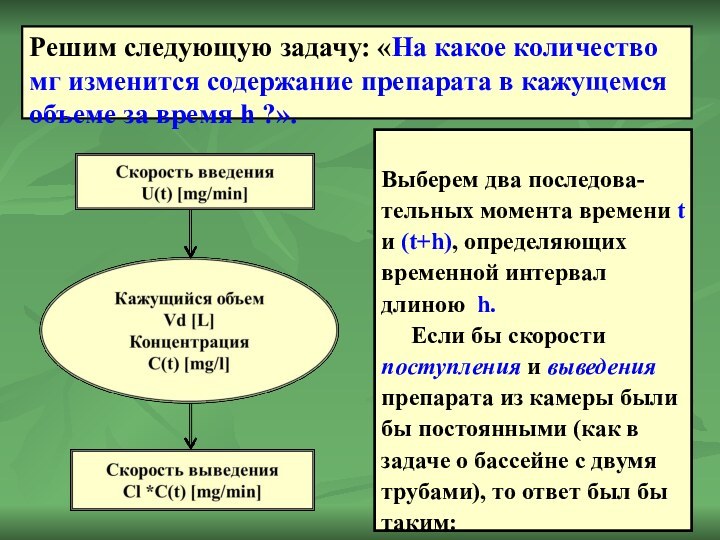
Выберем два последова-тельных момента времени
t и (t+h), определяющих временной интервал длиною h.
Если бы скорости поступления и выведения препарата из камеры были бы постоянными (как в задаче о бассейне с двумя трубами), то ответ был бы таким:
h*U(t) – h* Cl*C(t)
Решим следующую задачу: «На какое количество мг изменится содержание препарата в кажущемся объеме за время h ?».
Слайд 16
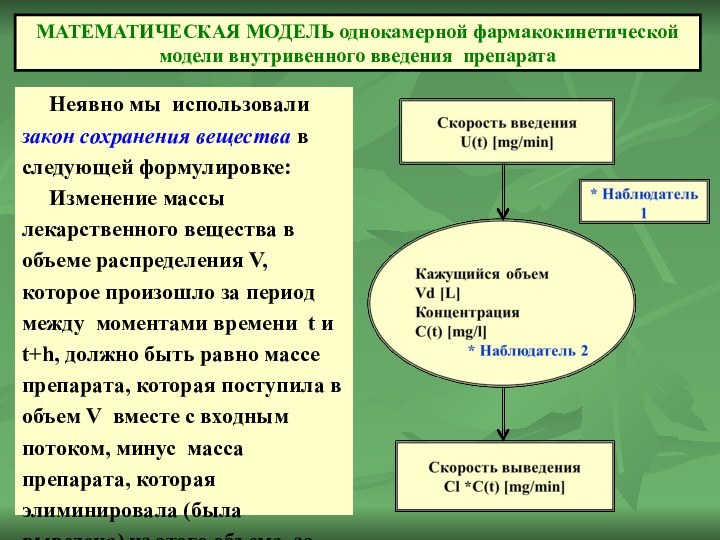
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ однокамерной фармакокинетической модели внутривенного введения препарата
Неявно мы использовали закон сохранения вещества в
следующей формулировке:
Изменение массы лекарственного вещества в объеме распределения V, которое произошло за период между моментами времени t и t+h, должно быть равно массе препарата, которая поступила в объем V вместе с входным потоком, минус масса препарата, которая элиминировала (была выведена) из этого объема за тот же период времени.
Слайд 17
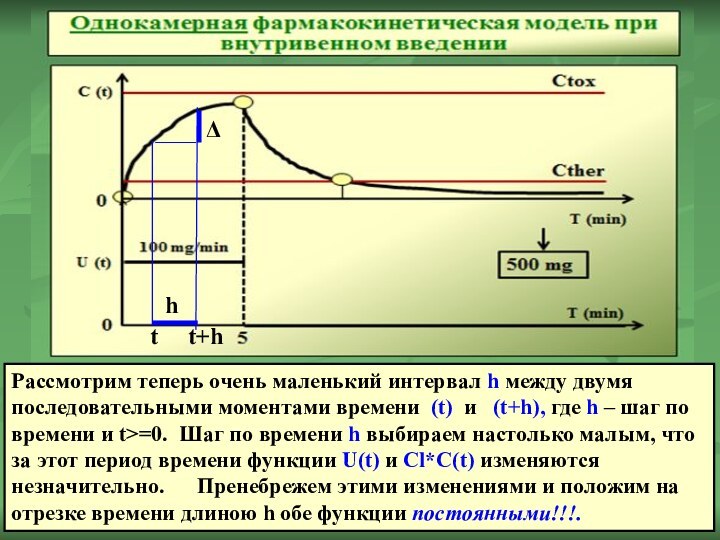
Рассмотрим теперь очень маленький интервал h между двумя
последовательными моментами времени (t) и (t+h), где h
– шаг по времени и t>=0. Шаг по времени h выбираем настолько малым, что за этот период времени функции U(t) и Cl*C(t) изменяются незначительно. Пренебрежем этими изменениями и положим на отрезке времени длиною h обе функции постоянными!!!.
Δ
Слайд 18
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ однокамерной фармакокинетической модели внутривенного введения препарата
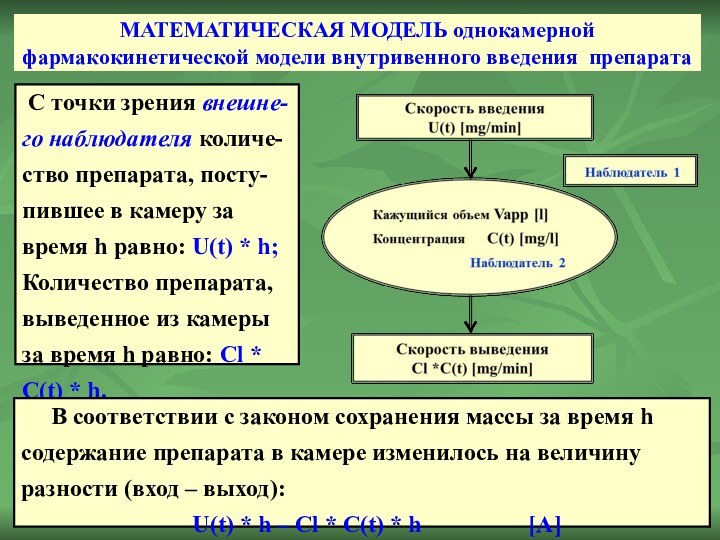
С точки зрения внешне-го наблюдателя количе-ство препарата, посту-пившее в
камеру за время h равно: U(t) * h;
Количество препарата, выведенное из камеры за время h равно: Cl * C(t) * h.
В соответствии с законом сохранения массы за время h содержание препарата в камере изменилось на величину разности (вход – выход):
U(t) * h ‒ Cl * C(t) * h [A]
Слайд 19
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ однокамерной фармакокинетической модели в/в введения препарата
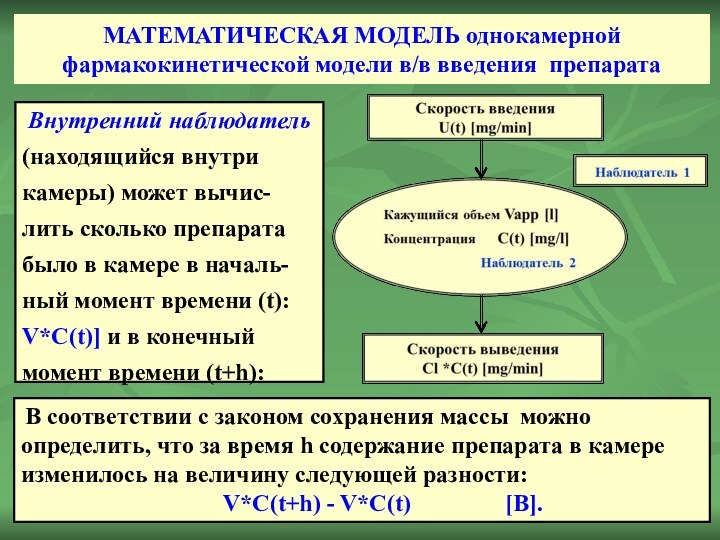
Внутренний наблюдатель (находящийся внутри камеры) может вычис-лить сколько препарата
было в камере в началь-ный момент времени (t): V*C(t)] и в конечный момент времени (t+h): V*C(t+h).
В соответствии с законом сохранения массы можно определить, что за время h содержание препарата в камере изменилось на величину следующей разности:
V*C(t+h) - V*C(t) [B].
Слайд 20
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ однокамерной фармакокинетической модели внутривенного введения
Закон сохранения
вещества позволяет приравнять результаты [A] и [B], полученные разными
наблюдателями, и мы получаем следующее математическое уравнение, описывающее однокамерную фармакокинетическую модель внутривенного введения препарата:
V*C(t+h) – V*C(t) = U(t)*h – Cl*C(t)*h (1)
Напомним, что мы пренебрегли малыми изменениями функций U(t) и Cl*C(t) за период времени h, начиная с момента времени t. Таким образом, уравнение (1) отражает закон сохранения массы только приближенно, однако, степень приближения всегда может быть выбрана приемлемой для практического использования за счет снижения величины шага по времени.
Слайд 21
ВЫЧИСЛЕНИЕ однокамерной фармакокинетической модели внутривенного введения препарата
Из уравнения
(1) величина C(t+h) может быть выражена следующим образом:
C(t+h) =
C(t) + h/V * [U(t) – Cl*C(t)] (2)
Как следует из уравнения (2), концентрация лекарственного вещества в момент времени (t+h) может быть вычислена, если известна концентрация этого вещества в предыдущий момент времени t.
Следовательно, начиная с этой начальной точки дальнейшая динамика концентрации может быть вычислена пошагово.
Напомним, что если препарат вводится впервые, то в момент времени 0 его концентрация в организме равна 0.
Таким образом, одна точка на графике нам известна всегда и мы можем вычислить всю кривую заранее, не проводя пробной инъекции с последующими контрольными измерениями для оценки правильности выбранной дозы.
Слайд 22
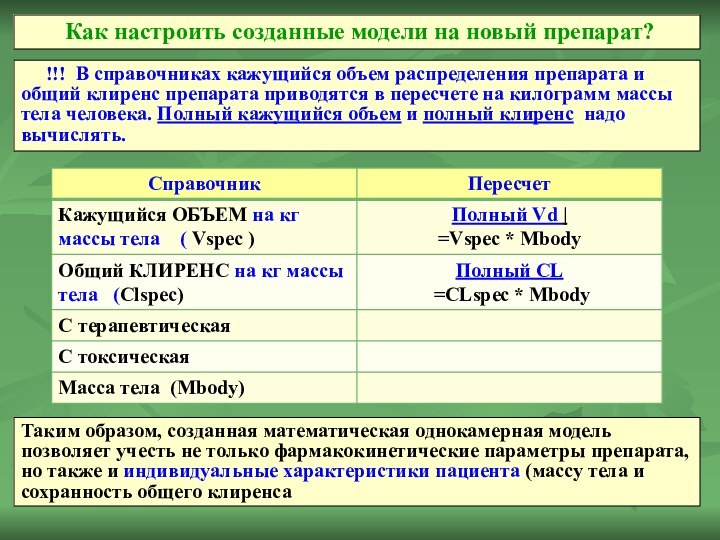
!!! В справочниках кажущийся объем
распределения препарата и общий клиренс препарата приводятся в пересчете
на килограмм массы тела человека. Полный кажущийся объем и полный клиренс надо вычислять.
Как настроить созданные модели на новый препарат?
Таким образом, созданная математическая однокамерная модель позволяет учесть не только фармакокинетические параметры препарата, но также и индивидуальные характеристики пациента (массу тела и сохранность общего клиренса
Слайд 23
Как учесть состояние общего клиренса у пациента?
Пусть
известно, что общий клиренс у пациента снижен на 30%,
то есть составляет 70% от полной сохранности
Для того, чтобы учесть это в нашей модели, в уравнение (2) должна быть внесена следующая поправка:
C(t+h) = C(t) + h/V * [U(t) – 0,7*Cl*C(t)] (2)
Таким образом, созданная математическая однокамер-ная модель позволяет учесть не только фармакокинети-ческие параметры препарата, но также и индивидуаль-ные характеристики пациента (массу тела и сохранность общего клиренса.
Слайд 24
В последние годы в литературе все чаще стали
звучать доводы в пользу индивидуализации дозирования на основе данных
клинической фармакокинетики, а терапевтические рамки предлагалось рассматривать только как общие рекомендации при поиске оптимального режима дозирования для каждого конкретного пациента.
Индивидуализация дозирования необходима в следующих ситуациях:
Когда существует значительная межиндивидуальная вариация фармакокинетических параметров препарата, что важно для детей, у которых имеются существенные различия в весе и скорости метаболизма.
Когда препарат имеет узкий терапевтический коридор - зона положительного эффекта находится достаточно близко от зоны побочных эффектов.
Когда у пациента есть болезни желудочно-кишечного тракта, печени или почек, влияющие на фармакокинетику, особенно на процессы абсорбции, метаболизма или экскреции.
Слайд 25
Индивидуализация дозирования на основе мониторинга
необходима в следующих ситуациях:
Когда выбор терапии
осуществляется для лечения специальных групп пациентов (беременных женщин, пожилых людей, новорожденных, детей и т.д.), так как у них фармакокинетические параметры и соответственно значения границ терапевтического коридора отличаются от обычных принятых средних значений.
Когда пациент получает политерапию, поскольку сочетания некоторых препаратов приводят к их взаимовлиянию, выражающемуся в изменении фармакокинетических параметров и в других ситуациях.
Для реализации подхода индивидуализации дозирования важное значение имеет появление все более совершенных компьютерных программ.
заместитель директора НИИ физико-химической медицины МЗ РФ член-корреспондент РАМН В.И. СЕРГИЕНКО
Слайд 26
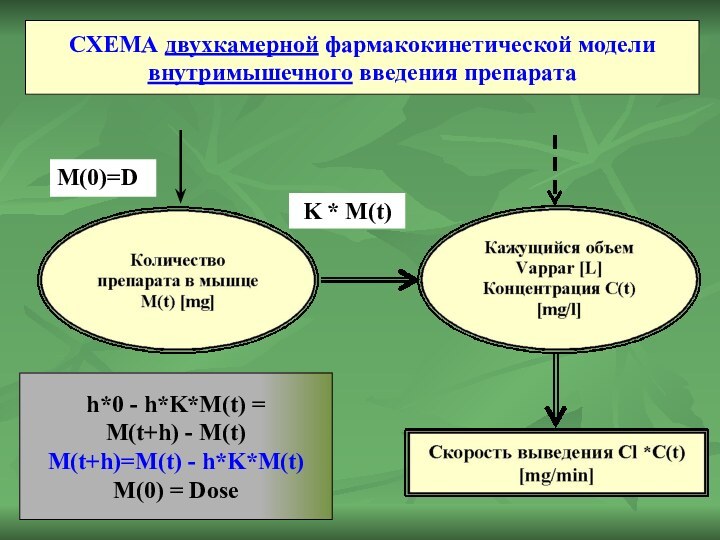
СХЕМА двухкамерной фармакокинетической модели внутримышечного введения препарата
M(0)=D
K *
M(t)
h*0 - h*K*M(t) =
M(t+h) - M(t)
M(t+h)=M(t) - h*K*M(t)
M(0) =
Dose
Слайд 27
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ двухкамерной фармакокинетической модели внутримышечного введения препарата
Применяя
закон сохранения массы к количеству лекарственного вещества, содержащегося в
мышце, и к количеству лекарственного вещества в кажущемся объеме получим 2 уравнения:
C(t+h) = C(t) +[λ*M(t) – CL*C(t)]*h/V (3)
M(t+h) = M(t) - λ*M(t)*h (4)
Начальные условия при t=0 :
M(0) = D, C(0) = 0 (5)
где λ – коэффициент скорости диффузии препарата из мышцы в кровь, D – доза препарата.
Слайд 28
Практические занятия включают выполнение следующих заданий:
Создание компьютерной реализации
двух фармакокинетических моделей - одно- и двухкамерной моделей внутривенного
и внутримышечного введения лекарственного препарата.
Настройка моделей на конкретный препарат и подбор фармакокинетических параметров препарата по результатам испытаний.
Подбор индивидуального режима внутривенного и внутримышечного введения препарата.
Модификация двух созданных компьютерных фармакокинетических моделей для воспроизведения режима длительного (периодического) в/в и в/м введения лекарственного препарата
Создание вариантов модели непрерывного внутривенного введения препарата (инфузия) .
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ.
Слайд 29
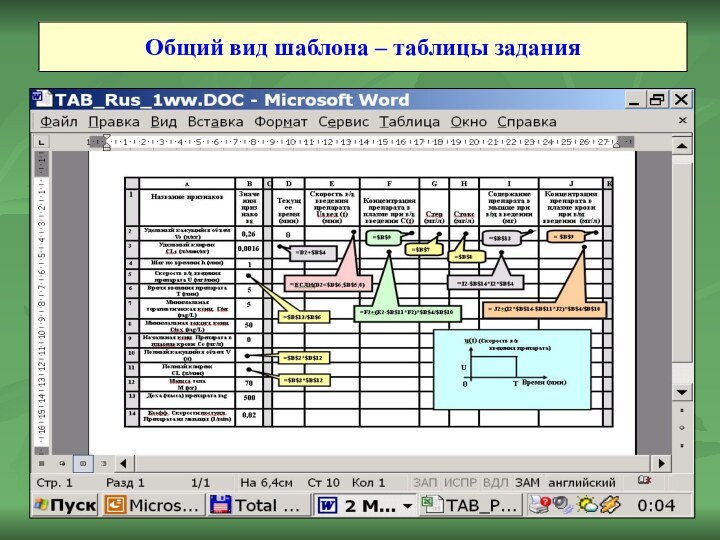
Общий вид шаблона – таблицы задания
Слайд 30
1-е задание заключается в выполнении компьютерной реализации двух
математических моделей, описывающих фармакокинетику препарата при в/в введении (однокамерная
модель) и при в/м введении (двухкамерная модель), уравнения для которых, были выведены на лекции.
На следующих слайдах последовательно описаны основные шаги решения 1-й задачи средствами программы Microsoft Excel.
Задание 1
Слайд 31
На рабочем столе расположена иконка шаблона-задания. Двойным щелчком
мыши шаблон-задание раскрывается.
На экране появляется фрагмент электронной таблицы
Microsoft Excel с двумя размеченными таблицами.
1-я таблица (столбцы A – B) предназначена для занесения значений параметров модели. Названия параметров заранее занесены в шаблон.
2-я таблица (столбцы D – J) предназначена для проведения вычислений значений переменных величин, входящих в модели. Названия переменных величин также заранее занесены в шаблон.
ШАБЛОН задания.
!!! ШАБЛОН сразу же необходимо запомнить под своим именем на диске С в папке (например, Pediatr 2015).
Слайд 32
Общий вид шаблона (программа Microsoft Excel) для компьютерной
реализации фармакокинетических моделей: однокамерной (в/в введение препарата) и двухкамерной
(в/м введение)
Слайд 33
Перед началом работы с электронной таблицей
сообщаем минимально необходимые сведения о правилах записи текстов и
формул в пакете Microsoft Excel :
В любую ячейку таблицы может быть записан текст или формула.
Все выполняемые математические действия производятся с содержимым ячеек, поэтому формулы записываются в терминах адресов ячеек.
Любая формула в Microsoft Excel начинается со знака «°=°». Как только знак равенства записан в ячейку, в электронной таблице появляется новая возможность - для записи адреса ячейки достаточно «кликнуть» на эту ячейку левой кнопкой мыши и ее адрес вставится в формулу.
Завершается любая запись в ячейке нажатием клавиши ENTER. Если формула записана правильно, то в ячейке с формулой окажется результат вычисления (число), а саму формулу можно прочитать в строке редактирования в верхней части экрана, если выделить эту ячейку.
Слайд 34
1) Заполняем столбец значений параметров модели
(столбец «В») всеми заданными в таблице-задании значениями параметров.
2)
Заполняем пропущенные ячейки в столбце значений параметров вычисляемыми значениями параметров.
В столбце «В» вычисляются следующие параметры:
Максимальная скорость в/в введения препарата
(в ячейке В6) по формуле
= доза / время введения (=В13/В6);
Полный кажущийся объем препарата (в ячейке В10) по формуле
= удельный кажущийся объем * массу тела (=В2*В12);
Полный клиренс препарата (в ячейке В11) по формуле:
= удельный клиренс * массу тела (=В3*В12).
Задание 1. Этапы 1-2
Слайд 35
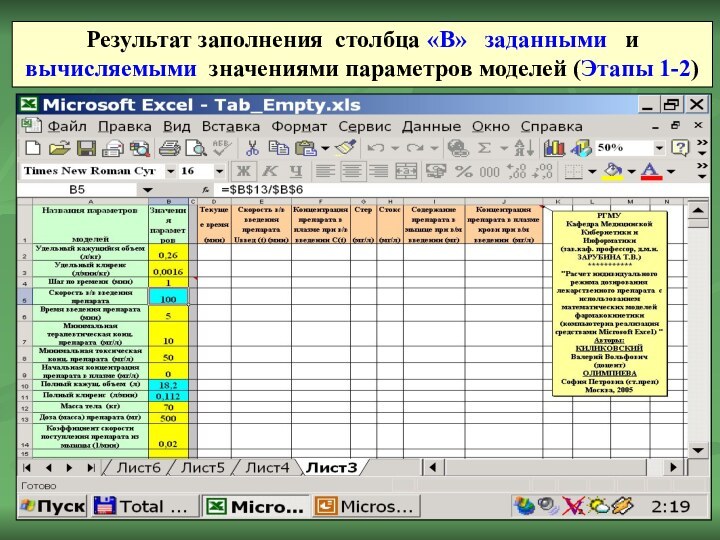
Результат заполнения столбца «В» заданными и
вычисляемыми значениями параметров моделей (Этапы 1-2)
Слайд 36
Переходим к вычислению формул во 2-й таблице.
Этап 3.

В столбце «D» проводим вычисление значений последовательных моментов времени
с заданным в ячейке «В4» шагом.
Для этого:
в ячейку «D2» записываем начальный момент времени, равный 0;
в ячейку «D3» записываем уравнение для вычисления следующего момента времени = D2+$B$4; после нажатия ENTER в ячейке «D3» появляется 1 (результат вычисления).
Для вычисления последующих значений времени формулу, записанную в ячейке «D3» «растягиваем» вниз по столбцу «D» на несколько следующих ячеек. Для этого выделив ячейку «D3» двигаем курсором мыши по ячейке до тех пор, пока в нижнем правом углу ячейки не появится черный крестик «+». Фиксируем его, нажав левую клавишу мыши, и перемещаем (тянем) курсор вниз по столбцу «D» на 10-12 ячеек. При таком движении в каждую следующую ячейку переписывается исходная формула, при этом адрес переменной ячейки увеличивается на 1, а адрес параметра, отмеченный символами «$», не меняется.
!!! Символы «$», записанные перед каждой буквой в адресе ячейки В4, содержащей параметр «шаг по времени», означают, что это постоянная величина (параметр) и в процессе растяжения формулы адрес этой ячейки не изменяется. Для того, чтобы перед буквенной и цифровой частью адреса ячейки появился символ «$», необходимо после записи адреса нажать функциональную клавишу “F4” в верхнем ряду клавиатуры.
Слайд 37
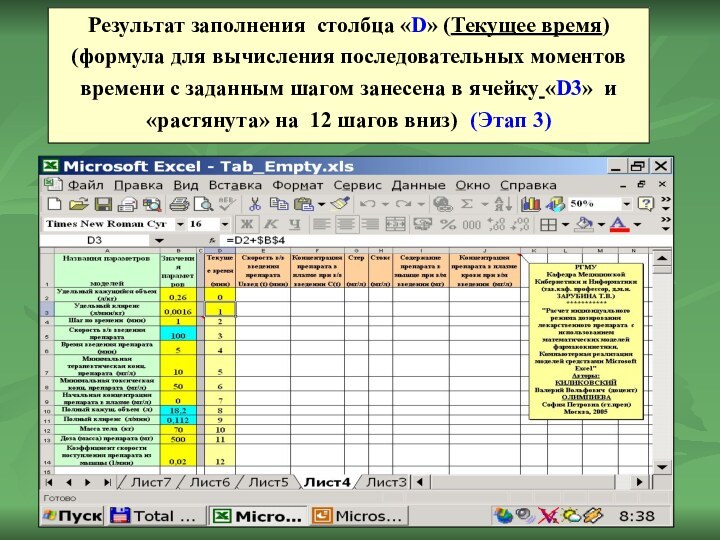
Результат заполнения столбца «D» (Текущее время) (формула для
вычисления последовательных моментов времени с заданным шагом занесена в
ячейку «D3» и «растянута» на 12 шагов вниз) (Этап 3)
Слайд 38
Этап 4. Для вычисление значений скорости в/в введения
в последовательные моменты времени в ячейку «E2» записываем условный
оператор ЕСЛИ, который имеет следующий вид:
=ЕСЛИ(D2<$В$6;$B$5;0).
Для вычисления условного оператора ЕСЛИ можно использовать шаблон, предоставляемый Microsoft Excel. В этом шаблоне предусмотрены три заполняемых окна, в которые вводятся:
1)°условие, которое проверяется (D2<$B$6);
2)°значение, которое принимает скорость введения, если условие выполнено (истинно) – ($B$5);
3)°значение, которое принимает скорость введения, если условие не выполнено (ложно). – в нашем случае это число 0.
ШАБЛОН открывается при внесении в ячейку знака “=“
Слайд 39
Этап 4. На четвертом этапе проводим вычисление

значений скорости внутривенного введения препарата в последовательные моменты времени.
!!!
Напоминаем, что все ячейки столбца В, использованные
в формуле, должны быть зафиксированы (символ $ перед буквенной и числовой частью адреса).
После нажатия клавиши ENTER в ячейке «E2» появляется число 100 (результат вычисления скорости в момент времени 0).
Для вычисления значений скорости в/в введения в последующие моменты времени формулу, записанную в ячейке «E2», «растягиваем» вниз по столбцу «E» на несколько следующих ячеек. Для этого двигаемся курсором мыши по ячейке «E2» до тех пор, пока в нижнем правом углу ячейки не появится черный крестик «+». Фиксируем его, нажав левую кнопку мыши, и, не отпуская кнопку, перемещаем (тянем) курсор вниз по столбцу «E» на 10-12 ячеек, но не дольше, чем «растянута формула в столбце «D».
!!! Если соседний столбец уже заполнен на несколько строк (в нашем случае это столбец D), то вместо растяжения формулы можно использовать двойной «клик» на черном крестике.
Слайд 40
Заполнение столбца «Е» (Скорость в/в введения). В ячейку
«Е3» формула вычисления скорости в/в введения в момент Т=0
записывается с использованием шаблона для логической функции «ЕСЛИ») (Этап 4)
Слайд 41
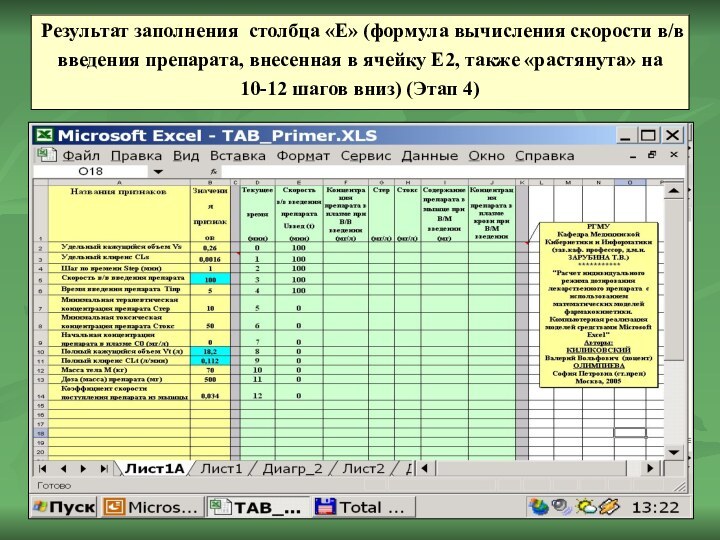
Результат заполнения столбца «Е» (формула вычисления скорости в/в
введения препарата, внесенная в ячейку Е2, также «растянута» на
10-12 шагов вниз) (Этап 4)
Слайд 42
На пятом – восьмом шагах проводим вычисление значений
следующих функций:
- концентрация лекарственного вещества при его внутривенном
введении (столбец F);
- терапевтическая и токсическая концентрации препарата (столбцы G, H);
- количество лекарственного вещества в мышце при внутримышечном введении (столбец I);
- концентрация лекарственного вещества в плазме крови при его внутримышечном введении (столбец J);
После вычисления формулы в одной ячейке для вычисления значений каждой функции в последующие моменты времени формулу необходимо «растянуть» вниз на 10-12 шагов для того, чтобы убедиться в том, что поведение функции соответствует нашим представлениям.
!!! В каждом столбце растягиваем формулу из последней заполненной в этом столбце ячейки (1-ю или 2-ю).
Задание 1. Этапы 5-8
Слайд 43
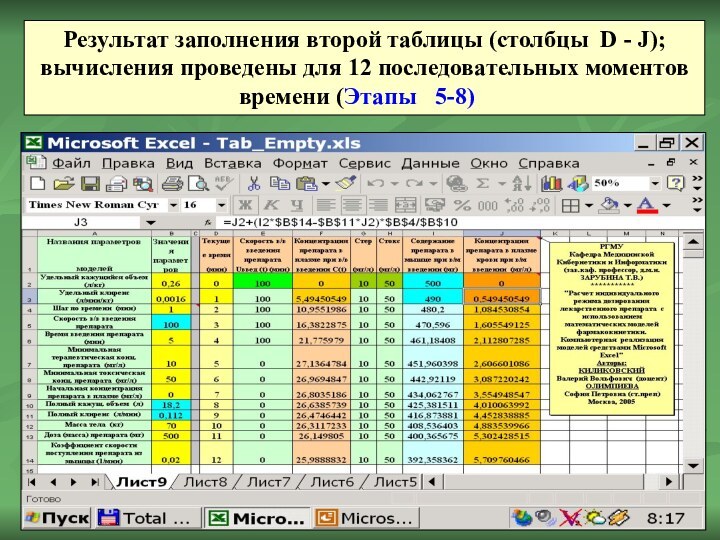
Результат заполнения второй таблицы (столбцы D - J);
вычисления проведены для 12 последовательных моментов времени (Этапы
5-8)
Слайд 44
!!! Вычисление всех функций во второй таблице с
помощью «растягивания» формул на 10-12 шагов необходимо для содержательного
контроля полученных результатов вычисления.
Например, необходимо убедиться, что при вычислении времени (столбец D) получились последовательные числа 0, 1, 2, 3 и т.д.; для концентрации в плазме препарата, введенного в/в (столбец F), имеет место увеличение значений, пока препарат вводится, то есть до 5-й минуты, и снижение значений, начиная с 5-й минуты) и т.д..
!!! Несоответствие этих результатов предполагаемому характеру изменения каждой из функций заставляет нас вернуться к формуле и проверить правильно ли она записана или составлена.
Этап 9. Примечание.
Слайд 45
Этап 9. Примечание. Что контролируется:
в столбце D

вычисляются моменты времени, для которых вычисляются все функции, поэтому
при шаге 1 минута в этом столбце должна появиться последовательность целых чисел. Если это не так, то, скорее всего, в функции, введенной в ячейку D3, забыли зафиксировать второе слагаемое ($B$4), задающее величину шага из первой таблицы;
в столбце E, вычисляется скорость введения препарата, которая в случае однокамерной модели, когда препарат вводится в течение 5 минут, равна 100 мг/мин, а далее, начиная с 5-й минуты (когда введение препарата заканчивается), эта скорость равна 0;
В столбце F, в котором вычисляется концентрация препарата в крови, контрольной точкой является достижение максимального значения на 5-й минуте (в момент прекращения введения препарата), а затем концентрация препарата медленно снижается;
В столбцах G и H вычисляются терапевтическая и токсическая концентрации, которые заданы для препарата и постоянны для всех моментов времени;
В столбце I вычисляется содержание препарата в мышце, которое должно медленно снижаться с уровня 500 мг (введенная доза);
В столбце J вычисляется концентрация препарата в крови при внутримышечном введении; для этой функции характерной динамикой является медленное увеличение концентрации.
Слайд 46
Для того, чтобы иметь возможность длительно следить
за изменениями концентрации препарата в плазме крови проведем вычисление
всех функций до 1000 – 1100 шагов.
Для этого в столбцах с D по J выделим ОДНУ!!! строку (например, соответствующую 10-му шагу, то есть выделим одновременно ячейки D12, Е12, F12, G12, H12, I12 и J12), в которых все функции вычислены, и «протянем» выделенный фрагмент таблицы за черный крестик в правом нижнем углу до 1000-го шага.
При величине шага 1 минута это соответствует длительности наблюдения за уровнем концентрации введенного препарата около 17 часов.
Задание 1. Этап 9
Слайд 47
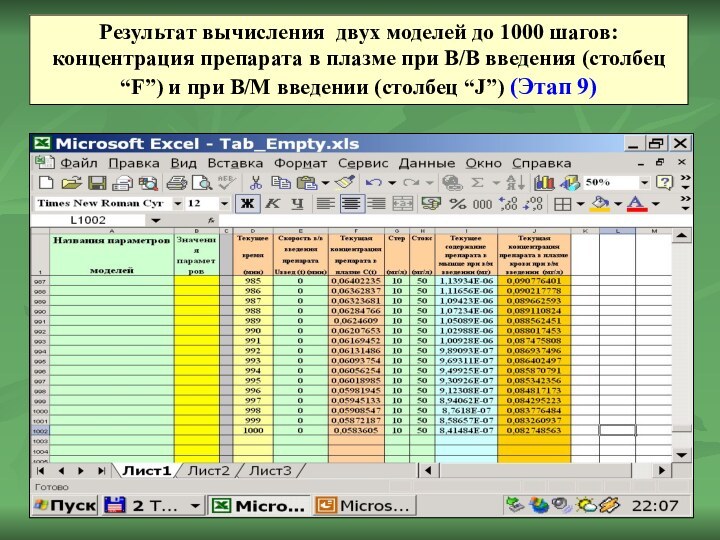
Результат вычисления двух моделей до 1000 шагов: концентрация
препарата в плазме при В/В введения (столбец “F”) и
при В/М введении (столбец “J”) (Этап 9)
Слайд 48
Построение графиков вычисленных функций.
Для организации визуального контроля
за измене-ниями концентрации препарата в плазме крови при разных
режимах его введения построим на отдельном листе графики всех функций, которые мы вычисляли.
Выделим все столбцы 2-й таблицы с вычисленными числовыми рядами и их названиями. Для этого, наведя курсор на название первого из вычисленных столбцов – D (на сером фоне), зафиксируем левую клавишу мыши и, не отпуская ее, протянем вправо по названиям остальных столбцов ( Е, F, G, H, I и J).
Найдем в верхней части экрана иконку, изображаю-щую гистограмму, и кликнем на нее мышкой. На экране появится самостоятельный модуль программы EXCEL под названием «Мастер диаграмм», который будет по шагам управлять нашими действиями при создании графиков.
!!! Из всех вариантов гистограмм выбираем «точечную», как единственную, в которой значения первого выделен-ного столбца используются в качестве шкалы по оси «Х».
Слайд 49
Построение графиков вычисленных функций.
На последнем шаге работы

с «Мастером диаграмм» выбираем вариант «на отдельном» листе. На
экране появятся графики всех выделенных нами функций. Однако, интересующие нас более всего графики изменения концентрации препарата в плазме оказались очень мелкими. Это связано с тем, что общий график масштабируется по самому высокому графику.
Удалим «лишние» графики. Первым удалим график, отображающий изменение содержания препарата в мышце при в/м введении. Удалим этот график с общего рисунка, для чего наведем на любую точку графика курсор (появится заголовок графика) и кликнем правой кнопкой мыши. Появится меню, в последней строке которого стоит вариант «удалить». Удалим таким же образом и график «скорость в/в введения» - ступенчатую функцию.
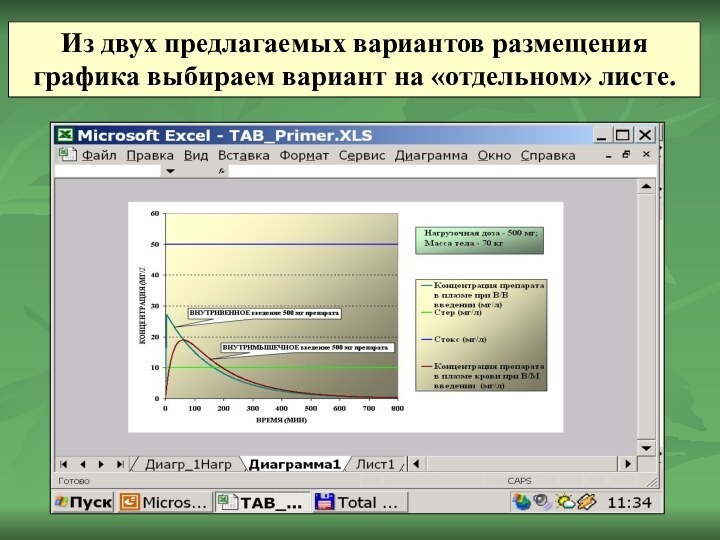
После этого на экране останутся 4 графика: две горизонтальные линии, отображающие терапевтическую и токсическую концентрации, характерные для конкретного препарата, и две кривые, отображающие изменение во времени концентрации препарата в плазме крови при В/В и В/М введении.
Слайд 50
Из двух предлагаемых вариантов размещения графика выбираем вариант
на «отдельном» листе.
Слайд 51
!!! На этом создание компьютерной реализации двух
фармакокинетических моделей - однокамерной (в/в введение препарата) и двухкамерной
(в/м введение) завершено.
В результате выполнения 1-го задания нами создан инструмент для осуществления индивидуального подбора режима дозирования конкретного препарата с учетом особенностей пациента - массы тела и состояния клиренса.
Продублируем построенный график и на каждом из двух построенных графиков оставим по одной кривой, соответствующей или внутривенному или внутримышечному введению препарата. Дадим имена каждому из двух листов с графиками (внутривенное или внутримышечное).
Слайд 53
Знания получаемые или закрепляемые на занятии
Понятие математической
модели реальной системы
Фармакокинетические понятия: (кажущийся объем распределения лекарственного вещества
в организме; общий клиренс; минимальные терапевтическая и токсическая концентрации; время полувыведения; нагрузочная и поддерживающая дозы лекарственного вещества)
Методика применения фундаментального закона сохранения вещества для вывода уравнений математических моделей для расчета концентрации лекарственного вещества в плазме крови при внутривенном или внутримышечном введении.
Методика осуществления компьютерной реализации математической модели фармакокинетики (средствами Microsoft Excel) для расчета меняющейся во времени концентрации лекарственного препарата в плазме крови после однократного внутривенного или внутримышечного введения заданной дозы этого вещества.