- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Мастер-класс Решение планиметрической задачи при подготовке к ЕГЭ по математике
Содержание
- 2. Определение внешнего угла треугольникаВнешний угол при вершине треугольника — это угол, смежный с углом .
- 3. Свойство внешнего угла треугольникаВнешний угол треугольника равен
- 4. В треугольнике АВС углы В и С равны 65
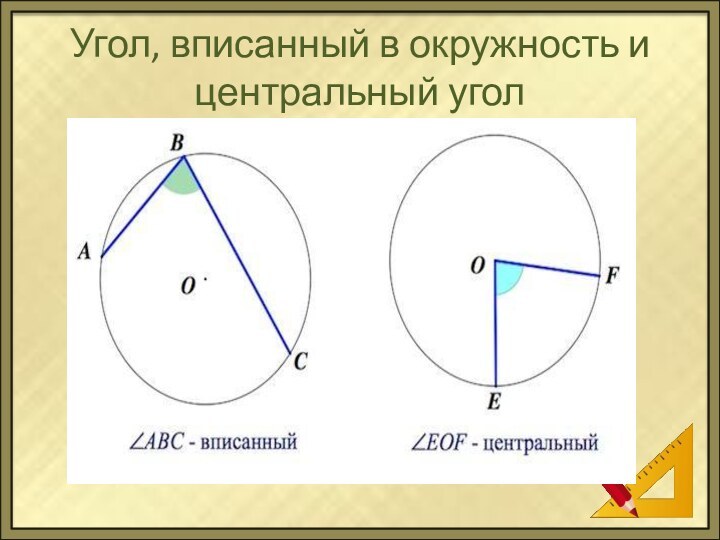
- 5. Угол, вписанный в окружность и центральный угол
- 6. Свойство углов, вписанных в окружность
- 7. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
- 8. Формулы для вычисления площади треугольника
- 9. Теорема синусов
- 10. Решить задачуТочка О — центр вписанной в
- 11. Решение задачи:а)O – центр вписанной в треугольник
- 12. O – центр вписанной в треугольник ABC
- 13. Скачать презентацию
- 14. Похожие презентации
Определение внешнего угла треугольникаВнешний угол при вершине треугольника — это угол, смежный с углом .








Слайд 2
Определение внешнего угла треугольника
Внешний угол при вершине треугольника —
это угол,
смежный с углом .
Слайд 3
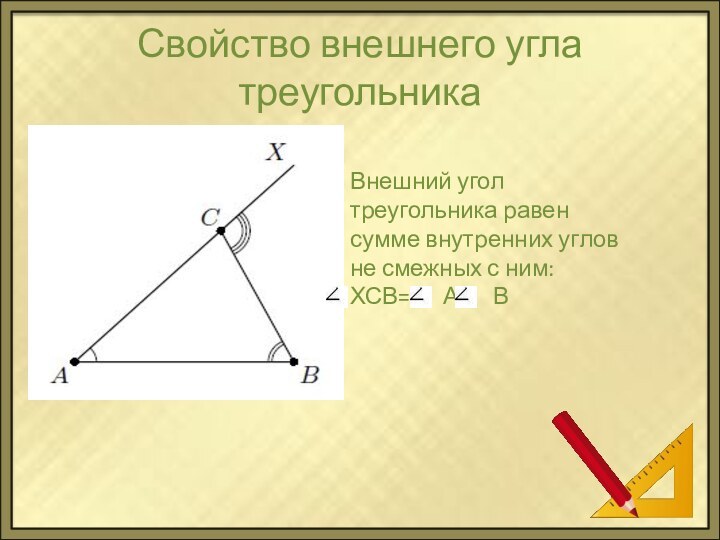
Свойство внешнего угла треугольника
Внешний угол треугольника равен сумме
внутренних углов не смежных с ним: ХСВ=
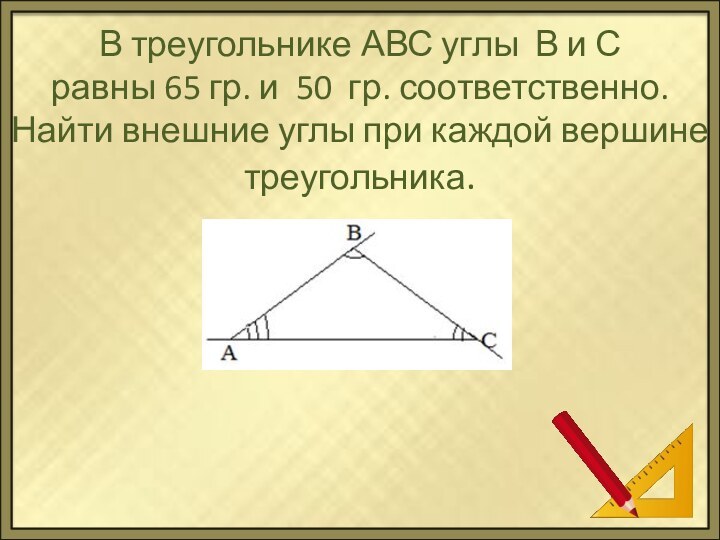
А+ ВСлайд 4 В треугольнике АВС углы В и С равны 65 гр. и 50 гр. соответственно. Найти
внешние углы при каждой вершине треугольника.
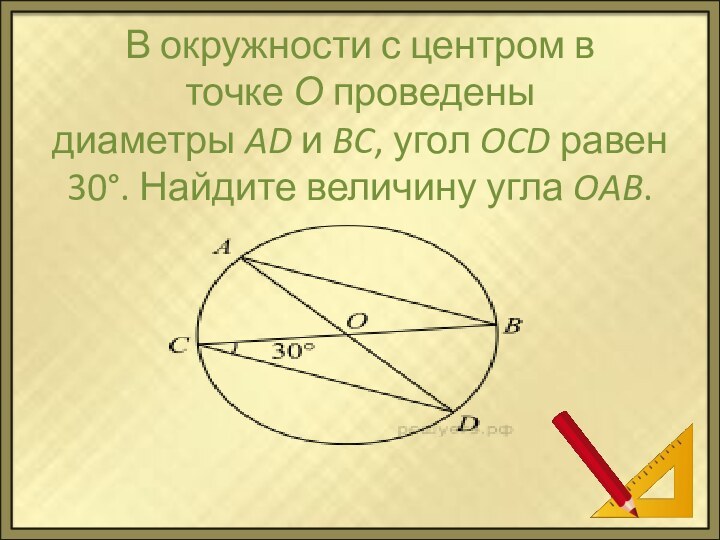
Слайд 7 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен
30°. Найдите величину угла OAB.
Слайд 10
Решить задачу
Точка О — центр вписанной в треугольник
ABC окружности. Прямая ВО вторично пересекает описанную около этого
треугольника окружность в точке Е.а) Докажите, что углы EOC = ECO.
б) Найдите площадь треугольника АСЕ, если радиус описанной около треугольника ABC окружности равен 6√3, угол ABC = 60°.
Слайд 11
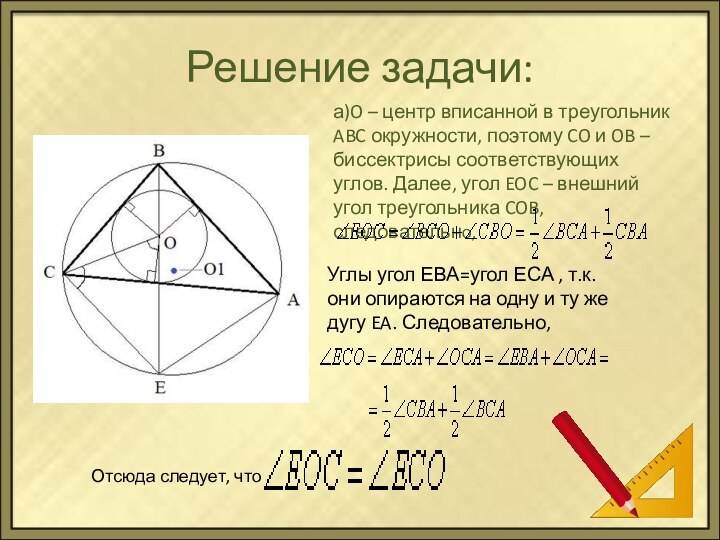
Решение задачи:
а)O – центр вписанной в треугольник ABC
окружности, поэтому CO и OB – биссектрисы соответствующих углов.
Далее, угол EOC – внешний угол треугольника COB, следовательно,Углы угол ЕВА=угол ЕСА , т.к. они опираются на одну и ту же дугу EA. Следовательно,
Отсюда следует, что
Слайд 12 O – центр вписанной в треугольник ABC окружности,
а O1 – центр описанной вокруг треугольника ABC окружности.
По условию радиус описанной окружности R=6√3. Так как угол АВС=60 гр. , то учитывая, что сумма противоположных углов четырехугольника вписанного в окружность, равна 180°, имеем:Т.к ВЕ- биссектриса угла В
Значит, дуги СЕ и ЕА равны, то СЕ=ЕА
Далее, так как треугольник BCE вписан в окружность с центром O1 и радиусом R=6√3, то по теореме синусов, имеем:





























