- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок учащихся ЕГЭ 2017
Содержание
- 2. Распоряжением правительства РФ от 24.12.2013 утверждена Концепция развития математического образования.
- 3. Минимальные порогиПрофильный уровень – 6 первичных балловБазовый уровень - 7 первичных баллов.
- 4. Общее количество участников ЕГЭ профильного уровня.2015 –
- 5. Не преодолели порог2016 год - 15, 33%2017
- 6. Задание 13.
- 7. Задание 14.Ненулевые баллы 6%.На рёбрах AB и
- 8. Задание 15.
- 9. Задание 16
- 10. Задание 17Ненулевые баллы 11%.В июле 2020 года
- 11. Задание 18
- 12. Задание 19Ненулевые баллы 4%.На доске написано 30
- 13. ИТОГИ ЕГЭнесформированность базовой логической культуры; • недостаточные
- 14. Рекомендациивыбор уровня экзамена, рекомендуя учащимся, которые неуверенно
- 15. РекомендацииДля учащихся, слабо овладевших или фактически не
- 16. Изменений в структуре КИМ ЕГЭ базового и профильного уровней в 2018 году не планируется.
- 17. Скачать презентацию
- 18. Похожие презентации
Распоряжением правительства РФ от 24.12.2013 утверждена Концепция развития математического образования.





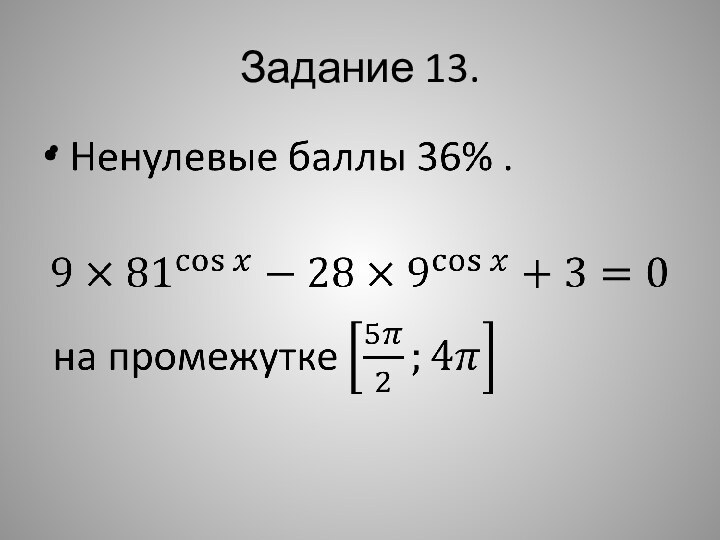











Слайд 2
Распоряжением правительства РФ от 24.12.2013 утверждена Концепция развития
математического образования.
Слайд 3
Минимальные пороги
Профильный уровень – 6 первичных баллов
Базовый уровень
- 7 первичных баллов.
Слайд 4
Общее количество участников ЕГЭ профильного уровня.
2015 – 521
121 чел.
2016 – 439 229 чел.
2017 – 390 981
чел.
Слайд 5
Не преодолели порог
2016 год - 15, 33%
2017 год
- 14,34%
100 баллов
2016 год – 296 чел.
2017 год –
224 чел.
Слайд 7
Задание 14.
Ненулевые баллы 6%.
На рёбрах AB и BC
треугольной пирамиды ABCD отмечены точки M и N соответственно,
причем AM:MB = CN:NB = 1:2. Точки P и Q середины ребер DA и DC соответственно.А) Докажите, что точки P, Q, M, N – лежат в одной плоскости
Б) Найдите отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Слайд 10
Задание 17
Ненулевые баллы 11%.
В июле 2020 года планируется
взять кредит в банке на некоторую сумму. Условия его
возврата таковы:— каждый январь долг увеличивается на % по сравнению с концом r % по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите . r
Слайд 12
Задание 19
Ненулевые баллы 4%.
На доске написано 30 различных
натуральных чисел, десятичная запись каждого из которых оканчивается или
на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?
б) Может ли ровно одно число на доске оканчиваться на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть на доске?





























