Слайд 2
Три пути ведут к знанию:
Путь размышления – это
путь самый благородный,
Путь подражания – это путь самый
легкий
И путь опыта – это путь самый горький.
Конфуций
Слайд 3
Повторим
Изучим
Узнаем
Проверим
Слайд 4
Квадратное уравнение – это…
Виды квадратных уравнений
Способы решения квадратных
уравнений
Слайд 5
Найди лишнее
2х2+4х-7=0
9х2-6х+9=0
5х2-2х=0
7х2+10х-9=0
Слайд 6
Найди лишнее
3х2-6х=0
-х2+9=0
2х2+5х=0
х2-6х-7=0
Слайд 7
Найди лишнее
х2-3х+4=0
-5х2-х+1=0
х2+6х+7=0
х2+5х+12=0
Слайд 8
Найди лишнее
х2+5х-7=0
2х2-6х+1=0
2х2-х+9=0
2х2+4х+5=0
Слайд 9
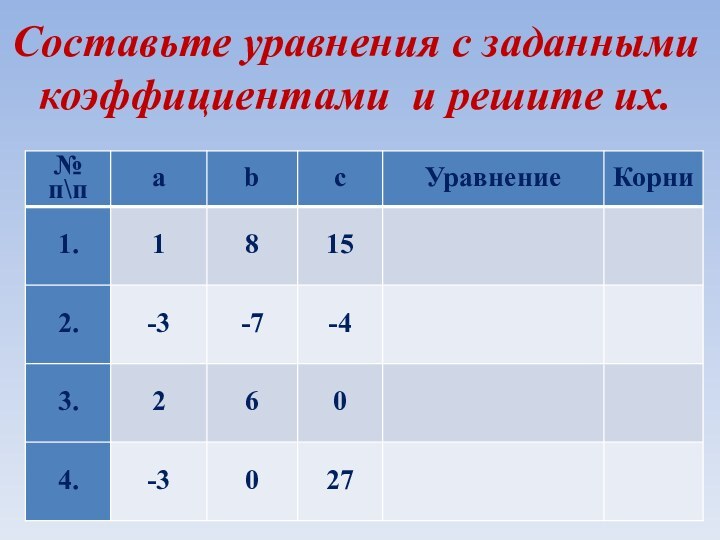
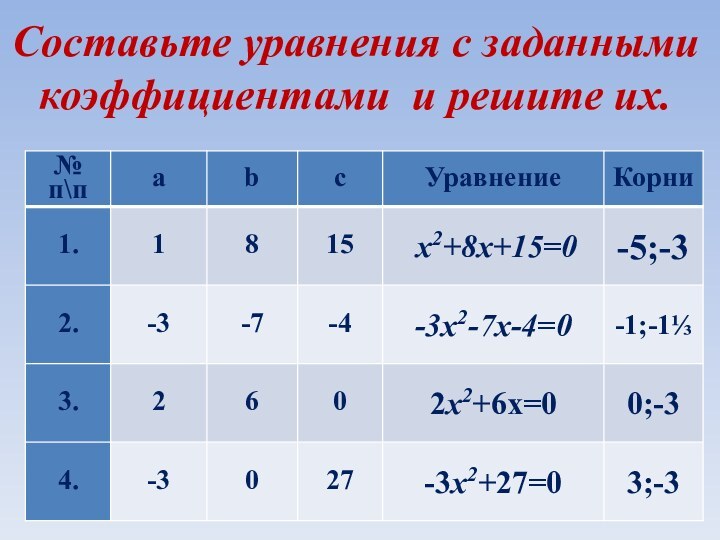
Составьте уравнения с заданными коэффициентами и решите их.
Слайд 10
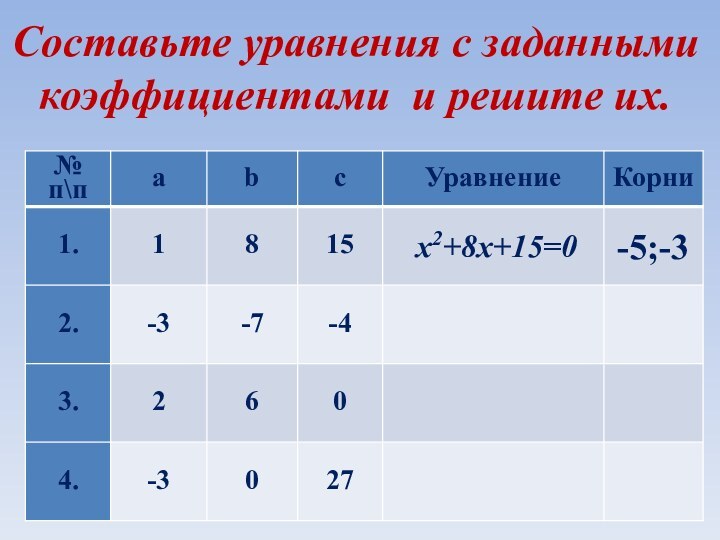
Составьте уравнения с заданными коэффициентами и решите их.
Слайд 11
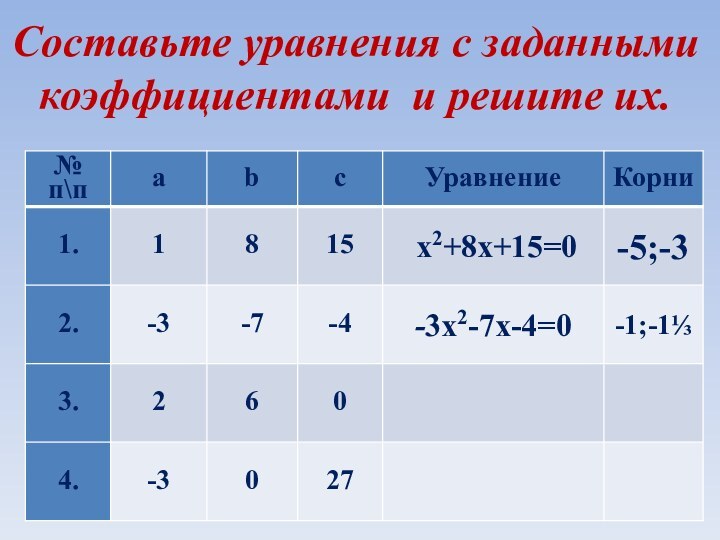
Составьте уравнения с заданными коэффициентами и решите их.
Слайд 12
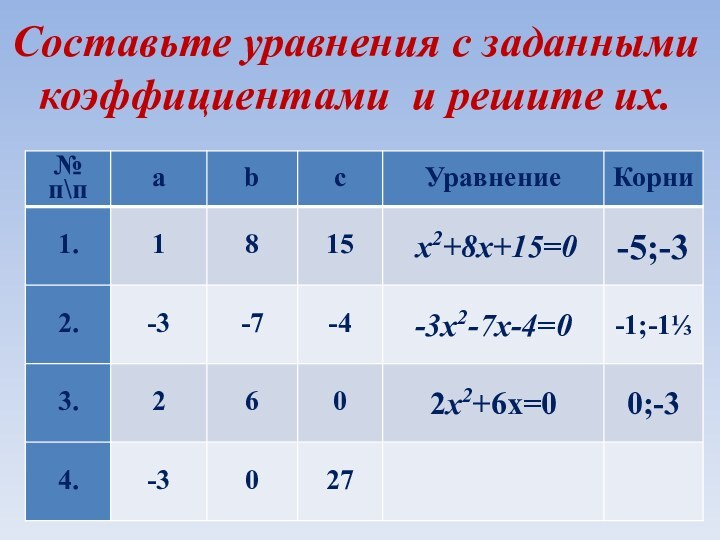
Составьте уравнения с заданными коэффициентами и решите их.
Слайд 13
Составьте уравнения с заданными коэффициентами и решите их.
Слайд 14
Историческая справка
«Кто хочет ограничиться настоящим без знания
прошлого, тот никогда его не поймет"
Лейбниц
Слайд 15
Обезьянок резвых стая
Всласть поевши, развлекалась.
Часть восьмая их
в квадрате
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая…
Сколько
ж было обезьянок,
Вы скажите, в этой стае?
Слайд 16
Способы решения квадратных уравнений, изучаемые в школе:
Разложение левой
части на множители
Метод выделения полного квадрата
С применением
формул корней квадратного уравнения
С применением теоремы Виета
Графический способ
Слайд 17
Нетрадиционные способы решения квадратных уравнений:
Способ переброски
По свойству
коэффициентов
С помощью циркуля и линейки
С помощью номограммы
Геометрический
Слайд 18
Свойство коэффициентов
Дано квадратное уравнение
ах2 + bх +
с = 0, где а ≠0.
Свойство 1.
Если а +
b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/а
Свойство 2.
Если а – b + с = 0, или b = а + с, то
х1 = – 1, х2 = – с/а
Слайд 19
Решите самостоятельно
(работа в парах):
Слайд 20
Способ «переброски»
ах2 + bх + с = 0, где а ≠ 0.
Умножая
обе его части на а, получаем уравнение а2х2 + аbх
+ ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0,равносильное данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х1 = у2/а.
Слайд 21
Решить уравнение способом «переброски»:
4Х2 +7Х + 3 =
0
У2 + 7У + 12 = 0
У1 = 3,
Х1 = 3/4
У2 = 4, Х2 = 1
Слайд 22
Практическая значимость КУ
Большинство практических задач реального мира сводится
к решению квадратных уравнений. Умение быстро, рационально и правильно
решать квадратные уравнения облегчает прохождение многих тем курса математики.
Слайд 23
Практическая значимость КУ
Туристы проплыли
на лодке против течения реки 6 км и по
озеру 15 км, затратив на путь по озеру на 1 час больше, чем на путь по реке.
Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.
Слайд 24
Квадратичная функция
Траектории струй воды
Параболы в архитектуре
Траектории прыжков животных
близки
к параболе
Слайд 25
Викторина «Дальше, дальше…»
1. Уравнение второй степени.
2. Сколько корней
имеет квадратное уравнение,
если D ˃ 0?
3. Равенство с
переменной?
4. От чего зависит количество корней квадратного уравнения?
5. Как называется квадратное уравнение, у которого первый коэффициент 1?
6. Сколько корней имеет квадратное уравнение,
если Д ˂ 0?
7. Что значит решить уравнение?
8. Есть у любого слова, у растения и может быть у уравнения?
Слайд 26
«Человеку, изучающему алгебру, часто полезнее решить одну и
ту же задачу тремя различными способами, чем решить три-четыре
различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».
У. Сойер
Слайд 27
Домашнее задание:
Подобрать нестандартную текстовую задачу, решаемую с помощью
квадратного уравнения, оформить ее с решением.