Слайд 2
Для составления таблицы истинности необходимо:
Выяснить количество строк (2n,
где n – количество переменных)
Выяснить количество столбцов (количество переменных
+ количество логических операций)
Построить таблицу, указывая названия столбцов и возможные наборы значений переменных
Заполнить таблицу истинности по столбцам
Слайд 3
Пример 1
Построим таблицу истинности для функции
F =
(А ∨ В) ∧ (¬A ∨ ¬B)
Переменных: две (А
и В), т.е. N = 2 ⇒ количество строк: 2n=22=4.
С заголовком: 5
Количество столбцов:
2 переменные + 5 операций (∨,∧,¬,∨ и ¬).
Итого: 7
Порядок операций:
1 5 2 4 3
F = (А ∨ В) ∧ (¬A ∨ ¬B)
Слайд 4
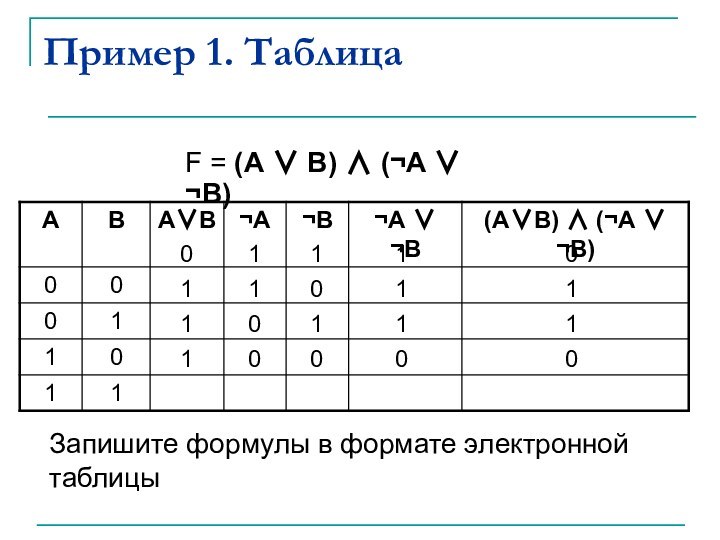
Пример 1. Таблица
0
1
1
1
1
1
0
0
F = (А ∨ В) ∧
(¬A ∨ ¬B)
1
0
1
0
1
1
1
0
0
1
1
0
Запишите формулы в формате электронной таблицы
Слайд 5
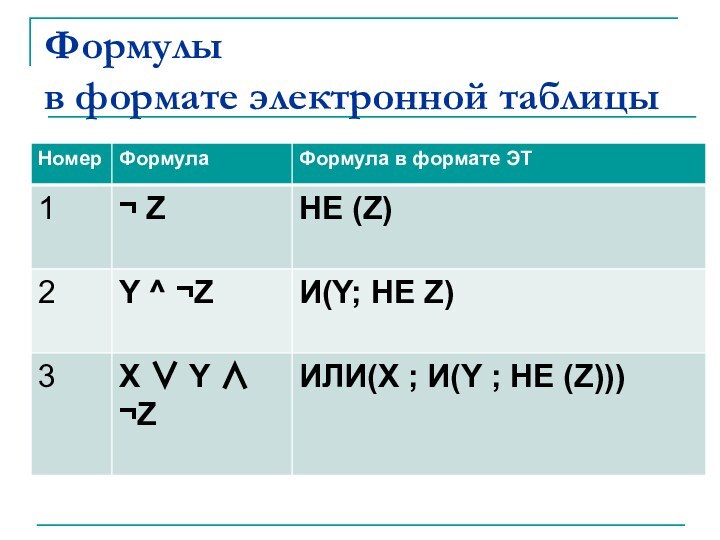
Формулы
в формате электронной таблицы
Слайд 6
Пример 2
Построим таблицу истинности для функции
F =
X ∨ Y ∧ ¬Z
Переменных: три (X, Y и
Z),
т.е. n = 3 ⇒ количество строк: 2n=23=8.
С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (∨,∧,¬).
Итого: 6
Порядок операций:
3 2 1
F = X ∨ Y ∧ ¬Z
Слайд 7
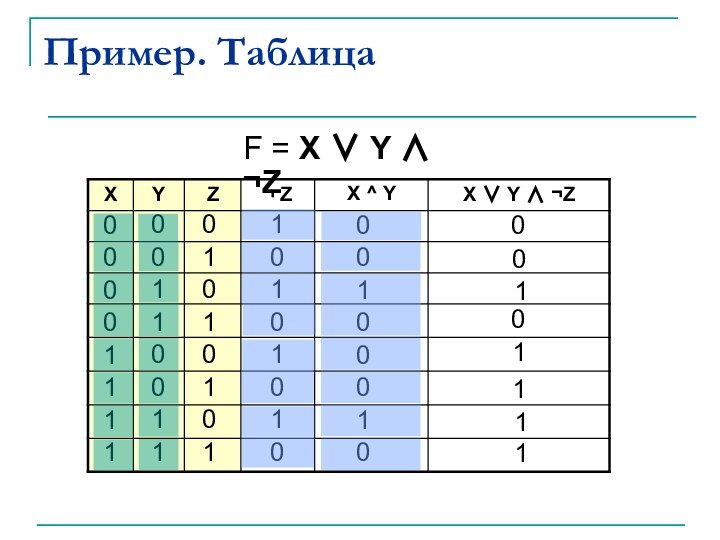
Пример. Таблица
0
0
0
0
1
1
1
1
F = X ∨ Y ∧ ¬Z
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
1
1
1
Слайд 8
Формулы
в формате электронной таблицы
Слайд 10
Сумматор
Алгебра логики дала в
руки конструктора мощное средство разработки, анализа и совершенствования логических
схем. Гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл математического моделирования.
Слайд 11
Схемные обозначения
С=f(вход1,
вход2)
С=f(вход1)
Слайд 12
Сумматор –
это электронная логическая схема, выполняющая суммирование
двоичных чисел.
В целях максимального упрощения работы компьютера
все многообразие математических операций в процессоре сводится к сложению двоичных чисел. Поэтому главной частью процессора является сумматор, который обеспечивает такое сложение. При сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в старший разряд. Обозначим слагаемые А и В, сумму S и перенос Р. Построим таблицу сложения одноразрядных двоичных чисел с учетом переноса в старший разряд.
Слайд 13
Сумматор –
Cоставим булево выражение по этой таблице:
_
_
S = A&B + A&B; P = A&B
Упростим формулу для S:
_ _ _ _
A&B = A&A +A&B = A&(A + B),
_ _ _ _
A&B = A & B +B&B = B&(A + B).
_ _ _ _
S = A&B + A&B = A&(A + B) + B&(A + B) =
_ _ ____
(A + B) &(A + B) = (A + B)&A&B.
Слайд 15
Триггер. Регистры
Триггер – устройство памяти компьютера для хранения
одного бита информации.
Это устройство позволяет запоминать, хранить и считывать
информацию. Триггер может находиться в одном из двух устойчивых состояний, которые соответствуют логической»1» и логическому «0». Триггер способен почти мгновенно переходить из одного электрического состояния в другое и наоборот.
Слайд 16
Триггер. Регистры
Самый распространенный триггер – SR-триггер ( S
и R от английских слов set – установка, reset
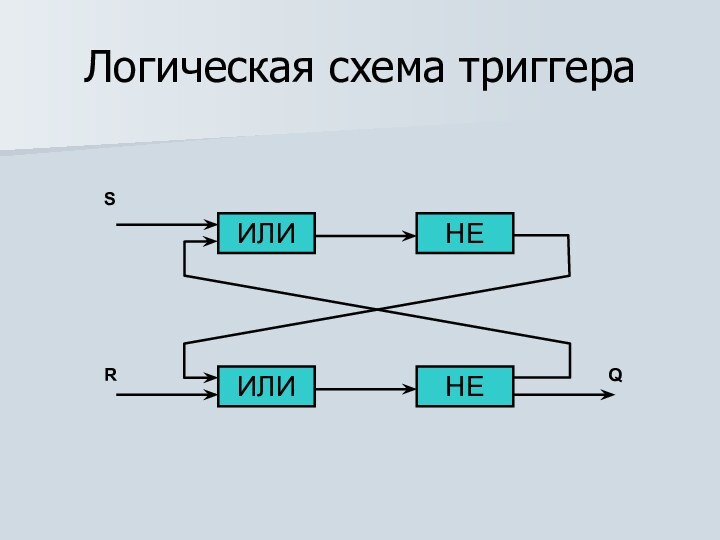
– сброс). Он имеет два входа S и R, два выхода Q и ¬Q. На каждый из входов подаются входные сигналы в виде кратковременных импульсов «1», отсутствие импульса – «0».
Для построения триггера достаточно двух логических элементов «ИЛИ» и двух элементов «НЕ».
Слайд 17
Регистр
Регистр - это устройство, предназначенное для хранения
многоразрядного двоичного числового кода, которым можно представлять и адрес,
и команду, и данные. Если в регистр входит N триггеров, то можно запомнить N бит информации. Регистры содержатся в различных вычислительных узлах компьютера – процессоре, периферийных устройствах и т.д.
Слайд 18
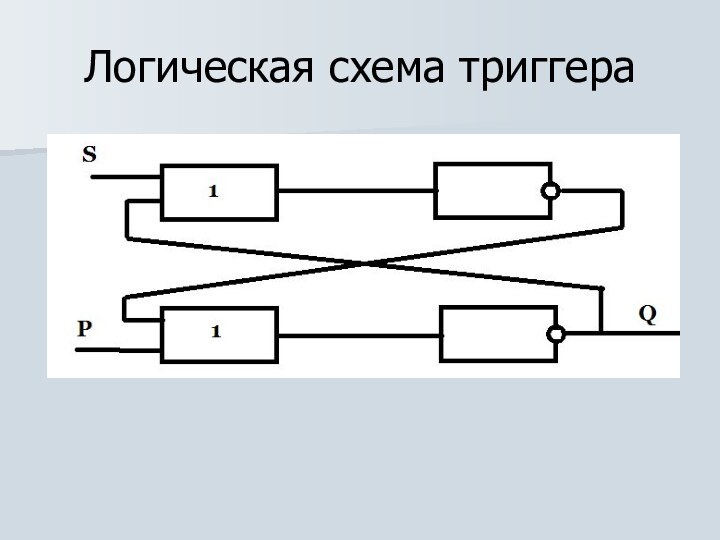
Логическая схема триггера
ИЛИ
ИЛИ
НЕ
НЕ
S
R
Q
Слайд 20
Триггер
При подаче сигнала на вход S триггер переходит
в устойчивое единичное состояние.
При подаче сигнала на вход R
триггер сбрасывается в устойчивое нулевое состояние.
Слайд 21
Триггер
При отсутствии входных сигналов триггер сохраняет тот сигнал,
который был установлен входным импульсом.
Если на два входа подан
сигнал, то появляется неоднозначный результат, поэтому такая комбинация запрещена.