Слайд 2
Одаренный ребенок – это ребенок, который выделяется яркими,
очевидными, иногда выдающимися достижениями (или имеет внутренние предпосылки для
таких достижений) в том или ином виде деятельности.
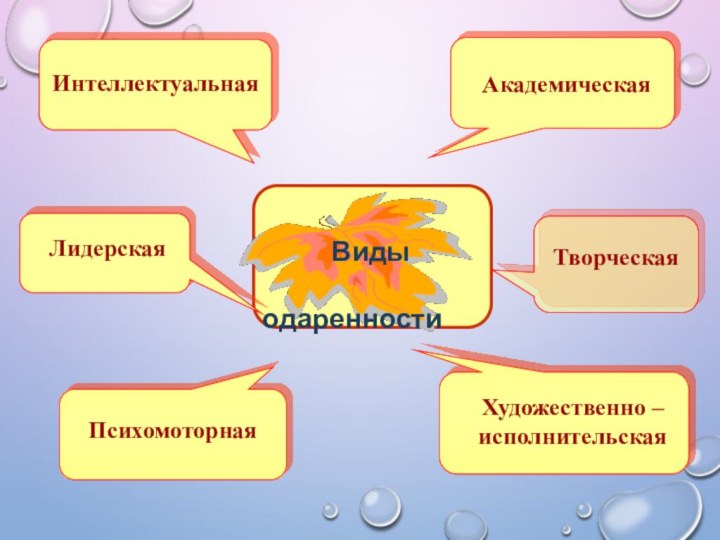
Три категории одаренных детей:
Дети с необыкновенно высоким общим уровнем умственного развития (такие дети чаще всего встречаются в дошкольном и младшем школьном возрасте).
Дети с признаками специальной умственной одаренности – в определенной области науки (подростковый образ).
Учащиеся, не достигающие по каким-либо причинам успехов в учении, но обладающие яркой познавательной активностью, оригинальностью психического склада, незаурядными умственными резервами (чаще встречаются в старшем школьном возрасте).
Слайд 4
.
Признаки наличия математических
способностей у ребенка
Быстрое
овладение математическими знаниями, умениями и навыками.
Быстрота понимания объяснения
учителя.
Логичность, самостоятельность мышления.
Находчивость и сообразительность при изучении математики.
Быстрое и прочное запоминание материала.
Высокая степень развития способности к обобщению, анализу и синтезу математического материала.
Пониженная утомляемость при занятиях математикой.
Способность быстро переключаться с прямого на обратный ход мысли.
Слайд 5
Можно условно выделить несколько групп детей с учётом

уровня и характера их мотивации. Это помогает в выборе
приемов педагогической поддержки.
1)»Мотивация на результат» (такие дети не умеют радоваться успехам других, болезненно переживают свои неудачи и готовы «расталкивать всех локтями» для достижения цели; здесь необходима индивидуальная работа психолога)
2)»Мотивация на самоутверждение» (их психологическая защита строится на тезисе «скучно, неинтересно», они также не любят успехов других, но они способны признавать высокий профессионализм педагога; основной прием поддержки в данной ситуации «косвенная аналогия», создание ситуаций, где ученик смог бы увидеть себя)
3)»Мотивация на творчество» (такие дети не любят фактической стороны учения, но могут выдавать нестандартные идеи и мысли; для подобных детей необходимо обучение самоконтролю, самоорганизации)
4)»Мотивация на познание» (такие дети требуют индивидуальной программы обучения; задача педагога-наставника не «культивировать» свой предмет, а помочь ученику увидеть и понять картину мира, понять значимость интегрального знания
Слайд 6
Целью обучения математики в школе является
не только овладение конкретными математическими знаниями, но и интеллектуальное
развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для продуктивной жизни в обществе. В настоящий момент образование характеризуется как процесс обучения и воспитания в интересах личности, общества и государства, направленный на развитие индивида, его индивидуальных, умственных и физических способностей, одаренности и таланта.
Слайд 7
Анализ учебников математики показывает, что не
один из учебников не содержит необходимого набора задач, направленных
на развитие одаренных учащихся, т.е. задач на развитие различных познавательных процессов, обеспечивающих достижение целей развития способных детей. Современные образовательные стандарты, программы математического образования для общеобразовательной школы лишь отмечают развивающие возможности математики, но не уделяют внимания их использованию для развития одаренных детей в процессе обучения.
Слайд 8
Формы работы с одаренными учащимися
творческие мастерские;
групповые занятия по
параллелям классов с сильными учащимися;
факультативы;
кружки по интересам;
занятия исследовательской деятельностью;
конкурсы;
интеллектуальный
марафон;
научно-практические конференции;
участие в олимпиадах;
работа по индивидуальным планам;
сотрудничество с другими школами, ВУЗами.
Слайд 9
Примеры задач, используемых на занятиях кружка
Слайд 10
Акробат и собачонка весят два пустых бочонка. Шустрый
пес без акробата Весит два мотка шпагата. А с
одним мотком ягненок Весит - видите - бочонок. Сколько весит акробат в пересчете на ягнят?
Слайд 11
Задача на развитие
логического мышления
Жили-были две фигуры: Круг и
Квадрат. На их улице было 3 дома: один дом
был с окном и трубой, другой с окном, но без трубы, третий с трубой, но без окна. Каждая фигура жила в своем доме. Круг и квадрат жили в домах с окнами. Квадрат любил тепло и часто топил печку. Кто в каком доме жил?
Слайд 12
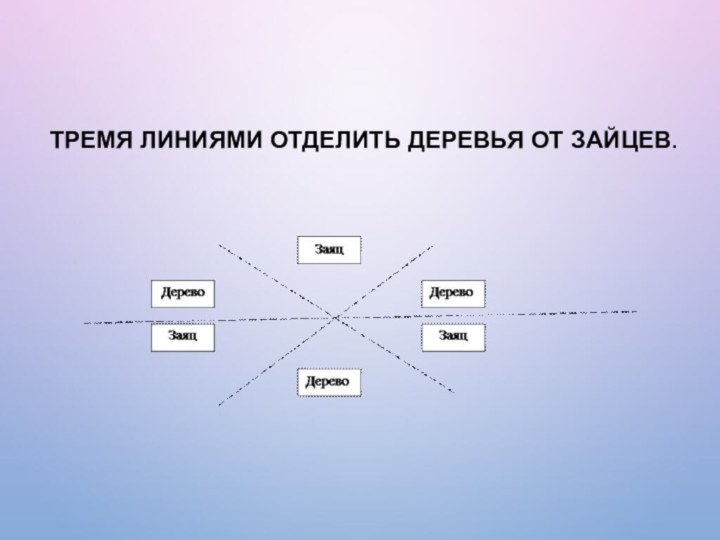
Тремя линиями отделить деревья от зайцев.
Слайд 13
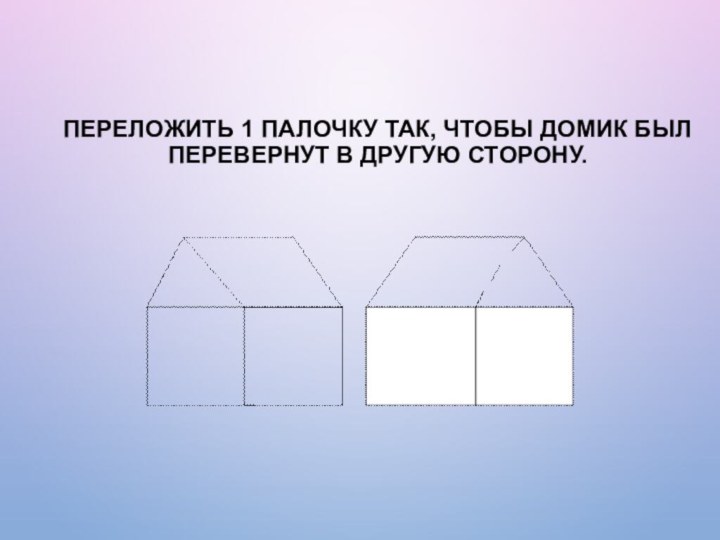
Переложить 1 палочку так, чтобы домик был перевернут
в другую сторону.
Слайд 14
Занимательные вопросы
Сколько ушей у трёх мышей?
Сколько лап у
двух медвежат?
У семи братьев по одной сестре. Сколько всего
сестёр?
У бабушки Даши внучка Маша, кот Пушок и собака Дружок. Сколько всего внуков у бабушки?
Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей!
Горело 7 свечей. 2 свечи погасили, а остальные продолжали гореть. Сколько свечей осталось? (2, остальные сгорели).
В корзине три яблока. Как поделить их между тремя детьми так, чтобы одно яблоко осталось в корзине? (Отдать одно яблоко вместе с корзиной).
На берёзе три толстых ветки, на каждой толстой ветке по три тоненьких веточки. На каждой тоненькой веточке по одному яблочку. Сколько всего яблок? (Нисколько – на берёзе яблоки не растут.)
Слайд 15
Задачи-шутки
На столе три стакана с ягодами. Вова съел
один стакан ягод. Сколько стаканов осталось на столе? (Три)
Шли
двое, остановились, один у другого спрашивает: «Это черная?». – «Нет, это красная». – «А почему она белая?» – «Потому, что зеленая». О чем они вели разговор? (О смородине)
На столе лежат два апельсина и четыре банана. Сколько овощей на столе? (Нисколько)
На груше росло десять груш, а на иве на две груши меньше. Сколько груш росло на иве? (Нисколько)
На какое дерево сядет воробей после дождя? (На мокрое)
Чего больше в квартире: стульев или мебели? (Мебели)
Ты да я да мы с тобой. Сколько нас всего? (Два)
Как можно сорвать ветку, не спугнув на ней птичку? (Нельзя, улетит).
Слайд 16
Задачи в стихах
Решила старушка ватрушки испечь.
Поставила
тесто да печь затопила.
Решила старушка ватрушки испечь,
А сколько их
надо — совсем позабыла.
Две штучки — для внучки,
Две штучки — для деда,
Две штучки — для Тани,
Дочурки соседа... Считала, считала, да сбилась,
А печь-то совсем протопилась!
Помоги старушке сосчитать ватрушки
(В. Кудрявцева)
Слайд 17
Целью кружковой работы является не только овладение учащимися
умениями и навыками, но развитие в детях математических способностей,
различных качества ума, вычислительной культуры, элементов творческой деятельности, научного мировоззрения.
Слайд 18
Помощь одаренным учащимся в самореализации их творческой направленности
создание
для ученика ситуации успеха и уверенности, через индивидуальное обучение
и воспитание;
организация научно-исследовательской деятельности;
организация и участие в интеллектуальных играх, творческих конкурсах, предметных олимпиадах, научно-практических конференциях.
разработка и реализация межпредметных научно-исследовательских проектов.
изготовление компьютерных презентаций, видеороликов, исследований.
Слайд 19
Поощрение одаренных детей
Публикация в СМИ
Публикация на сайте школы
Награждение
Слайд 20
Рекомендации учителям в работе с одаренными детьми
Учителю не
следует уделять слишком много внимания
игровому
обучению с ярко выраженным элементом соревнования. Одаренный ребенок будет чаще
всего оказываться победителем, что может вызвать
неприязнь соучеников и не благоприятствует созданию атмосферы всеобщей заинтересованности, к которой
стремится учитель.
Учитель не должен возводить одаренного ребенка на
пьедестал или делать из него вундеркинда в глазах других учеников. Успехи его будут должным образом оценены, а неуместное выпячивание его исключительности достижений рождает чаще всего раздражение, ревность и отторжение вместо ожидаемой похвалы. Другая крайность — преднамеренное публичное принижение уникальных способностей и даже сарказм со стороны учителя,— конечно, недопустима.