Слайд 2
Маршруты. Циклы. Связность графов
Отдельные свойства связных графов –
их эйлеровость и гамильтоновость («ость» считаем допустимым элементом словообразования).
Граф
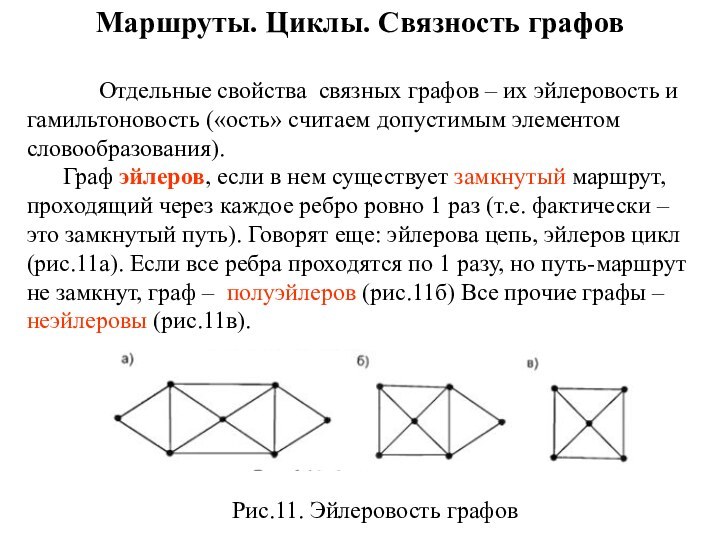
эйлеров, если в нем существует замкнутый маршрут, проходящий через каждое ребро ровно 1 раз (т.е. фактически – это замкнутый путь). Говорят еще: эйлерова цепь, эйлеров цикл (рис.11а). Если все ребра проходятся по 1 разу, но путь-маршрут не замкнут, граф – полуэйлеров (рис.11б) Все прочие графы – неэйлеровы (рис.11в).
Рис.11. Эйлеровость графов
Слайд 3
Маршруты. Циклы. Связность графов
Эйлеров граф – это граф,
в котором существует цикл, содержащий все ребра графа по
одному разу (вершины могут повторяться).
Эйлерова цепь (Эйлеров цикл) – это цепь (цикл), которая содержит все ребра графа (вершины могут повторяться).
Слайд 4
Маршруты. Циклы. Связность графов
Гамильтоновость, полугамильтоновость, негамильтоновость графа определяются
аналогично, но речь идет о неповторяемости и однократной проходимости
вершин, а не ребер (рис.12).
Рис.12. Гамильтоновость графов: полная (а), полу- (б), не- (в)
Слайд 5
Маршруты. Циклы. Связность графов
Гамильтонов граф – граф, в
котором есть гамильтонов цикл.
Гамильтонов путь – простой путь в
графе, содержащий все вершины графа ровно по одному разу.
Гамильтонов цикл – простой цикл в графе, содержащий все вершины графа ровно по одному разу.
Слайд 6
Маршруты. Циклы. Связность графов
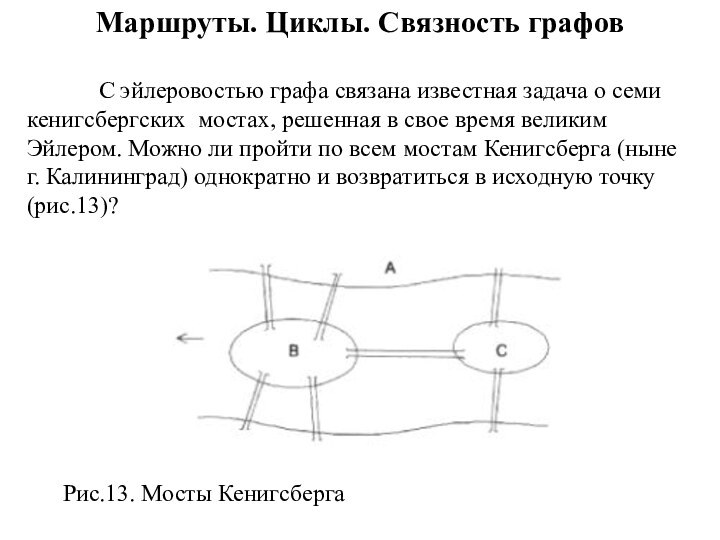
С эйлеровостью графа связана известная
задача о семи кенигсбергских мостах, решенная в свое время
великим Эйлером. Можно ли пройти по всем мостам Кенигсберга (ныне г. Калининград) однократно и возвратиться в исходную точку (рис.13)?
Рис.13. Мосты Кенигсберга
Слайд 7
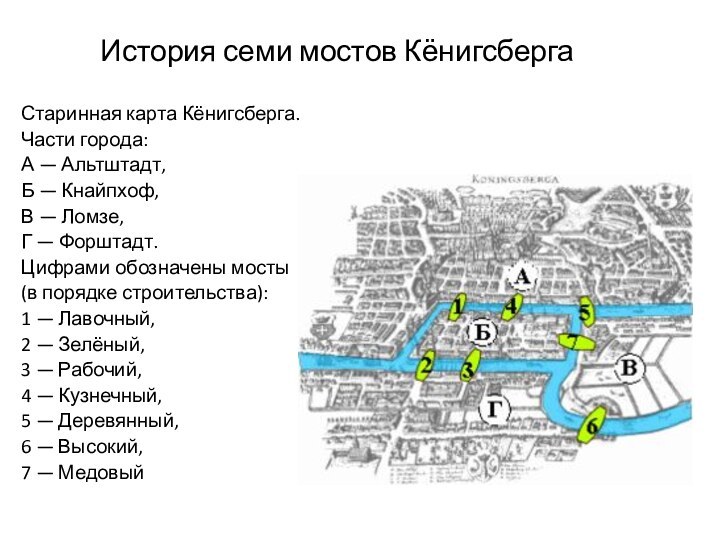
История семи мостов Кёнигсберга
Старинная карта Кёнигсберга.
Части
города:
А — Альтштадт,
Б — Кнайпхоф,
В — Ломзе,
Г — Форштадт.
Цифрами обозначены мосты
(в порядке строительства):
1 — Лавочный,
2 — Зелёный,
3 — Рабочий,
4 — Кузнечный,
5 — Деревянный,
6 — Высокий,
7 — Медовый
Слайд 8
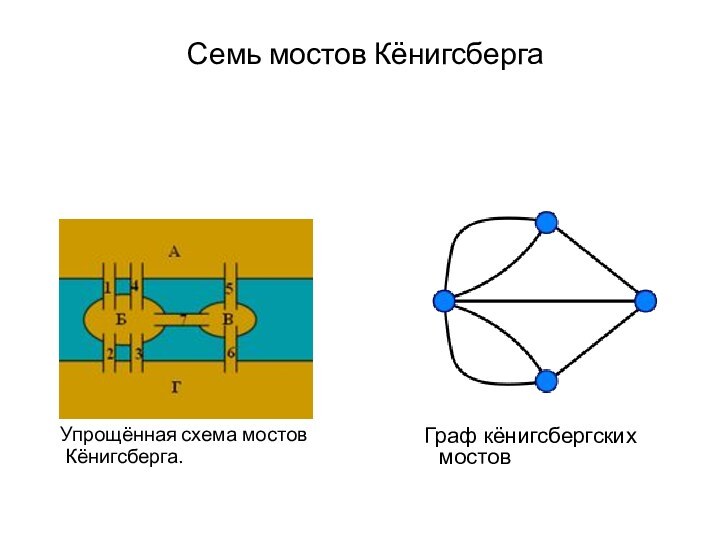
Семь мостов Кёнигсберга
Упрощённая схема мостов
Кёнигсберга.
Граф кёнигсбергских мостов
Слайд 9
Выводы Эйлера
Число нечётных вершин (вершин, к которым ведёт
нечётное число рёбер) графа всегда чётно. Невозможно начертить граф,
который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Леонард Эйлер
1707-1783
Слайд 10
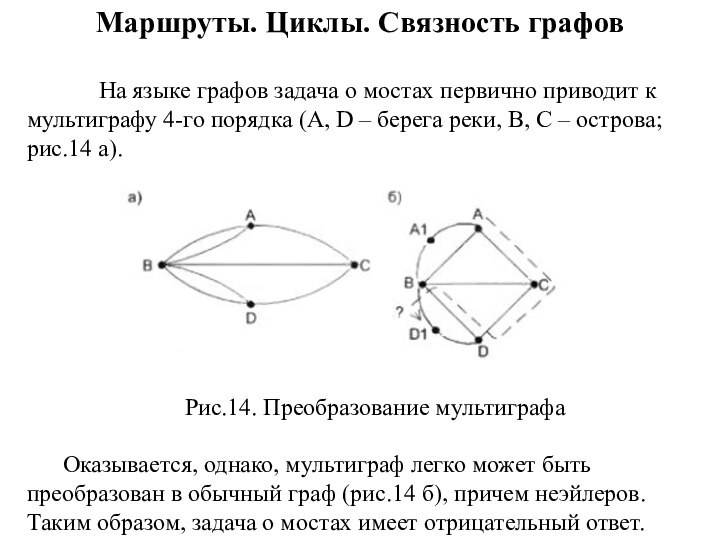
Маршруты. Циклы. Связность графов
На языке графов задача о
мостах первично приводит к мультиграфу 4-го порядка (A, D
– берега реки, В, С – острова; рис.14 а).
Рис.14. Преобразование мультиграфа
Оказывается, однако, мультиграф легко может быть преобразован в обычный граф (рис.14 б), причем неэйлеров. Таким образом, задача о мостах имеет отрицательный ответ.
Слайд 11
Планарные графы
Планарный граф может быть изображен на плоскости
без пересечения ребер. Такое изображение – карта графа. Карта
связная, если планарный граф связный.
Область карты графа – часть плоскости, ограниченная контуром из ребер. Степень области – количество ребер, составляющих границу области.
Рис.15. Планарные графы и их области
Все четыре области графа рис.15а – треугольные, Dr = 3.
В графе рис.15б область 2 имеет степень 4, а внутренняя область 1 – степень 6, поскольку ребро, ориентированное внутрь этой области, проходится дважды.
Слайд 12
Планарные графы
Теорема о сумме степеней
всех областей планарного графа может быть,
даже и несвязного):
т.е. сумма эта равна удвоенному количеству ребер.
Доказательство аналогично соответствующему доказательству теоремы о сумме степеней всех вершин: каждое ребро учитывается в этой сумме дважды, поскольку входит в граничный контур двух смежных областей или является «внутренним».
Слайд 13
Планарные графы
Теорема Эйлера для связных планарных графов:
⏐W⏐– ⏐L⏐+
⏐R⏐=E = 2,
т.е. количество вершин минус количество ребер
плюс количество областей есть величина постоянная (константа Эйлера Е), имеющая значение 2.
Например, для графа рис.15а сумма степеней 4 областей равна 3*4 = 12, а ребер 6.
В графе рис.15б сумма 6 + 4 = 10, и ребер – 5.
Слайд 14
Планарные графы
Доказательство теоремы ведется с использованием своеобразной индукции.
Для тривиального графа (первого порядка) |W| = 1, |L|
= 0, |R| = 1 теорема справедлива.
Любой другой планарный граф получается из этого тривиального выполнением в любой последовательности всего двух операций:
добавление вершины;
добавление ребра.
Слайд 15
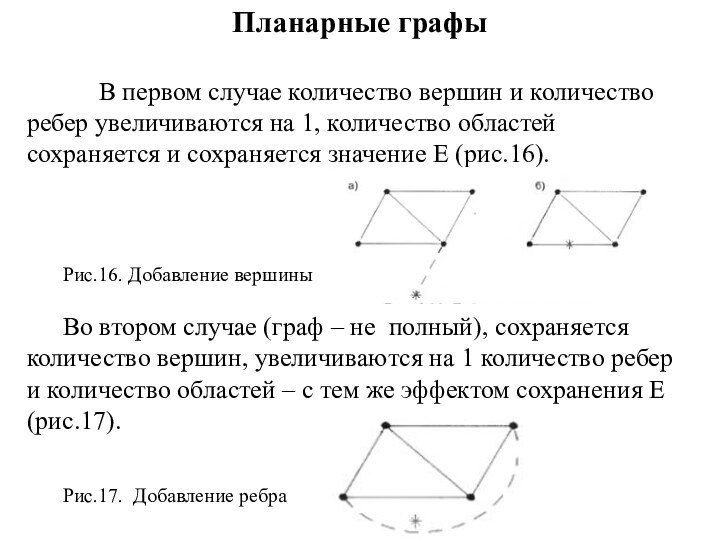
Планарные графы
В первом случае количество вершин и количество
ребер увеличиваются на 1, количество областей сохраняется и сохраняется
значение Е (рис.16).
Рис.16. Добавление вершины
Во втором случае (граф – не полный), сохраняется количество вершин, увеличиваются на 1 количество ребер и количество областей – с тем же эффектом сохранения Е (рис.17).
Рис.17. Добавление ребра
Слайд 16
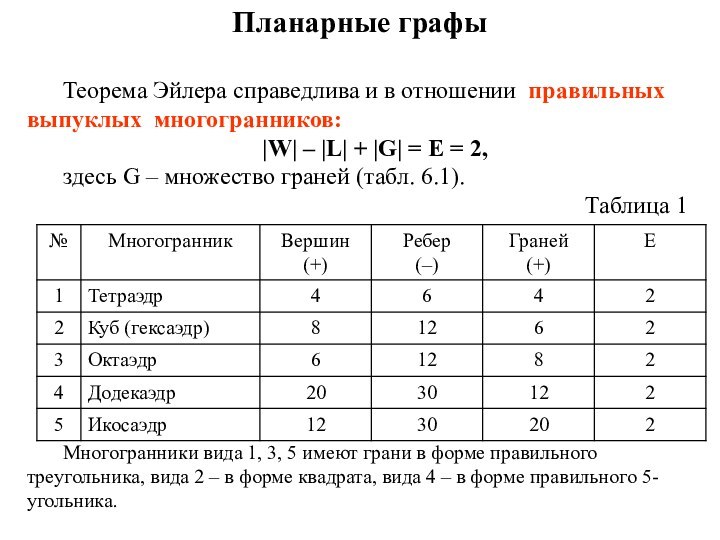
Планарные графы
Теорема Эйлера справедлива и в отношении правильных
выпуклых многогранников:
|W| – |L| + |G| = Е =
2,
здесь G – множество граней (табл. 6.1).
Таблица 1
Многогранники вида 1, 3, 5 имеют грани в форме правильного треугольника, вида 2 – в форме квадрата, вида 4 – в форме правильного 5-угольника.
Слайд 17
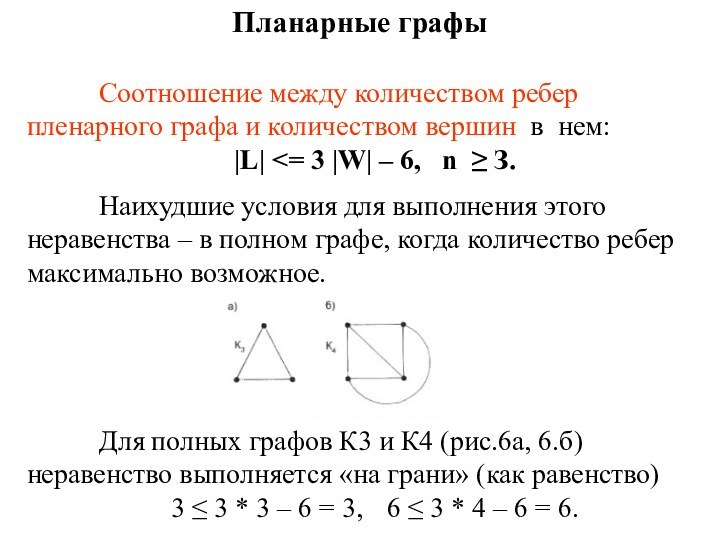
Планарные графы
Соотношение между количеством ребер пленарного графа и
количеством вершин в нем:
|L|
n ≥ З.
Наихудшие условия для выполнения этого неравенства – в полном графе, когда количество ребер максимально возможное.
Для полных графов К3 и К4 (рис.6а, 6.б) неравенство выполняется «на грани» (как равенство)
3 ≤ 3 * 3 – 6 = 3, 6 ≤ 3 * 4 – 6 = 6.
Слайд 18
Планарные графы
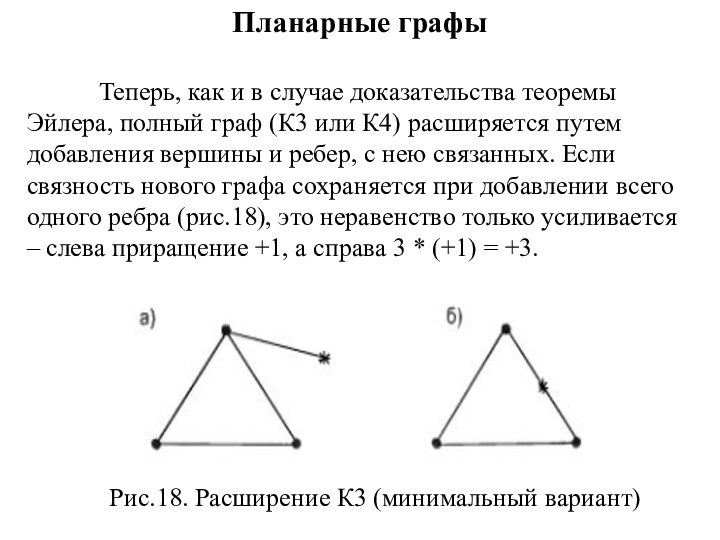
Теперь, как и в случае доказательства теоремы
Эйлера, полный граф (К3 или К4) расширяется путем добавления
вершины и ребер, с нею связанных. Если связность нового графа сохраняется при добавлении всего одного ребра (рис.18), это неравенство только усиливается – слева приращение +1, а справа 3 * (+1) = +3.
Рис.18. Расширение К3 (минимальный вариант)
Слайд 19
Планарные графы
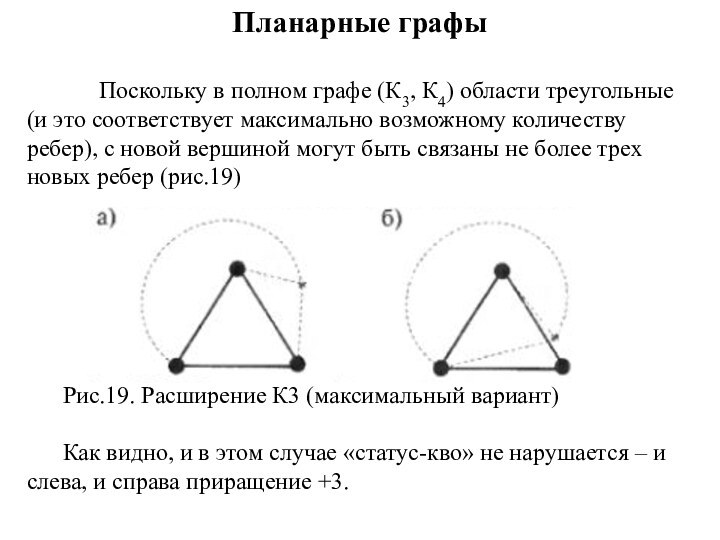
Поскольку в полном графе (К3, К4) области
треугольные (и это соответствует максимально возможному количеству ребер), с
новой вершиной могут быть связаны не более трех новых ребер (рис.19)
Рис.19. Расширение К3 (максимальный вариант)
Как видно, и в этом случае «статус-кво» не нарушается – и слева, и справа приращение +3.
Слайд 20
Планарные графы
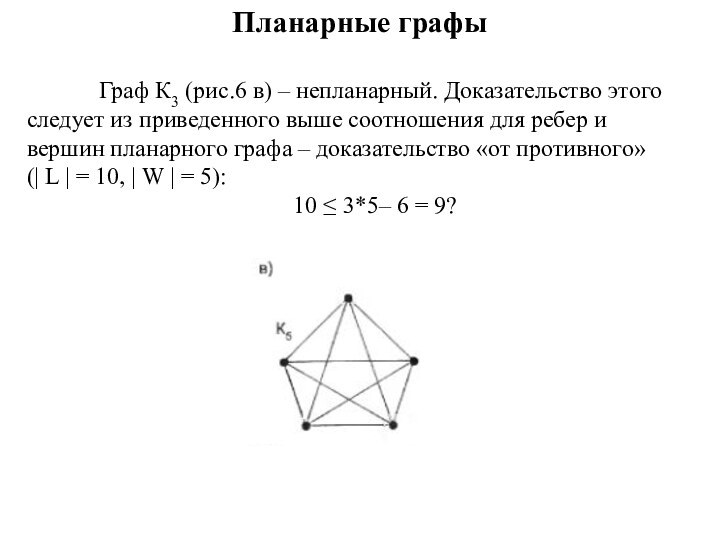
Граф К3 (рис.6 в) – непланарный. Доказательство
этого следует из приведенного выше соотношения для ребер и
вершин планарного графа – доказательство «от противного» (| L | = 10, | W | = 5):
10 ≤ 3*5– 6 = 9?
Слайд 21
Планарные графы
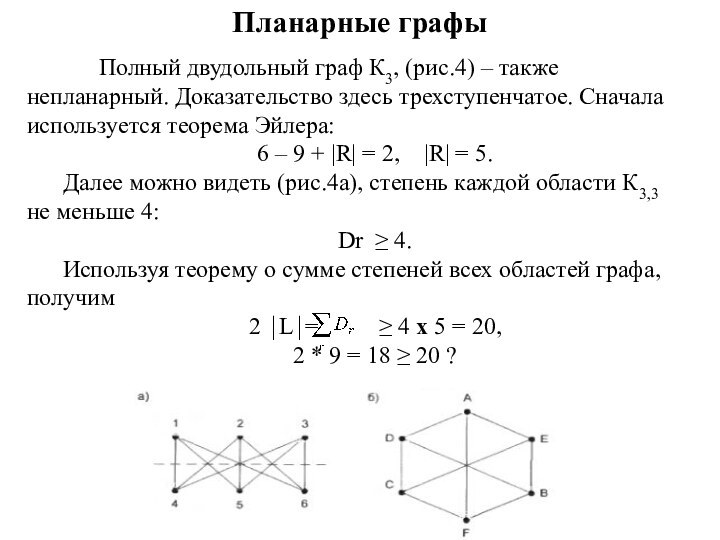
Полный двудольный граф К3, (рис.4) – также
непланарный. Доказательство здесь трехступенчатое. Сначала используется теорема Эйлера:
6 –
9 + |R| = 2, |R| = 5.
Далее можно видеть (рис.4а), степень каждой области К3,3 не меньше 4:
Dr ≥ 4.
Используя теорему о сумме степеней всех областей графа, получим
2 ⏐L⏐= ≥ 4 х 5 = 20,
2 * 9 = 18 ≥ 20 ?
Слайд 22
Планарные графы
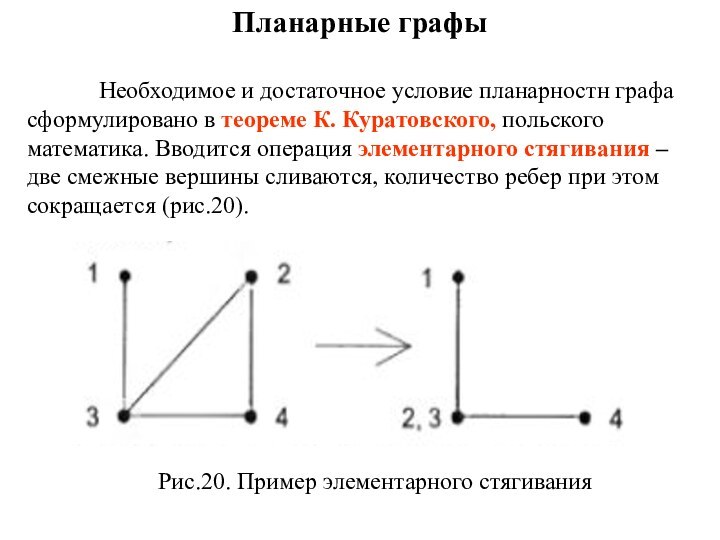
Необходимое и достаточное условие планарностн графа сформулировано
в теореме К. Куратовского, польского математика. Вводится операция элементарного
стягивания – две смежные вершины сливаются, количество ребер при этом сокращается (рис.20).
Рис.20. Пример элементарного стягивания
Слайд 23
Планарные графы
Теорема Куратовского утверждает:
граф планарный тогда и
только тогда, когда в процессе выполнения операций элементарного стягивания
он не содержит подграфов вида К5 и К3,3
В теории вероятностей исчерпывающая характеристика случайной величины – ее закон распределения вероятностей, очень емкая форма.
В практических же задачах часто достаточно числовых характеристик распределения. Так и у графов.
Наряду с однозначным описанием графа – матрицей смежности – актуальны так называемые числа графа.
Одним из них является хроматическое число.
Слайд 24
Планарные графы
Речь идет о раскраске графа.
Раскрашиваться могут
вершины, ребра и области. Необходимое условие – смежные элементы
должны иметь разный цвет Обычно имеются в виду вершины графа Хроматическое число графа (χ, «хи») – это минимально необходимое число красок для окрашивания вершин графа.
Для планарных графов на рис.21 это чисто составляет соответственно 2, 3 и 4 (цифрами указан цвет вершины, «номер» цвета).
Рис. 21. Раскрашивание вершин графа
Слайд 25
Планарные графы
Теорема о четырех красках утверждает, что для
пленарного связного графа значение хроматического числа не превышает 4.
Теорема
эта считается до сих пор недоказанной.
Слайд 26
Проблема четырех красок
Проблема четырёх красок — математическая задача,
предложенная Гатри (англ.) в 1852 году.
Выяснить, можно ли всякую
расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, чтобы все стороны каждого треугольника были раскрашены в разные цвета.
Слайд 27
Планарные графы
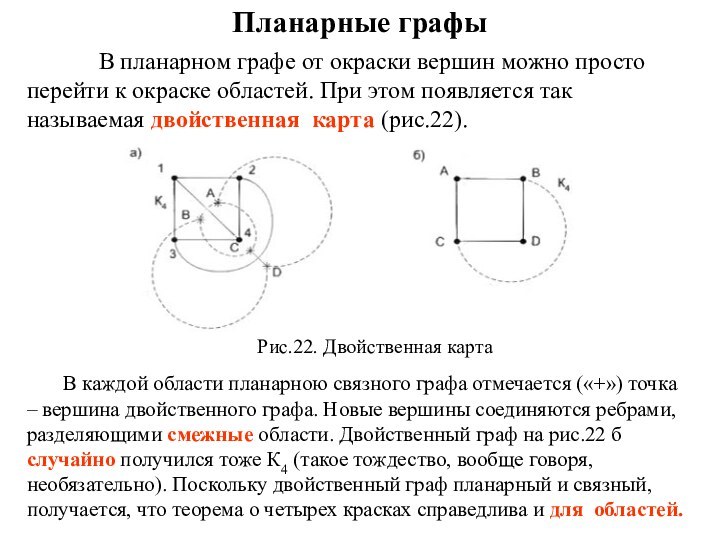
В планарном графе от окраски вершин можно
просто перейти к окраске областей. При этом появляется так
называемая двойственная карта (рис.22).
Рис.22. Двойственная карта
В каждой области планарною связного графа отмечается («+») точка – вершина двойственного графа. Новые вершины соединяются ребрами, разделяющими смежные области. Двойственный граф на рис.22 б случайно получился тоже К4 (такое тождество, вообще говоря, необязательно). Поскольку двойственный граф планарный и связный, получается, что теорема о четырех красках справедлива и для областей.
Слайд 28
Ориентированные графы (орграфы)
Можно отметить два существенных отличия орграфов
от обычных графов:
ориентация ребер, которые становятся дугами (дуга –
«ребро со стрелкой»);
наличие петель (рис.23).
Рис.23. Орграф
Слайд 29
Ориентированные графы (орграфы)
Как и обычные графы, орграфы однозначно
описываются их матрицами смежности.
Для орграфа рис.23:
МS* =
Видно,
что матрица смежности менее насыщена единицами.
В общем случае она несимметрична относительно главной диагонали, на которой могут быть и единицы (при наличии петель). Можно заметить, кроме того, количество единиц в MS* в точности равно количеству дуг (включая петли).
Слайд 30
Ориентированные графы (орграфы)
Связность орграфов бывает троякая:
- слабая;
-
односторонняя:
- сильная
Сильная связность означает взаимную достижимость любой пары вершин
«в обе стороны», т.е. с учетом ориентации дуг и в прямом, и в обратном направлении.
Односторонняя связность соответствует взаимной достижимости, по крайней мере, в одну сторону для любой пары вершин. При этом нет сильной связности.
Слайд 31
Ориентированные графы (орграфы)
Слабая связность определяется как связность только
на уровне неориентированного графа, получающегося из орграфа путем исключения
петель и стрелок (дуги превращаются в ребра).
Орграфу рис.22 соответствует обычный граф рис.1. и он связный, а орграф – слабосвязный.
Таким образом, слабая связность орграфа устанавливается на основании полной единичности матрицы связности «сопряженного» обычного графа.
При этом не должно быть ни односторонней, ни сильной связности орграфа.
Слайд 32
Ориентированные графы (орграфы)
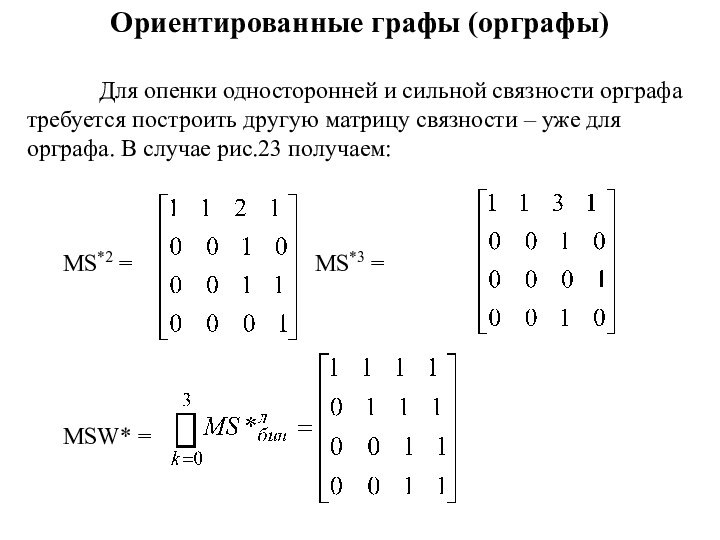
Для опенки односторонней и сильной связности
орграфа требуется построить другую матрицу связности – уже для
орграфа. В случае рис.23 получаем:
МS*2 = МS*3 =
MSW* =
Слайд 33
Ориентированные графы (орграфы)
Необходимое и достаточное условие сильной связности
орграфа – полная единичность его матрицы связности (MSW*).
Как видно,
в примере рис.23 орграф не сильносвязный.
Так, вершина 1 недостижима из всех остальных, вершина 2 – из вершин 3 и 4.
Так же очевидно и условие односторонней связности – в метках MSW*, симметричных относительно главной диагонали, должна быть хотя бы одна единица.
Это условие в примере выполнено.
Слайд 34
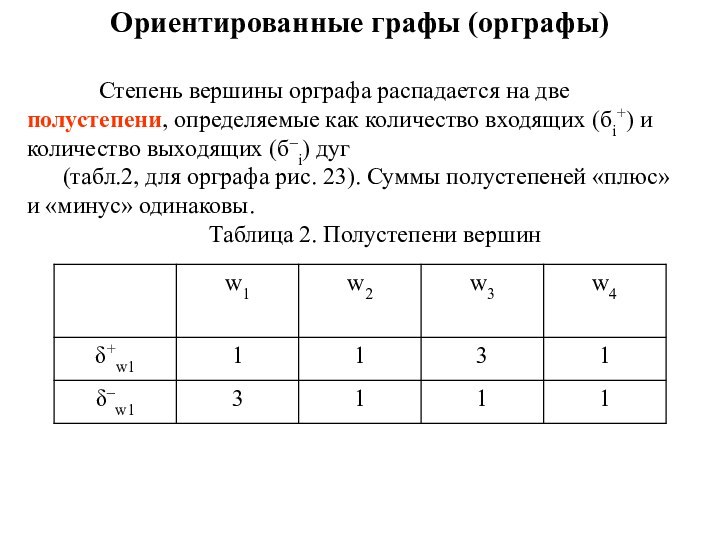
Ориентированные графы (орграфы)
Степень вершины орграфа распадается на две
полустепени, определяемые как количество входящих (бi+) и количество выходящих
(б–i) дуг
(табл.2, для орграфа рис. 23). Суммы полустепеней «плюс» и «минус» одинаковы.
Таблица 2. Полустепени вершин
Слайд 35
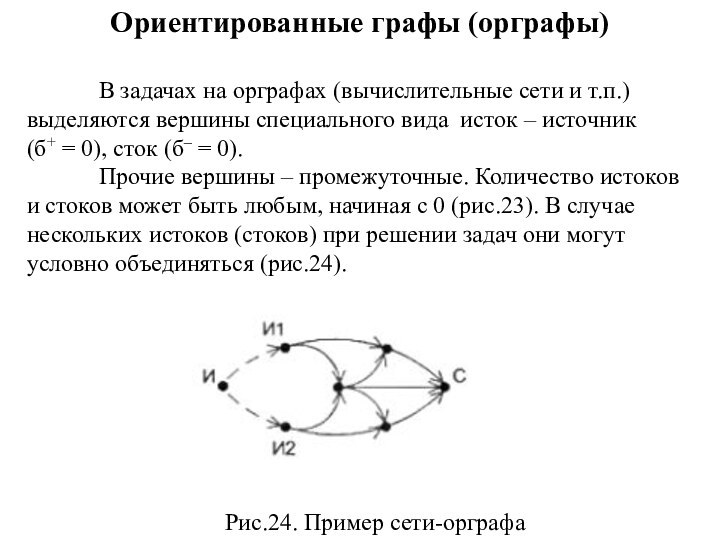
Ориентированные графы (орграфы)
В задачах на орграфах (вычислительные сети
и т.п.) выделяются вершины специального вида исток – источник
(б+ = 0), сток (б– = 0).
Прочие вершины – промежуточные. Количество истоков и стоков может быть любым, начиная с 0 (рис.23). В случае нескольких истоков (стоков) при решении задач они могут условно объединяться (рис.24).
Рис.24. Пример сети-орграфа
Слайд 36
Задачи на графах
Задачи на графах (на графовых моделях)
обычно очень сложно алгоритмизируются, а при решении требуют колоссальных
вычислительных ресурсов (машинной памяти и машинного времени).
Все такие зaдачи можно условно разделить на две группы:
маршруты, деревья и т.п.;
задачи с мерой.
В первой группе:
отыскание пути (маршрута) в лабиринте;
проверка графа на эйлеровость;
построение остовного дерева для связного графа;
ориентация графа;
…
Слайд 37
Задачи на графах
Алгоритмы для решения указанных выше задач
существуют, и даже во множестве.
Например, остовное дерево для
связного графа строится с использованием «поедающего» алгоритма – каждое ребро рассматривается всего один раз.
Оно оставляется («окрашивается») или удаляется. Удаляется, если с его участием образуется цикл. Практический смысл эта задача получает, например, когда речь идет о сети дорог (ребер), соединяющих населенные пункты (вершины). Наиболее экономичный вариант (в смысле стоимости дорог), очевидно, и соответствует остовному дереву – циклы вносят избыточность, поскольку остовное дерево уже связно. Конечно, здесь не учитываются затраты времени на дорожное сообщение (суммарная длина дорог и т.п.).
Слайд 38
Задачи на графах
Практический смысл имеет и задача ориентации
графа.
Здесь имеется в виду, что получающийся орграф – сильно-связный.
Тогда обеспечивается взаимная достижимость для любой пары вершин, причем в обе стороны. Это может означать, что в некотором, например, городе можно организовать одностороннее дорожное движение (вес виды транспорта двигаются в одном направлении; «встречной полосы» в принципе нет).
Оказывается, однако, не любой граф поддается такой ориентации.
Необходимое и достаточное условие для этого – каждое ребро должно входить хотя бы в один цикл.
Слайд 39
Задачи на графах
Задачи второй группы решаются на
помеченных графах.
Вот некоторые из таких задач:
минимальная связка;
кратчайший путь;
задача почтальона;
задача коммивояжера;
максимальный поток в сети;
поток с минимальной стоимостью;
транспортная задача с минимальной стоимостью;
транспортная задача с минимальным временем.
Слайд 40
Задачи на графах
Задача о минимальной связке (например, минимизируется
общая длина дорог) предполагает рассмотрение множества остовных деревьев (задача
3 из первой группы).
Задача почтальона заключается в построении замкнутого («от почты до почты») маршрута минимальной длины, проходящего по каждому ребру не менее одного раза. Похоже на попытку построения эйлерова цикла, но там прохождение по каждому ребру однократное.
Общий алгоритм решения задачи до сих пор не найден.
Слайд 41
Задачи на графах
Задача коммивояжера (разъездного торговца), также до
сих пор нерешенная (в общем случае), – построение замкнутого
маршрута минимальной длины, проходящего через каждую вершину (посещаемый с целью торговли населенный пункт, город) не менее одного раза.
Сходство с гамильтоновым циклом тоже условное, поскольку там прохождение через каждую вершину строго однократное. Рис. 6.25 показывает это различие – маршрут на рис.25а имеет длину 12 ед., а на рис. 25б – всего 4.
Рис.25. Частный случай решения задачи коммивояжера