Слайд 2
ИНФОРМАЦИЯ ОБ ОБЪЕКТАХ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ
может носить качественный
или количественный характер, и поэтому она может быть отнесена
к
классифицирующей (качественной),
топологической (сравнительной) и
метрической (количественной) информации.
Слайд 3
определяемая лишь качественно, служит для классификации объектов на
основе их общих характеристик.
Действия с классифицирующей информацией ограничиваются
только идентификацией объектов статистического исследования и отнесением этих объектов к тому или иному классу.
Классифицирующая информация,
Слайд 4
Топологическая информация
- это упорядоченная в соответствии с градациями
определенных свойств классифицирующая информация.
имеет большую познавательную ценность, поскольку она
позволяет не только устанавливать тождество между объектами, но и сравнивать их друг с другом, получая в результате их расположение в определённом порядке.
Слайд 5
Метрическая информация
не только выражает качественную характеристику объекта, но
и содержит точные и полные его количественные характеристики;
содержит
в себе и классифицирующую информацию, и топологическую информацию.
Слайд 6
Измерение информации
осуществляется с помощью различных шкал.
В
процессе измерения информации с помощью той или иной шкалы
отношения между объектами измерения отображаются на отношения между числами. И только после этого с информацией можно осуществлять какие-либо действия.
Слайд 7
Измерение
— это процедура, с помощью которой измеряемый объект
сравнивается с некоторым эталоном и получает числовое выражение в
определённом масштабе и шкале.
Здесь понятие «число» выступает в широком смысле и тем самым включает в себя возможность измерения всей совокупности типов информации.
Слайд 8
Тип шкалы
определяется соответствующим этой шкале множеством допустимых преобразований.
используются
четыре типа шкал: номинальная, порядковая, интервальная и метрическая шкалы.
Слайд 9
Каждая из шкал
определяется наличием или отсутствием четырех характеристик:
описание,
порядок,
расстояние,
начальная
точка.
Слайд 10
Описание шкалы
предполагает использование единого способа записи информации.
При
этом между элементами шкалы не вводится какая-либо характеристика сравнений
— осуществляется только идентификация информации.
Слайд 11
Порядок
характеризует наличие отношений в способах записи информации, наличие
крайних точек зрения.
При этом предусматриваются некоторые сравнительные характеристики, позволяющие,
например, упорядочить отношение к предмету исследования.
Слайд 12
Расстояние шкалы
может быть измерено. Это значит, что оно
существует только в тех шкалах, в которых элементы шкалы
определены количественно, а между этими элементами шкалы имеются интервалы, расстояние между которыми имеет смысловое значение.
Слайд 13
Начальная точка
задает тот или иной уровень соотношений между
элементами шкалы.
Слайд 14
Различные типы шкал
определяются в зависимости от наличия или
отсутствия четырёх характеристик, а также от способов их задания.
Слайд 15
Номинальная шкала
- это самая простая шкала.
обладает
только характеристикой описания — дается множество элементов, из которых
следует указать один элемент, причем не как результат сравнения, а как результат идентификации.
Данной шкале не присущи порядок, расстояние и начальная точка.
Слайд 16
Номинальная шкала
В качестве инструмента описания данной шкалы могут
выступать различные объекты — слова, словосочетания, набор букв, набор
цифр, символы, знаки, рисунки и т. п.
Слайд 17
Шкала порядка
уже имеет наряду с описанием еще
и порядок, в результате чего возможно установление приоритетов или
сравнений.
При этом шкала имеет тем или иным образом сформулированные ранги, определяющие степень предпочтения одного объекта другому.
Слайд 18
не позволяет давать толкование расстояниям между элементами шкалы,
поэтому эти элементы могут быть только сравнимы друг с
другом по рангам.
Это вызвано именно тем, что в шкалу порядка не вводится расстояние как элемент шкалы.
Шкала порядка
Слайд 19
Шкала интервалов
Может быть получена из шкалы порядка при
включении в нее расстояния как элемента шкалы.
В шкале интервалов
есть и описание, и порядок, и расстояние. Нет только одной характеристики — начальной точки.
Слайд 20
Шкалы расстояний
получаются из интервальных шкал при фиксации
единицы измерения.
При этом расстояние между близлежащими элементами шкалы является
величиной постоянной вне зависимости от того, на каком участке шкалы осуществляется сравнение.
возможны арифметические операции с числами на этой шкале.
Слайд 21
В метрической шкале
имеются все четыре характеристики, в том
числе и начальная точка, и эта шкала является наиболее
полной для целей обработки информации, например, шкала расстояний между телами, шкала веса тел, шкала стоимости товаров и т. п.
С элементами данной шкалы можно выполнять любые математические действия в полном объеме. Иногда эту шкалу называют «количественной шкалой» или «абсолютной шкалой».
Слайд 22
Ранжирование
представляет собой процедуру упорядочения альтернатив, выполняемую субъектом
управления, в результате которой поучается последовательность предпочтения вида:
а1 ⎬ a2 ⎬ … ⎬an (серия).
Слайд 23
Для серии
существует числовая система, элементами которой являются
числа, отношениям строго предпочтения соответствует в числовой системе отношения
строго больше.
Слайд 24
Ранжирование
для проведения ранжирования необходимо определить свойство, по
которому объекты упорядочиваются, то есть выявить основание ранжирования.
В порядке
осуществления процедуры упорядочения получается ранжированный ряд объектов ранжирования.
Слайд 25
Ранжирование
В этом ранжированном ряду каждому объекту приписывается
ранг — место в этом ряду. Число мест, как
и число рангов, равно числу объектов.
Слайд 26
Объекты ранжирования
могут быть либо все разными с точки
зрения выраженности в них заданного свойства, либо некоторые из
объектов ранжирования в рассматриваемой совокупности могут быть неразличимыми с точки зрения этого свойства.
Слайд 27
Связанные ранги
В первом случае все ранги ряда будут
различными, а во втором случае появятся одинаковые ранги у
нескольких объектов. Такие ранги называют связанными рангами.
Слайд 28
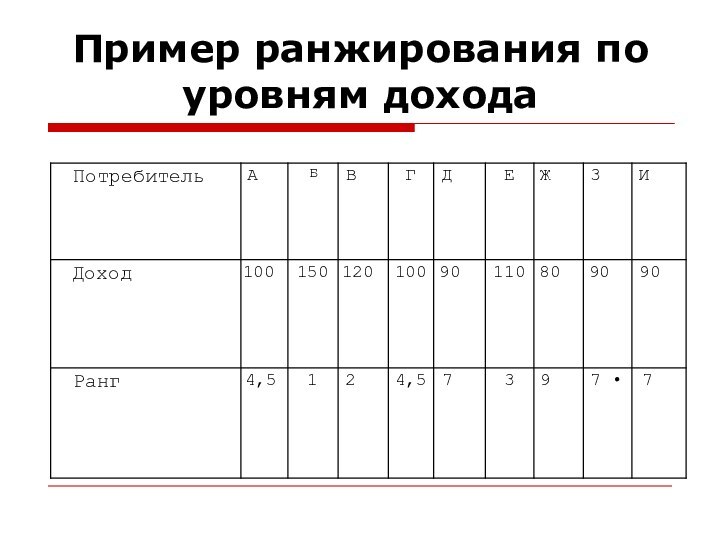
Пример ранжирования по уровням дохода
Слайд 29
Пример
На первом месте по рангу стоит гражданин, обозначенный
буквой Б —у него максимальный доход, равный 150 единицам.
На втором и третьих местах по уровням дохода стоят граждане, обозначенные буквами В и Е. У них проставлены соответствующие ранги 2 и 3.
Слайд 30
Пример
У граждан, обозначенных буквами А и Г одинаковые
доходы, а именно — по 100 денежных единиц у
каждого. Значит, они имеют одинаковые (связанные) ранги. Их ранг получается сложением мест (4+5) и делением этой величины на 2. В результате получилась величина 4,5.
Слайд 31
Пример
Граждане с доходом, равным 90 единиц, занимают шестое,
седьмое и восьмое места. Поэтому их ранг будет равен
величине (6+7+8)/3=7.
Слайд 32
Парное сравнение
– процедура установления предпочтения альтернатив при сравнении
всех возможных пар.
Слайд 33
Последовательность шагов
1. Каждый эксперт проводит попарную оценку приоритетности
признаков. При этом каждым экспертом заполняется матрица Еi=(Iikj ),
элементы которой в зависимости от выбора эксперта определяются по формуле:
1, если Xk ⎬ Xj или Xk ~ Xj;
Iikj = 0, если Xk ⎨ Xj.
Слайд 34
Последовательность шагов
2.Определяется сумма матриц всех экспертов.
3.Определяется результирующая
матрица R, каждый элемент которой вычисляется по формуле:
1, если z>=n/2
rkj =
0, если z<=n/2
Слайд 35
Последовательность шагов
4.Находится сумма баллов, которую набрал каждый признак.
Слайд 36
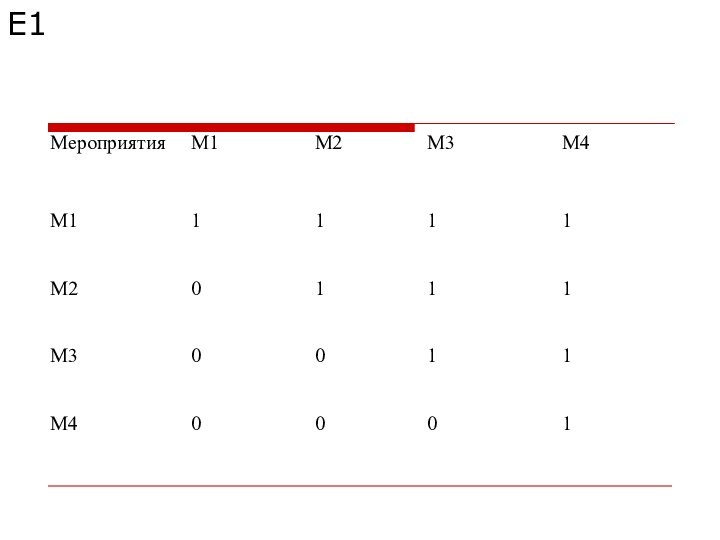
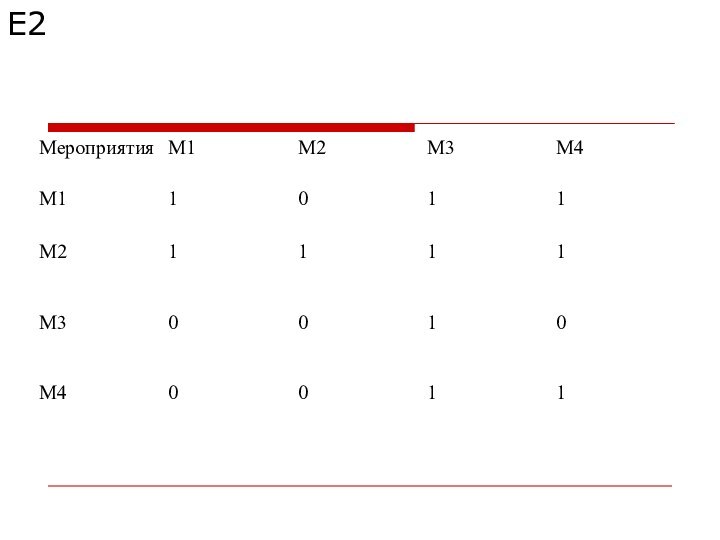
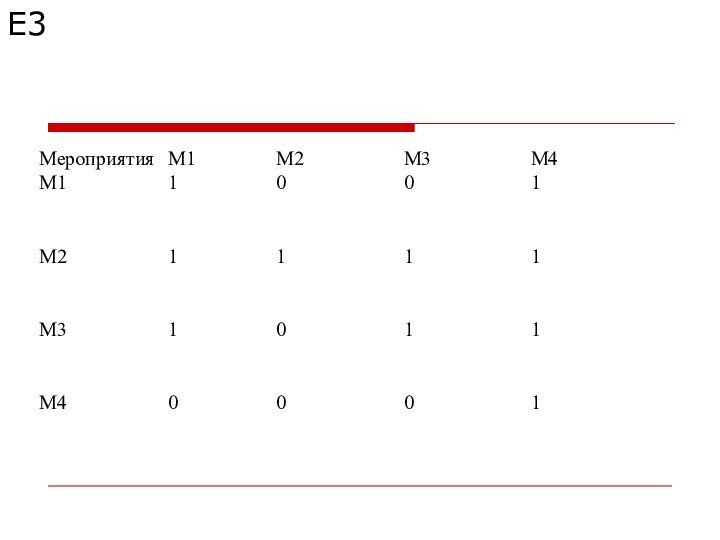
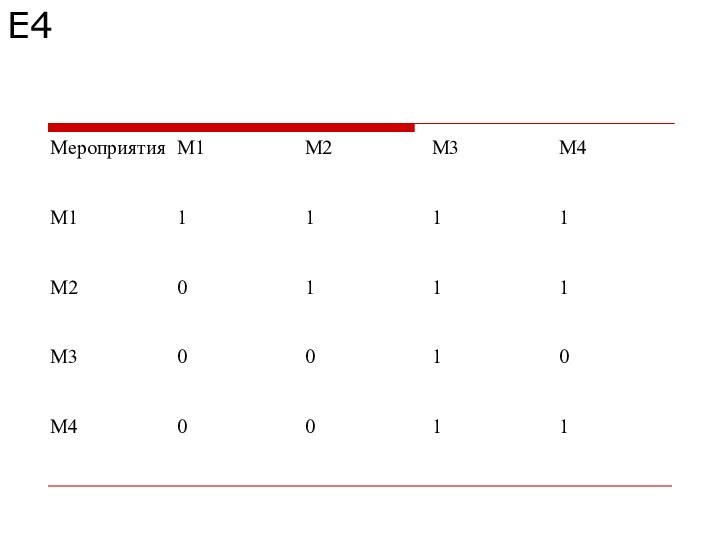
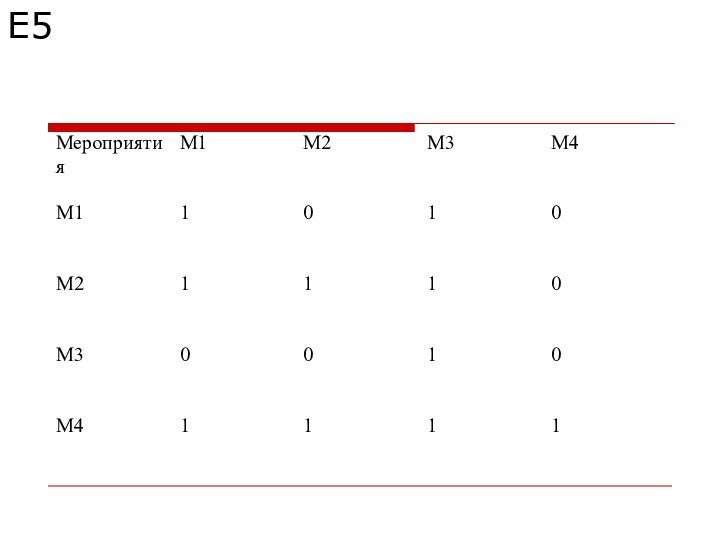
Пример
Для уменьшения выбросов вредных веществ в атмосферу на
заводе предлагается четыре альтернативных варианта фильтрации отходящих газов. Для
оценки этих вариантов была создана группа из пяти экспертов. Был использован метод парных сравнений. На основе парных сравнений альтернативных вариантов от каждого эксперта получены матрицы парных сравнений, показанные ниже.
Слайд 42
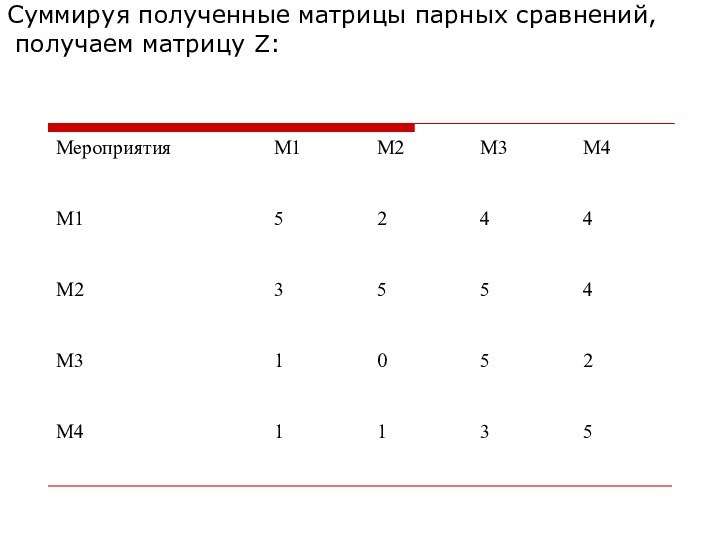
Суммируя полученные матрицы парных сравнений,
получаем матрицу Z:
Слайд 43
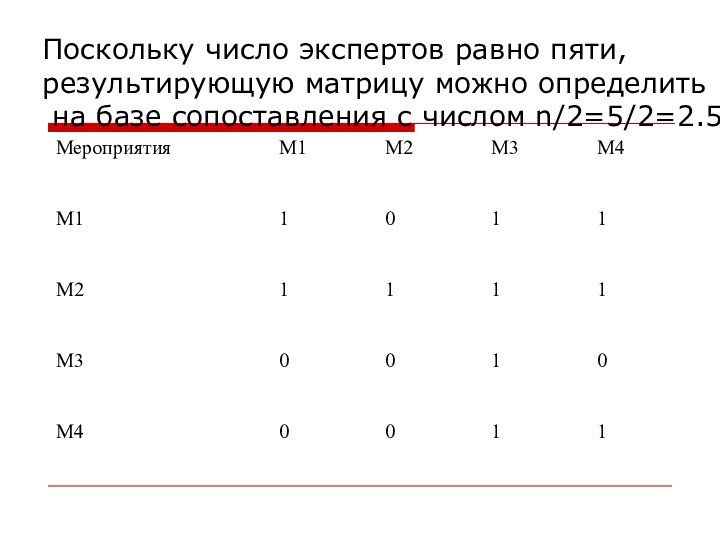
Поскольку число экспертов равно пяти,
результирующую матрицу можно
определить
на базе сопоставления с числом n/2=5/2=2.5.