Презентация на тему по инженерной графике на тему Геометрические построения

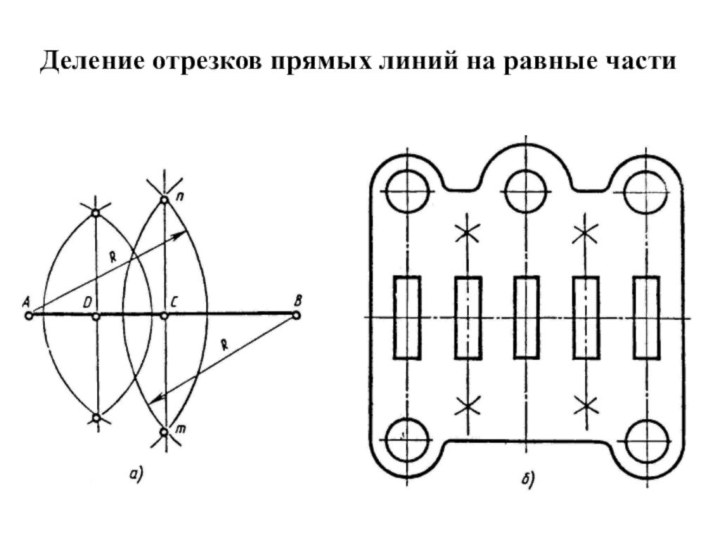
несколько большим половины отрезка, до взаимного пересечения в точках n и m. 

Через полученные точки  n и m проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части.
Проделав подобные построения для отрезков АС и СВ, получим точки, делящие отрезок АВ на четыре равные части.

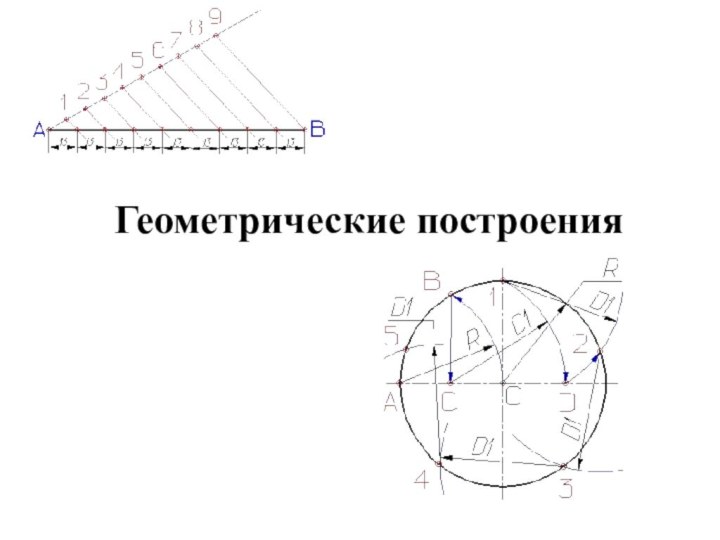
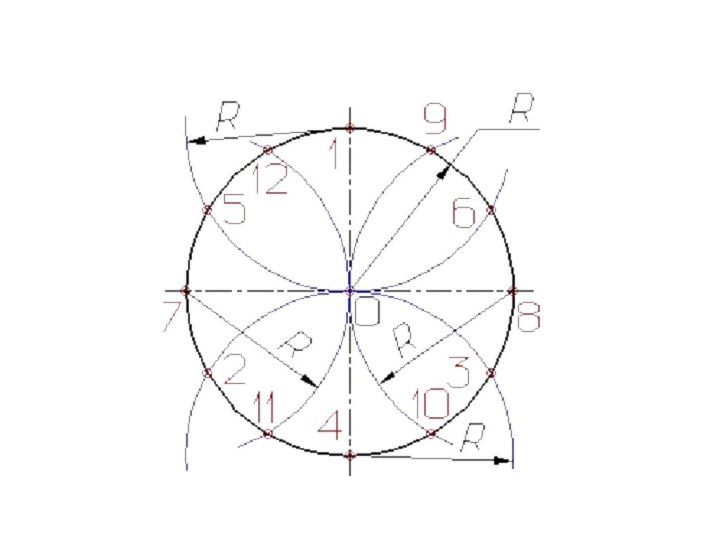
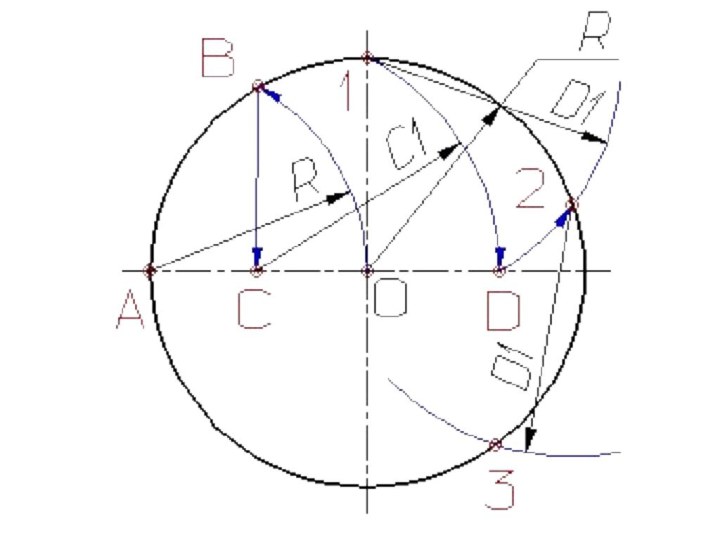
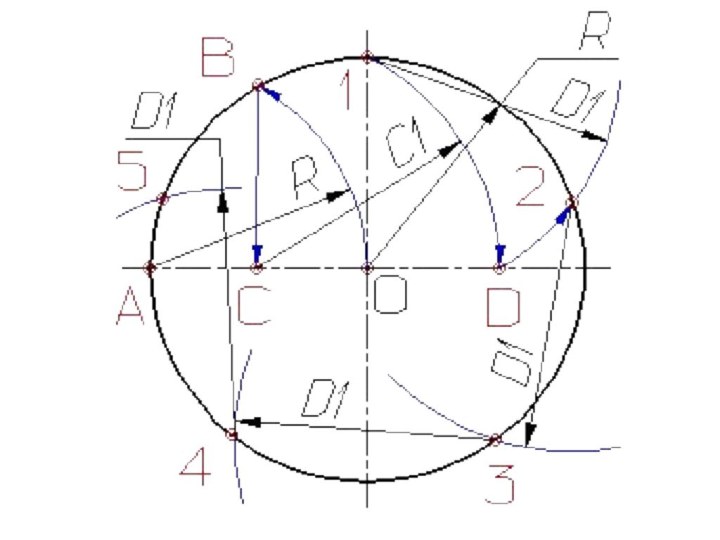
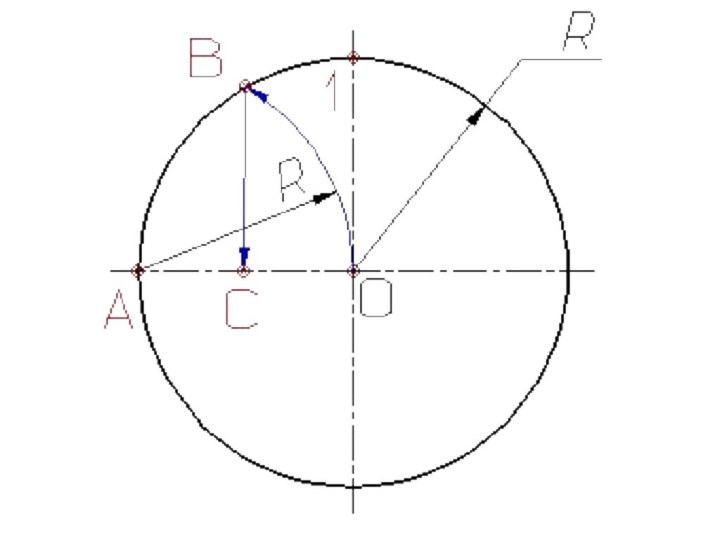
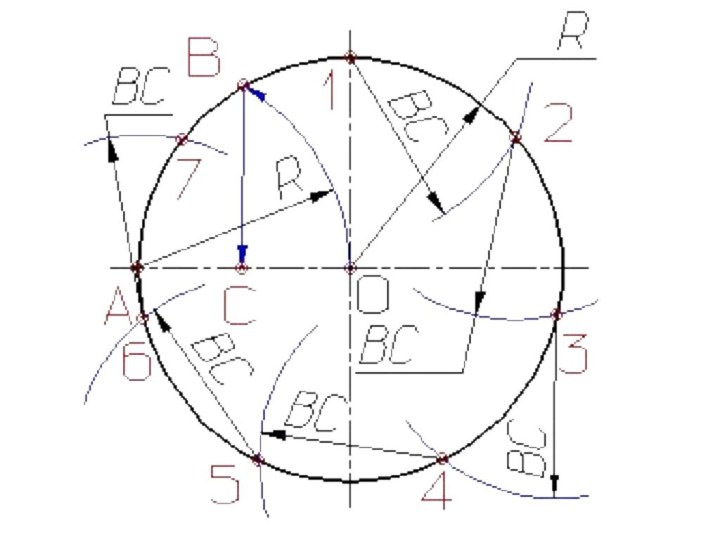
Деление отрезков прямых линий на равные части

пересечения со сторонами угла ВАС в точках n и

k. Из полученных точек проводят две дуги радиусом R, нескольким большим половины длины дуги nk, до взаимного пересечения в точке m. Вершину угла соединяют с точкой m прямой, которая делит угол пополам (биссектриса). Повторив это построение с углами Bаm и mAC угол ВАС можно разделить на четыре равные части

Деление угла на две и четыре равные части

выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности

произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги тем же радиусом R,  до взаимного пересечения пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

Деление прямого угла на три равные части

частей выполняется в следующей последовательности:
Выбираем в качестве точки 1,

точку пересечения осевой линии с окружностью
Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;
Точки 1, 2 и 3 делят окружность на три равные части;

проводим дугу радиусом равным радиусу окружности R до пересечения

с окружностью в точках 5 и 6;
Точки 1 - 6 делят окружность на шесть равных частей;
Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;
Точки 1 - 12 делят окружность на двенадцать равных частей.

частей

следующей последовательности:

Из точки А радиусом, равным радиусу окружности R,

проводим дугу, которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;
Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;
Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.

точки А радиусом, равным радиусу окружности R, проводим дугу,

которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7.

какое число n следует разделить окружность, находят по таблице

коэффициент k. При умножении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности n раз.

l=D×k